Objet exceptionnel

De nombreuses branches des mathématiques étudient des objets d'un certain type et démontrent à leur sujet un théorème de classification (en). Ces classifications produisent en général des suites infinies d’objets, et un nombre fini d’exceptions n’appartenant à aucune de ces suites, et connues sous le nom d’objets exceptionnels. Ces objets jouent souvent un rôle important dans le développement de la théorie, et les objets exceptionnels de divers domaines ont fréquemment des relations les uns avec les autres.

Polytopes réguliers[modifier | modifier le code]

Article principal : Polytope régulier.

Les premiers exemples d’objets exceptionnels proviennent de la classification des polytopes réguliers (convexes) : en deux dimensions, ils correspondent à la suite des polygones réguliers à n côtés (pour tout n ≥ 3) ; en toute dimension (supérieure à 2) il existe un analogue du cube, du tétraèdre régulier et de l’octaèdre régulier. À ces quatre suites s’adjoignent 5 polytopes exceptionnels : le dodécaèdre régulier et l’icosaèdre régulier en dimension 3, et, en dimension 4, le 120-cellules, le 600-cellules et le 24-cellules.

En incluant les polytopes non convexes, on rencontre une situation analogue : une suite infinie de polygones réguliers étoilés en dimension 2 (essentiellement, un pour chaque rationnel p/q< 1), et 14 objets exceptionnels, les quatre polyèdres de Kepler–Poinsot en dimension 3, et les 10 polychores de Schläfli-Hess en dimension 4 (il n'existe pas de polytopes réguliers non convexes en dimension supérieure à 4).

Ces résultats se généralisent aux pavages, en particulier aux pavages uniformes (en) de l'espace euclidien (les nids d'abeille) ou de l'espace hyperbolique. Il existe divers objets exceptionnels en dimension < 6 et une famille infinie de pavages du plan hyperbolique, mais à partir de la dimension 6, on ne rencontre que quatre familles de pavages (correspondant au simplexe, à l'hypercube, et à deux autres réseaux duaux des précédents).

Triangles de Möbius[modifier | modifier le code]

Les triangles de Möbius (en) sont des triangles qui pavent la sphère (plus généralement le plan euclidien ou le plan hyperbolique) par action du groupe du triangle (en) formé des réflexions autour de leurs côtés. En lien avec les polyèdres et les pavages exceptionnels discutés précédemment, on trouve sur la sphère 3 triangles de Möbius exceptionnels correspondant à l'octaèdre, au tétraèdre et à l'icosaèdre (ainsi qu'une famille infinie à un paramètre entier) ; de même, dans le plan euclidien, il n'existe que 3 triangles de Möbius, le triangle équilatéral, le triangle rectangle isocèle, et le demi-triangle équilatéral (les pavages correspondants sont représentés ci-contre).	(3 3 3)	(4 4 2)	(6 3 2)

Groupes simples finis[modifier | modifier le code]

Article principal : Groupe sporadique.

Relations entre les groupes sporadiques (la plupart sont reliés au groupe monstre).

Les groupes simples finis ont été classifiés en quatre familles infinies (groupes cycliques, alternés, classiques et de type de Lie) ; 26 groupes sporadiques n'appartiennent pas à ces familles. Parmi eux, 20 sont des sous-groupes ou des groupes quotients du groupe Monstre, connus sous le nom de « famille heureuse », tandis que les 6 autres sont appelés les « parias (en) ».

Plusieurs des groupes sporadiques sont liés au réseau de Leech, en particulier le groupe de Conway Co₁, qui est le quotient du groupe d'automorphismes du réseau par son centre.

Algèbres à division[modifier | modifier le code]

Il n'existe que trois algèbres à division associatives de dimension finie au-dessus des réels : les réels eux-mêmes, les nombres complexes et les quaternions ; de plus, la seule algèbre à division non associative est l'algèbre des octonions. Les octonions en particulier sont liés à une grande variété d'objets exceptionnels. Ainsi, l'unique algèbre de Jordan formellement réelle exceptionnelle est l'algèbre d'Albert des matrices 3x3 auto-adjointes sur les octonions.

Groupes de Lie simples[modifier | modifier le code]

Les groupes de Lie simples forment quatre suites (les groupes de Lie classiques) traditionnellement notées A, B, C et D. De plus, il existe 5 groupes exceptionnels : G₂ (le groupe d'automorphismes des octonions), F₄, E₆, E₇ et E₈. Les quatre derniers peuvent être vus comme les groupes de symétries de plans projectifs construits respectivement au-dessus de O, C⊗O, H⊗O et O⊗O, O notant les octonions et le produit tensoriel étant défini sur les réels.

La classification des groupes de Lie correspond à la classification des systèmes de racines, et donc les groupes de Lie exceptionnels correspondent à des systèmes de racines et à des diagrammes de Dynkin exceptionnels.

Algèbres supersymétriques[modifier | modifier le code]

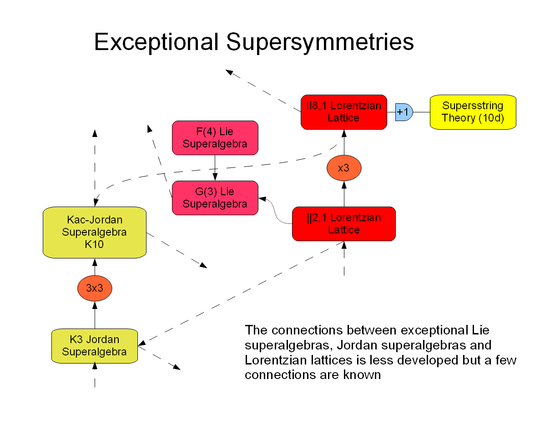
Quelques algèbres exceptionnelles sont munies de supersymétrie (en). En dimension finie, les principaux exemples sont les superalgèbres de Lie G(3) en dimension 31 et F(4) en dimension 40 , ainsi que les superalgèbres de Jordan K₃ et K₁₀.

Réseaux unimodulaires[modifier | modifier le code]

À isométrie près, il n'existe qu'un réseau unimodulaire (en) pair (c'est-à-dire dont toutes les normes sont paires) en dimension < 16 : le réseau E₈ (en) et, jusqu'en dimension 24, un seul réseau unimodulaire sans système de racines, le réseau de Leech. Trois des groupes sporadiques furent découverts par Conway en étudiant le groupe d'automorphismes du réseau de Leech : le groupe Co₁ est le groupe d'automorphismes lui-même modulo ±1 ; les groupes Co₂ et Co₃ (ainsi que d'autres groupes sporadiques), sont des stabilisateurs de divers sous-ensembles du réseau de Leech.

Codes[modifier | modifier le code]

Certains codes correcteurs peuvent être vus comme des objets exceptionnels, en particulier le code de Golay binaire parfait, qui est étroitement lié au réseau de Leech. Le groupe de Mathieu $M_{24}$ est quant à lui le groupe d'automorphismes du code de Golay binaire étendu.

Systèmes de blocs[modifier | modifier le code]

Parmi les systèmes de blocs exceptionnels figure le système de Steiner S(5,8,24) (connu aussi sous le nom de système de Witt), dont le groupe d'automorphismes est le groupe de Mathieu $M_{24}$ .

Automorphismes extérieurs[modifier | modifier le code]

Le groupe des automorphismes extérieurs (en) est défini comme le quotient du groupe des automorphismes par le groupe des automorphismes intérieurs ; certains automorphismes ne correspondant pas de manière canonique aux éléments de ce groupe sont dits exceptionnels.

Parmi les groupes simples finis, le seul exemple^[1] vient des automorphismes des groupes symétriques et alternés (en) : pour $3\leq n<6$ , le groupe alterné $A_{n}$ a un automorphisme extérieur (correspondant à la conjugaison par un élément impair de $S_{n}$ ), et le groupe symétrique $S_{n}$ n'en a aucun. Cependant, pour $n=6,$ il y a un automorphisme extérieur exceptionnel de $S_{6}$ (d'ordre 2), et le groupe des automorphismes extérieurs de $A_{6}$ n'est pas $C_{2}$ (le groupe à deux éléments) mais $C_{2}\times C_{2}$ (le groupe de Klein).

Si on considère A₆ comme le groupe linéaire projectif spécial (en) PSL(2,9), l'automorphisme extérieur n'est plus exceptionnel ; ainsi, le caractère exceptionnel vient de l'isomorphisme exceptionnel (en) $A_{6}\cong \operatorname {PSL} (2,9)$ , réalisé à l'intérieur du groupe de Mathieu M₁₂.

Les symétries du diagramme de Dynkin D₄ correspondent aux automorphismes extérieurs de Spin(8) (par trialité).

Parmi les groupes de Lie, le groupe spinoriel Spin(8) a un groupe des automorphismes extérieurs ( $S_{3}$ ) exceptionnellement grand, correspondant aux symétries exceptionnelles du diagramme de Dynkin D₄. Ce phénomène est connu sous le nom de trialité (en).

Les symétries exceptionnelles du diagramme D₄ donnent aussi naissance aux groupes de Steinberg.

Topologie algébrique[modifier | modifier le code]

Pour $n=2,6,14,30,62,$ et peut-être 126, mais aucune autre valeur, il existe des variétés parallélisables d'invariant de Kervaire (en) un ; ce sont des objets exceptionnels en rapport avec les sphères exotiques. On conjecture également l'existence de relations avec les plans projectifs de Rosenfeld (en) et avec certaines algèbres de Lie exceptionnelles, en raison des valeurs de ces dimensions, mais on n'en a encore déterminé aucune.

Relations avec les espaces de dimension 8 et 24[modifier | modifier le code]

De nombreuses relations ont été observées entre certains de ces objets exceptionnels, le plus souvent reliés aux dimensions 8 et 24. En revanche, et comme leur nom l'indique, les groupes parias (en) semblent isolés.

8 dimensions[modifier | modifier le code]

Les octonions sont de dimension 8.
Le réseau E₈ (en) a pour modèle les octonions entiers (à un facteur d'échelle près).
Les groupes de Lie exceptionnels peuvent être vus comme des groupes de symétries des octonions et de structures dérivées des octonions ; de plus, l'algèbre E₈ est reliée au réseau E₈ (comme l'implique la notation) : le réseau est engendré par le système de racines de l'algèbre.
La trialité se produit pour Spin(8).

24 dimensions[modifier | modifier le code]

Le réseau de Leech est de dimension 24.
La plupart des groupes simples sporadiques sont reliés au réseau de Leech, ou plus généralement au Monstre.
L'algèbre de Jordan exceptionnelle a une représentation en termes de matrices 24×24, munies du produit de Jordan.

Autres phénomènes[modifier | modifier le code]

Ces objets sont liés à de nombreux autres phénomènes mathématiques qui peuvent paraître surprenants, mais ne sont pas par eux-mêmes « exceptionnels ». Ainsi, en topologie algébrique, la périodicité de Bott (en) d'ordre 8 peut être vue comme provenant des octonions. Dans la théorie des formes modulaires, le fait que le réseau de Leech soit de dimension 24 est sous-jacent à la présence du nombre 24 dans les formules de la fonction êta de Dedekind et du discriminant modulaire, et cette connexion est renforcée par le « monstrous moonshine », reliant les fonctions modulaires au groupe Monstre.

En physique[modifier | modifier le code]

En théorie des cordes et en théorie des supercordes, il apparaît souvent des dimensions particulières nécessaires en raison d'un phénomène algébrique exceptionnel. Par exemple, la théorie des cordes bosoniques demande un espace-temps de dimension 26, ce qui a un lien direct avec l'apparition du nombre 24 dans la fonction êta de Dedekind. De même, les dimensions où est possible la supergravité sont liées aux dimensions des algèbres à division.

Objects non exceptionnels[modifier | modifier le code]

Pathologies[modifier | modifier le code]

Objects extrêmes[modifier | modifier le code]

Les objets d'une famille qui en sont l'exemple extrême pour une certaine mesure sont intéressants, mais non inhabituels au sens où les objets exceptionnels le sont. Par exemple, le nombre d'or φ possède la plus simple des approximations par une fraction continue, et est donc le plus difficile des réels à approcher par des rationnels ; mais il n'est nullement exceptionnel pour cette propriété.

De même, le triangle de Schwartz (2,3,7) est le plus petit triangle de Schwartz hyperbolique, et le groupe du triangle associé (en) est particulièrement intéressant, en tant que groupe de Hurwitz (en) universel et associé aux courbes de Hurwitz (en). Mais il appartient à une famille infinie de triangles ayant des propriétés analogues ((2,4,7), (2,3,8), (3,3,7), etc.), et n'est important que parce qu'il est le plus petit.

Relations entre physique et mathématique[modifier | modifier le code]

Beaucoup d'objets exceptionnels en mathématiques et en physique ont des liens entre eux. Ainsi, les conjectures connues sous le nom de « monstrous moonshine » montrent des liens entre le groupe Monstre et la théorie des cordes. La théorie des formes modulaires montre les liens entre E8 et le groupe Monstre. Le réseau de Leech, par l'intermédiaire du code de Golay, est lié à la matrice d'adjacence du dodécaèdre. La carte heuristique ci-dessous montre d'autres relations semblables.

Ces relations s'expliquent en partie en considérant ces objets comme formant un réseau d'algèbres vertex. Il se trouve que les algèbres vertex à la base de ce réseau sont si simples qu'elles sont isomorphes à des algèbres usuelles plus familières ; les relations sont ainsi de simples conséquences de ce que certaines algèbres sont en fait des sous-algèbres de certaines autres.

Supersymétries[modifier | modifier le code]

Les superalgèbres de Jordan sont un autre ensemble d'objets exceptionnels en lien avec la supersymétrie : ce sont les superalgèbres de Lie liées aux réseaux de Lorentz. Ce sujet étant moins développé que le précédent, les relations sont plus mal connues, mais il semble qu'on puisse formuler pour ces objets des conjectures analogues au monstrous moonshine mettant en jeu d'autres groupes sporadiques, comme le montre la carte heuristique ci-dessous.

Notes et références[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Exceptional object » (voir la liste des auteurs).

↑ ATLAS p. xvi

Voir aussi[modifier | modifier le code]

Articles connexes[modifier | modifier le code]

L'exception qui confirme la règle

Bibliographie[modifier | modifier le code]

(en) John Stillwell, « Exceptional Objects », American Mathematical Monthly,‎ novembre 1998, p. 850–858
(en) John Baez et John Huerta, Division Algebras and Supersymmetry II. « 1003.3436 », texte en accès libre, sur arXiv..
(en) This Week's Finds in Mathematical Physics, Week 106, John Baez
(en) Platonic Solids in all Dimensions, John Baez

Portail des mathématiques

[1] ATLAS p. xvi

[1]