Logarithme

Tracés des fonctions logarithmes en base 2, e et 10.

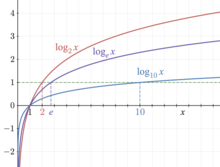
En mathématiques, le logarithme de base b d'un nombre réel strictement positif est la puissance à laquelle il faut élever la base b pour obtenir ce nombre. Par exemple, le logarithme de 1000 en base 10 est 3, car 1000 = 10×10×10 = 10³. Le logarithme de x en base b est noté log_b(x). Ainsi log₁₀(1000) = 3.

Tout logarithme transforme

• un produit en somme : $\log _{b}(x\cdot y)=\log _{b}x+\log _{b}y\,$
• un quotient en différence : $\log _{b}\left({\frac {x}{y}}\right)=\log _{b}x-\log _{b}y\,$
• une puissance en produit : $\log _{b}(x^{p})=p\log _{b}x.\,$

John Napier a développé les logarithmes au début du XVII^e siècle. Pendant trois siècles, les tables de logarithmes et les règles à calculs ont été utilisées pour réaliser des calculs, jusqu'à leur remplacement, à la fin du XX^e siècle, par des calculatrices.

Trois logarithmes sont remarquables :

• Le logarithme népérien (ou naturel), noté $\ln(x)$, qui utilise le nombre e comme base, est fondamental en analyse mathématique car il est la fonction réciproque de la fonction exponentielle ;
• Le logarithme décimal, qui utilise la base dix, était le plus communément utilisé pour les calculs ;
• Le logarithme binaire, qui utilise 2 comme base, est utile en informatique théorique et pour certains calculs appliqués.

Une échelle logarithmique permet de représenter sur un même graphique des nombres dont les ordres de grandeurs sont très différents. Les logarithmes sont fréquents dans les formules utilisées en sciences, mesurent la complexité des algorithmes et des fractales et apparaissent dans des formules permettant de compter les nombres premiers. Ils décrivent les intervalles musicaux ou certains modèles de psychophysique.

Le logarithme complexe est la fonction réciproque de l'exponentielle complexe et généralise ainsi la notion de logarithme aux nombres complexes. Le logarithme discret généralise les logarithmes aux groupes cycliques et a des applications en cryptographie à clé publique.

Historique

Vers la fin du XVI^e siècle, le développement de l'astronomie et de la navigation d'une part et les calculs bancaires d'intérêts composés d'autre part, poussent les mathématiciens à chercher des méthodes de simplifications de calculs et en particulier le remplacement des multiplications par des sommes. Utilisant les tables trigonométriques, les mathématiciens Paul Wittich (1546—1586) et Christophe Clavius (dans son traité de Astrolabio) établissent des correspondances entre produit ou quotient d'une part et somme, différence et division par deux d'autre part, pour des nombres inférieurs à 1 à l'aide de relations trigonométriques. Par exemple en posant x = sin(a) et y = cos(b) on peut formuler :

$x\times y=\sin(a)\times \cos(b)={\frac {\sin(a-b)+\sin(a+b)}{2}}.$

C'est la méthode dite de prosthaphaeresis [du grec προσθαφαίρεσις formé par contraction à partir des deux mots grecs πρόσθεσις (application, addition) et ἀϕαίρεσις (enlèvement, abstraction, soustraction)] qui est avantageusement remplacée quelques années plus tard par les tables logarithmiques.

Simon Stévin, intendant général de l'armée hollandaise, met au point des tables de calculs d'intérêts composés. Ce travail est poursuivi par Jost Bürgi qui publie en 1620, dans son Aritmetische und geometrische Progress-tabulen, une table de correspondance entre n et 1,0001ⁿ. À une somme dans la première colonne correspond ainsi un produit dans la seconde colonne.

En 1614, John Napier (ou Neper) publie son traité Mirifici Logarithmorum Canonis Descriptio. Il ne songe pas qu’il est en train de créer de nouvelles fonctions, mais seulement des tables de correspondances (logos = rapport, relation, arithmeticos = nombre) entre deux séries de valeurs possédant la propriété suivante : à un produit dans une colonne correspond une somme dans une autre. Ces tables de correspondances ont été créées initialement pour simplifier les calculs trigonométriques apparaissant dans les calculs astronomiques et seront utilisées quelques années plus tard par Kepler. La notation Log comme abréviation de logarithme apparaît en 1616 dans une traduction anglaise de l'œuvre de Neper. En 1619, apparaît une œuvre posthume de Neper Mirifici Logarithmorum Canonis Constructio, où il explique comment construire une table de logarithmes.

Son travail sera poursuivi et prolongé par le mathématicien anglais Henry Briggs qui publie en 1624 ses tables de logarithmes décimaux (Arithmetica logarithmica) et précise les méthodes d’utilisation des tables pour calculer des sinus, retrouver des angles de tangente... Le logarithme décimal est parfois appelé logarithme de Briggs en son honneur. La même année, Johann Kepler publie Chilias logarithmorum construites en utilisant un procédé géométrique. La table de Briggs présente les logarithmes à 14 chiffres des nombres compris entre 1 et 20 000 et entre 90 000 et 100 000. Son travail est complété par Ezechiel de Decker et Adriaan Vlacq qui publient en 1627 une table de logarithmes complète.

En 1647, lorsque Grégoire de Saint-Vincent travaille sur la quadrature de l’hyperbole, il met en évidence une nouvelle fonction qui se trouve être la primitive de la fonction $x\mapsto {\tfrac {1}{x}}$ s’annulant en 1 mais c’est Huygens en 1661 qui remarquera que cette fonction se trouve être une fonction logarithme particulière : le logarithme naturel.

La notion de fonction, la correspondance entre les fonctions exponentielles et les fonctions logarithmes n’apparaissent que plus tardivement après le travail de Leibniz sur la notion de fonction (1697).

Propriétés des fonctions logarithmes de base a

Propriétés algébriques

Les fonctions logarithmes sont par définition les morphismes continus non constamment nuls de $(\mathbb {R} _{+}^{*},\times )$ vers $(\mathbb {R} ,+)$.

Pour tout réel a strictement positif et différent de 1, le logarithme de base a : log_a est la fonction continue définie sur $\mathbb {R} _{+}^{*}$ vérifiant l'équation fonctionnelle :

pour tous x et y réels strictement positifs,

$\log _{a}(xy)=\log _{a}(x)+\log _{a}(y)$

et

$\log _{a}(a)=1$

Cette définition permet de déduire rapidement les propriétés suivantes

$\log _{a}(1)=0$

$\log _{a}(x/y)=\log _{a}(x)-\log _{a}(y)$

$\log _{a}(x^{n})=n\log _{a}(x)$

$\log _{a}(a^{n})=n$ pour tout entier naturel n, puis pour tout entier relatif n

$\log _{a}(a^{r})=r$ pour tout rationnel r.

Comme tout réel strictement positif x est la limite d'une suite dont le terme général est de la forme a^r_n, où (r_n) est une suite de rationnels convergeant vers un réel $\ell$, on détermine log_a(x) comme étant la limite de r_n.

Proportionnalité

Deux fonctions logarithmes ne diffèrent que d’une constante multiplicative : pour tous réels strictement positifs différents de 1, a et b, il existe un réel k tel que :

$\log _{b}=k\log _{a}$.

Ce réel k vaut ${\frac {1}{\log _{a}(b)}}$.

En effet $\log _{b}$ est la fonction continue qui transforme un produit en somme et qui vaut 1 en b, mais, pour tout réel k non nul, la fonction k log_a est aussi une fonction continue, non constante qui transforme un produit en somme et cette fonction vaut 1 en b si et seulement si :

$k={\frac {1}{\log _{a}(b)}}$.

Toutes les fonctions logarithmes peuvent donc s’exprimer à l’aide d’une seule, une dont on connaît déjà la dérivée : la fonction logarithme népérien. Pour tout réel a strictement positif et différent de 1, et pour tout réel x strictement positif, on a :

$\log _{a}(x)={\frac {\ln(x)}{\ln(a)}}$.

Dérivée

La fonction log_a est dérivable sur $\mathbb {R} _{+}^{*}$ de dérivée :

$\log _{a}'(x)={\frac {1}{x\ln(a)}}$ qui a même signe que ln(a).

Donc la fonction log_a est strictement monotone, croissante quand a est supérieur à 1, décroissante dans le cas contraire.

Fonction réciproque (antilogarithme)

Représentation dans le cas b > 1. Le graphe de la fonction logarithmique log_b(x) (bleu) est obtenu en reflétant celui de la fonction b^x (rouge) par rapport à la diagonale x = y.

La fonction $\log _{a}:\mathbb {R} _{+}^{*}\to \mathbb {R}$ est une bijection dont la bijection réciproque est la fonction $\operatorname {antilog_{a}} :\mathbb {R} \to \mathbb {R} _{+}^{*}\equiv x\mapsto a^{x}$.

Autrement dit, les deux façons possibles de combiner (ou composer) les logarithmes et l’élévation à des puissances redonnent le nombre original :

• pour tout réel x, prendre la puissance x-ième de a, puis le logarithme en base a de cette puissance, redonne x :$\forall x\in \mathbb {R} _{+}^{*}\quad \log _{a}(a^{x})=x\log _{a}(a)=x~;$
• inversement, pour tout réel y strictement positif, prendre d'abord le logarithme, puis élever a à sa puissance, redonne y :$a^{\log _{a}(y)}=y.$

Les fonctions réciproques sont étroitement liées aux fonctions originales. Leurs graphes, qui se correspondent lorsqu’on échange les coordonnées x et y (ou par réflexion par rapport à la diagonale x = y), sont montrés à droite dans le cas où a est un réel b strictement supérieur à 1 : un point (u, t = b^u) sur le graphe (rouge) de la fonction antilogarithme x ↦ b^x fournit un point (t, u = log_b(t)) sur le graphe (bleu) du logarithme et vice versa. Comme b > 1, la fonction log_b est croissante et quand x tend vers +∞, log_b(x) tend vers +∞, tandis que lorsque x approche zéro, log_b(x) tend vers –∞. Dans le cas où le réel a est strictement compris entre 0 et 1, la fonction log_a est décroissante et ces limites sont interverties.

En matière de calcul, l'antilog ramène des logarithmes aux valeurs. Soit à évaluer une formule F combinant multiplications, divisions et exponentiations, et soit f la formule définissant le logarithme de F en combinant sommes, différences et produits des (logarithmes) des données. La valeur de F peut s'obtenir comme l'antilog de la valeur de f, ce qui conclut le calcul. On peut ainsi remplacer l'évaluation $F=(x\times y\times z)^{1/3}$

par

$F=\operatorname {antilog_{a}} ((\log _{a}(x)+\log _{a}(y)+\log _{a}(z))/3)$.

Fonctions logarithme courantes

Logarithme népérien

Le logarithme népérien, ou logarithme naturel, est la fonction logarithme dont la dérivée est la fonction inverse définie de $\mathbb {R} _{+}^{*}$ dans $\mathbb {R}$ : $x\mapsto {\frac {1}{x}}$.

La fonction de Neper est par convention notée « log » ou « ln », la première notation étant cependant encore couramment utilisée en théorie des nombres et en informatique.

La base de la fonction logarithme népérien, notée e, est appelée nombre de Néper ou nombre d'Euler.

Sa valeur approchée est :

$\mathrm {e} \approx 2{,}718\,281\,828\,459\,045\,235\,360\ldots$.

Logarithme décimal

C’est le logarithme le plus pratique dans les calculs numériques manuels, il est noté log ou log₁₀. La norme ISO 80000-2 indique que log₁₀ devrait être noté lg, mais cette notation est rarement utilisée.

On le retrouve dans la création des échelles logarithmiques, les repères semi-logarithmiques ou log-log, dans la règle à calcul, dans le calcul du pH, dans l’unité du décibel.

Il précise à quelle puissance il faut élever 10 pour retrouver le nombre de départ : l'image d'un nombre par log est l'entier relatif auquel il faut élever 10 pour obtenir l'antécédent. Par exemple :

En base 10 :

$\log _{10}(10)=1{\text{ car }}10^{1}=10$

$\log _{10}(100)=2{\text{ car }}10^{2}=100$

$\log _{10}(1000)=3{\text{ car }}10^{3}=1000$

$\log _{10}(0,01)=-2{\text{ car }}10^{-2}=0,01$

La valeur du logarithme d’autres nombres que des puissances de 10 demande un calcul approché. Le calcul de log(2) par exemple peut se faire à la main, en remarquant que 2¹⁰ ≈ 1000 donc 10 log₁₀(2) ≈ 3 donc log₁₀(2) ≈ 0,3.

On note la relation : $\log _{10}(x)={\frac {\ln(x)}{\ln(10)}}$ (la fonction ln étant le logarithme népérien).

Logarithme binaire

La norme ISO 80 000 recommande de noter lb le logarithme en base 2.

Le logarithme binaire, d'usage spécialisé dans le calcul des intervalles musicaux en cents ou en savarts, a trouvé beaucoup plus d'application en informatique. Les ordinateurs travaillant en système binaire, le calcul d'un logarithme en base 2 se fait par l'algorithme le plus précis et le plus efficace.

Un nombre x codé en virgule flottante binaire se décompose en une mantisse m, comprise entre 1 (inclus) et 2 (exclu) et un exposant p, indiquant la puissance de 2 qui multiplie la mantisse pour obtenir le nombre. L'exposant est la partie entière du logarithme binaire, tandis que le logarithme binaire de la mantisse est compris entre 0 (inclus) et 1 (exclu).

$x=2^{p}\times m\Longrightarrow {\textrm {lb}}(x)=p+{\textrm {lb}}(m).$

Ce qui ramène le calcul à celui du logarithme binaire d'un nombre entre 1 (inclus) et 2 (exclu). Si on multiplie ce nombre par lui-même, et que le résultat dépasse 2, c'est que le nombre est supérieur à √2: la chiffre suivant, après la virgule est un 1, dans le cas contraire, c'est un 0. On continue par itération jusqu'à la précision souhaitée.

Ce logarithme est lié aux autres logarithmes, par :

$\ln(x)={\frac {\mathrm {lb} (x)}{\mathrm {lb} (e)}}{\text{ et }}\log(x)={\frac {\mathrm {lb} (x)}{\mathrm {lb} (10)}}.$

Cologarithme

Le cologarithme d'un nombre est le logarithme de l'inverse de ce nombre. C'est une notion courante en chimie pour l'opérateur pX (dont le pH).

Voir aussi

Articles connexes

• Logarithme naturel
• Logarithme décimal
• Logarithme binaire
• Antilogarithme
• Cologarithme
• Logarithme complexe
• Fonction polylogarithme
• Fonction holomorphe
• Fonction exponentielle
• Loi de Benford

• Acoustique musicale : Intervalles sonores et logarithmes

Applications pratiques

• Règle à calcul
• Échelle logarithmique
• Table de logarithmes

Lien externe

Simone Trompler, Histoire des logarithmes, publié en ligne en 2002 par l’Université libre de Bruxelles