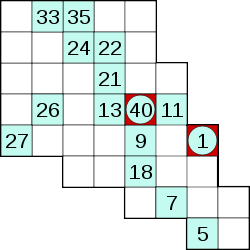
Hidato
Hidato désigne un jeu de puzzle logique inventé par Gyora Benedek, un mathématicien israélien.
Dans le Hidato, une grille avec des cases blanches et des noires est donnée. En utilisant autant de cases noires que nécessaire, on peut donner à la grille effective (les cases blanches) à peu près n'importe quelle forme.
Le but du jeu est de remplir les cases blanches avec des nombres consécutifs qui suivent un chemin continu sur cette grille, selon la relation de voisinage immédiat (le long des horizontales, des verticales et des diagonales) - et qui sont, bien entendu, compatibles avec les nombres déjà donnés.
Le plus petit nombre (en principe 1) et le plus grand nombre sont en principe (mais pas toujours) donnés. Des nombres intermédiaires peuvent également être donnés.
À propos du puzzle[modifier | modifier le code]
Des puzzles de Hidato sont publiés dans des journaux comme le Daily Mail et le Detroit Free Press.
Un puzzle de Hidato bien formé est censé avoir une solution unique. De plus, un puzzle de Hidato destiné à des joueurs humains devrait être résoluble par des règles logiques plus ou moins simples. Cependant, il existe des puzzles de Hidato très durs, même de petite taille.
Un puzzle voisin du Hidato est le Numbrix, inventé par Marilyn Vos Savant. Le but du Numbrix est le même que dans le Hidato, sauf que les déplacements selon les diagonales ne sont pas autorisés.
Il semble que les noms Numbrix and Hidato soient des marques déposées.
Techniques de résolution[modifier | modifier le code]
Comme pour beaucoup de puzzles logiques, la technique de résolution de base consiste à analyser les possibilités pour chaque nombre d'être présent dans chaque case blanche. Quand une case blanche contient un seul nombre possible (Naked Single) ou quand un nombre a une seule place possible (Hidden Single), on peut être sûr qu'il appartient à la solution.
Toutefois, comme dans le cas du Sudoku, la résolution des puzzles de Hidato ou de Numbrix plus durs requiert l'utilisation de techniques plus complexes - en particulier divers types de chaînes.
Un livre récent en anglais Pattern-Based Constraint Satisfaction and Logic Puzzles[1] montre que les techniques développées pour le Sudoku dans un livre plus ancien du même autheur The Hidden Logic of Sudoku[2] se généralisent à n'importe quel problème fini de Satisfaction de Contraintes. Cela inclut les chaînes xy, les fouets (whips) et les tresses (braids). Ce livre montre aussi en détail comment appliquer ces chaînes aux puzzles de Hidato et de Numbrix.
Implémentant les techniques définies dans le livre ci-dessus, le logiciel général de résolution à base de règles pour les problèmes de Satisfaction de Contraintes (CSP-Rules) contient une partie spécifique pour le jeu de Numbrix et Hidato (HidatoRules). Il est librement disponible dur la plateforme GitHub: https://github.com/denis-berthier/CSP-Rules-V2.1
Notes et références[modifier | modifier le code]
- (en) Denis Berthier, « Pattern-Based Constraint Satisfaction and Logic Puzzles », Lulu Publishers, (ISBN 978-1-291-20339-4), (lire en ligne, consulté le )
- (en) Denis Berthier, « The Hidden Logic of Sudoku », Lulu Publishers, (ISBN 978-1-84753-472-9), (lire en ligne, consulté le )