Heptagone

Heptagone régulier


Type	Polygone régulier
Arêtes	7
Sommets	7

Symbole de Schläfli	{7}
Groupe de symétrie	Groupe diédral D₁₄
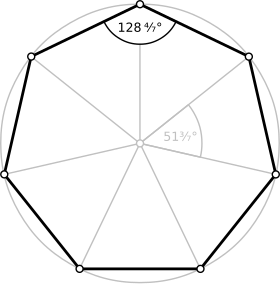
Angle interne	128°⁴⁄₇
modifier

Un heptagone est un polygone à sept sommets, donc sept côtés et quatorze diagonales.

La somme des angles internes d'un heptagone non croisé vaut $5π$ radians.

Un heptagone régulier est un heptagone dont tous les côtés sont égaux et dont tous les angles internes sont égaux. Il y en a trois : deux étoilés (les heptagrammes réguliers) et un convexe. C'est de ce dernier qu'il s'agit lorsqu'on parle de « l'heptagone régulier ».

L'heptagone régulier est le plus petit des polygones réguliers non constructibles à la règle et au compas. Il est cependant possible de réaliser une construction à la règle et au compas si l'on s'aide d'autres outils géométriques ou si la règle peut être graduée (construction par neusis). Il est aussi possible d'en tracer une version approchée, aux erreurs faibles, avec le compas et la règle non graduée.

Caractéristiques de l'heptagone régulier[modifier | modifier le code]

Les angles internes sont tous égaux à $5π/7$ rad.
Les angles au centre sont tous égaux à $2π/7$ rad.
Si le côté a pour longueur a :
- le rayon $r$ du cercle circonscrit est égal à $r={\frac {a}{2\sin \left({\frac {\pi }{7}}\right)}}\approx 1{,}15238~a$ ;
- le rayon $r i$ du cercle inscrit est égal à $r_{i}={\frac {a}{2}}\cot \left({\frac {\pi }{7}}\right)$ ;
- l'aire est égale à ${\frac {7}{4}}~a^{2}\cot \left({\frac {\pi }{7}}\right)\approx 3{,}63391~a^{2}$ .

Non-constructibilité par règle et compas[modifier | modifier le code]

L'heptagone régulier n'est pas constructible à la règle et au compas car le nombre premier 7 n'est pas un nombre de Fermat (théorème de Gauss-Wantzel). On peut aussi démontrer cette propriété de non-constructibilité sans faire appel aux nombres de Fermat, en utilisant seulement le théorème de Wantzel :

Article connexe : Polynôme minimal des valeurs spéciales trigonométriques.

Notons $a = 2 k π / 7$ et $x = cos a$ . Si l'heptagone était constructible alors $x$ serait un nombre constructible. Les angles $3 a$ et $4 a$ ayant pour somme $2 k π$ , on a

\cos(4a)=\cos(3a)

qui, par les formules d'angle multiple, se réécrit

8x^{4}-8x^{2}+1=4x^{3}-3x

ou encore

(x-1)(8x^{3}+4x^{2}-4x-1)=0

.

Pour $k$ non multiple de 7, le réel $x$ est donc racine de $8 x 3 + 4 x 2 - 4 x - 1$ , qui est irréductible sur $\mathbb {Q}$ et de degré 3. Ceci est en contradiction avec le résultat établi par Wantzel, qui énonce que le polynôme minimal d'un nombre constructible a toujours pour degré une puissance de 2. Donc $cos a$ n'est pas constructible si $k$ n'est pas multiple de 7, par conséquent l'heptagone n'est pas constructible.

Construction par intersection de coniques[modifier | modifier le code]

L'heptagone est cependant constructible à l'aide de coniques, puisque^[1] 7 est premier de la forme $2 α 3 β + 1$ , ou encore : puisque^[2] l'heptagone est constructible par neusis (voir infra).

La figure jointe^[3] offre une construction de l'heptagone à l'aide du cercle unité et d'une hyperbole équilatère de centre $Ω(1/4, \sqrt 7 /4)$ et passant par $A (1, 0)$ . Dans cette construction, quatre des sept sommets apparaissent comme points d'intersection du cercle circonscrit et de cette hyperbole équilatère, d'équation :

y={\frac {{\sqrt {7}}\pm {\sqrt {(4x-1)^{2}-2}}}{4}}

.

Construction par neusis[modifier | modifier le code]

Une construction par neusis ou par inclinaison est un procédé de construction utilisant une règle graduée et consistant à construire un segment de longueur donnée dont les extrémités se trouvent sur deux courbes données. Il s'agit ici de construire un angle de $π/7$ .

Une construction préliminaire[modifier | modifier le code]

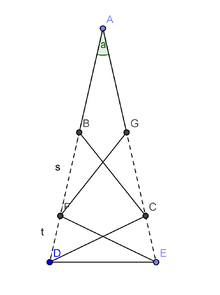
Dans la figure jointe, ABCDEFGA est un polygone où tous les segments sont de longueur 1. ABFD sont alignés et AGCE aussi.

On prouve que l'angle DAE vaut $π/7$ :

on note cet angle

a

, qui est également l'angle BAC

le triangle ABC étant isocèle, l'angle opposé ACB vaut

a

lui aussi ;

la somme des angles d'un triangle vaut

π

, l'angle ABC vaut

π - 2 a

et l'angle complémentaire CBD vaut

2 a

;

le triangle BCD étant isocèle, l'angle opposé CDB a également la même valeur (

2 a

) et l'angle BCD vaut

π - 4 a

;

la somme des angles ACB (qui vaut

a

), BCD (

π - 4 a

) et DCE vaut

π

, donc DCE vaut

3 a

.

Le triangle CDE étant isocèle, l'angle opposé DEC vaut lui aussi

3 a

; l'angle DEA est le même.

Le triangle ADE étant isocèle, c'est aussi la valeur de l'angle EDA, et la somme des angles vaut

7 a

, mais aussi

π

donc

a = π/7

.

On prouve que la longueur BE vaut √2 :

On note

s

et

t

les longueurs BF et FD.

Le triangle FDE étant isocèle,

2 cos(EDF) = t

.

Les droites (FC) et (DE) étant parallèles, l'angle ACF vaut

3 a

. Comme l'angle ACB vaut

a

, l'angle BCF vaut

3 a - a = 2 a

. Le triangle BFC est donc isocèle et FC = FB =

s

Le même parallélisme permet de dire, d'après le théorème de Thalès, que

{\frac {1+s}{1+s+t}}={\frac {s}{1}}

qui, par produit en croix et simplification, donne

s 2 + st = 1

.

Le théorème d'Al-Kashi dans le triangle BDE donne alors

BE^{2}=BD^{2}+DE^{2}-2.BD.DE.\cos(EDF)=1+(s+t)^{2}-t(s+t)=1+s^{2}+st=2

.

La construction par neusis[modifier | modifier le code]

Il s'agit de construire un point A sur la médiatrice d'un segment [DE] et un point B sur le segment [AD] tels que AB = 1 et BE = √2. On aura alors reconstitué le triangle précédent.

On construit un carré CDEF de côté 1, on trace la médiatrice (d) de [DE], et aussi de [CF], ainsi que le cercle de centre E et de rayon EC.

On place l'origine de la règle sur la médiatrice, la règle s'appuie sur le point D, on fait glisser le long de la médiatrice l'origine de la règle vers le haut de la figure tout en conservant l'appui sur D, jusqu'à ce que le cercle (C) traverse la règle à la graduation 1. On obtient alors les points B et A aux graduations 0 et 1 respectivement.

On construit le cercle circonscrit au triangle isocèle ADE (par la méthode de l'intersection des médiatrices de deux de ses côtés, qui détermine le centre O du cercle à construire, le positionnement le plus précis étant de prendre les deux côtés les plus longs qui doit aussi coïncider sur la médiatrice déjà tracée (d) de DE), qui se trouve être aussi le cercle circonscrit de l'heptagone DEGHAIJ de base DE, qu'il suffit de construire en reportant au compas autour du cercle circonscrit la longueur de son premier arc DE en partant des points D, E et A déjà tracés (DE = EG = GH = HA = AI = IJ = JD).

Cette méthode permettant de tracer au moins un heptagone régulier de côté 1 (mais de rayon circonscrit au départ inconnu) permet ensuite de diviser un disque en 7 parties égales, en déplaçant le centre de cet heptagone de référence au centre du cercle à diviser, puis en utilisant la règle en s'appuyant sur le centre commun et les sommets du premier heptagone pour tracer les rayons coupant le cercle à découper en 7 arcs égaux :

Cette seconde construction ne nécessite que la règle et le compas pour faire « glisser » l'heptagone unitaire déjà construit pour faire coïncider les centres de l'heptagone déplacé avec le centre du cercle à diviser.

Il suffit juste de tracer une première droite joignant le centre du premier heptagone avec le centre du cercle à diviser, puis de tracer les parallèles passant par les sommets du premier heptagone, et de reporter au compas sur ces parallèles la distance entre les deux centres.

Une fois le second heptagone unitaire tracé et aligné au centre du cercle à diviser, il ne reste qu'à l'utiliser pour tracer les 7 rayons coupant le cercle à diviser et passant par les sommets de l'heptagone unitaire déplacé, pour obtenir un heptagone régulier de rayon quelconque inscrit dans le disque à diviser en 7 parts égales.

Constructions approchées[modifier | modifier le code]

À l'aide d'un triangle équilatéral[modifier | modifier le code]

Le rapport entre le côté de l'heptagone et le rayon du cercle circonscrit est de $2\sin(\pi /7)\approx 0{,}8677$ . Ce nombre est très voisin de ${\frac {\sqrt {3}}{2}}\approx 0{,}866$ et ce nombre est très facile à obtenir à l'aide d'un triangle équilatéral.

D'où la construction suivante :

Tracer un cercle de rayon 1 et de centre M.

Prendre un point X sur le cercle. Le cercle de centre X et de rayon XM rencontre le cercle précédent en A et Y

Les droites (AY) et (MX) se coupent en H.

La longueur AH est une bonne approximation du côté de l'heptagone inscrit dans ce même cercle.

Par cette méthode l'angle au centre est d'environ 51,32 degrés au lieu des 51,43 (environ) attendus, soit une erreur relative de 2,15 pour mille.

Heptagone régulier dans la vie courante[modifier | modifier le code]

La découpe de la pièce de 20 centimes d'euro est basée sur un heptagone régulier.
Les pièces britanniques de 20 et de 50 pence sont des heptagones de Reuleaux.

Fragments d'histoire[modifier | modifier le code]

L'heptagone est le premier polygone régulier à n'être pas constructible à la règle et au compas. Il est donc naturel qu'après la construction du pentagone et de l'hexagone, les Grecs puis les Arabes se soient penchés sur la construction de l'heptagone. Le seul texte d'origine grecque dont on ait trace sur une construction exacte de l'heptagone est attribué à Archimède : Sur la division d'un cercle en sept parties égales. Il nous est parvenu par une traduction arabe de Thābit ibn Qurra^[4]. La méthode de construction utilise une étape intermédiaire consistant à construire un point égalisant l'aire de deux triangles^[5] mais les détails de cette construction ne sont pas donnés. Les avis des commentateurs sont donc partagés : est-ce un trou dans la démonstration ? - la construction absente faisait-elle appel à une construction par neusis^[6] ? - le point a-t-il été obtenu par intersection de coniques ?

Nombreux sont les mathématiciens arabes à avoir commenté ce texte d'Archimède et dès le X^e siècle, des méthodes de construction utilisant l'intersection de deux coniques (deux hyperboles ou une hyperbole et une parabole) sont proposées, soit pour combler la lacune de la démonstration d'Archimède, soit pour proposer d'autres constructions (Abū al-Jūd, Al-Sijzi, Al-Saghani (en), Abū Sahl al-Qūhī, Ibn Sahl, Ibn al Haytham, Kamal al-Din ibn Yunus (mort vers 1242))^[7]. La relation existant entre la construction de l'heptagone et la résolution d'une équation de degré trois est étudiée dès Abu Nasr Mansur^[8].

De tous ces traités sur l'heptagone, il semble qu'aucun n'ait été traduit en latin. On trouve cependant trace d'une construction de l'heptagone faisant référence à la méthode d'Archimède dans le De Triangularis de Jordanus Nemorarius^[9].

Notes et références[modifier | modifier le code]

↑ Voir théorème 3.6, p. 195 de J.-M. Arnaudiès et P. Delezoide, « Nombres (2, 3)-constructibles », Adv. Math., vol. 158, n^o 2,‎ 2001, p. 169-252 (lire en ligne).
↑ Voir les p. 373-374 de J.-M. Arnaudiès et P. Delezoide, « Constructions géométriques par intersections de coniques », Bulletin de l'APMEP, vol. 446,‎ 2003, p. 367-382 (lire en ligne).
↑ Cette figure est abondamment détaillée dans le livre de Jean-Denis Eiden, Le jardin d'Eiden : Une année de colles en Math Spé MP, Paris, Calvage & Mounet, 2012, 690 p. (ISBN 978-2-916352-27-5).
↑ (en) Jan Hogendijk, « Greek and Arabic constructions of the regular heptagon », Arch. Hist. Exact Sci., vol. 30,‎ 1984, p. 197-330, p. 204.
↑ (en) Henry Mendell, « Archimedes and the Regular Heptagon, according to Thabit Ibn Qurra », sur CSULA.
↑ (en) Roshdi Rashed, Ibn Al-Haytham's Theory of Conics, Geometrical Constructions and Practical Geometry: A History of Arabic Sciences and Mathematics, vol. 3, p. 299 sur Google Livres.
↑ Hogendijk 1984, p. 201.
↑ Hogendijk 1984, p. 240.
↑ Hogendijk 1984, p. 270.

Voir aussi[modifier | modifier le code]

Sur les autres projets Wikimedia :

Heptagone, sur Wikimedia Commons
heptagone, sur le Wiktionnaire

Article connexe[modifier | modifier le code]

Formules trigonométriques en kπ/7

Liens externes[modifier | modifier le code]

Baptiste Gorin, À propos de l'heptagone régulier et de sa construction [PDF]
Autre construction approchée (GeoGebra avec règle et compas) . Précision : 0,1% .

Portail de la géométrie

[1] Voir théorème 3.6, p. 195 de J.-M. Arnaudiès et P. Delezoide, « Nombres (2, 3)-constructibles », Adv. Math., vol. 158, n^o 2,‎ 2001, p. 169-252 (lire en ligne).

[2] Voir les p. 373-374 de J.-M. Arnaudiès et P. Delezoide, « Constructions géométriques par intersections de coniques », Bulletin de l'APMEP, vol. 446,‎ 2003, p. 367-382 (lire en ligne).

[3] Cette figure est abondamment détaillée dans le livre de Jean-Denis Eiden, Le jardin d'Eiden : Une année de colles en Math Spé MP, Paris, Calvage & Mounet, 2012, 690 p. (ISBN 978-2-916352-27-5).

[4] (en) Jan Hogendijk, « Greek and Arabic constructions of the regular heptagon », Arch. Hist. Exact Sci., vol. 30,‎ 1984, p. 197-330, p. 204.

[5] (en) Henry Mendell, « Archimedes and the Regular Heptagon, according to Thabit Ibn Qurra », sur CSULA.

[6] (en) Roshdi Rashed, Ibn Al-Haytham's Theory of Conics, Geometrical Constructions and Practical Geometry: A History of Arabic Sciences and Mathematics, vol. 3, p. 299 sur Google Livres.

[7] Hogendijk 1984, p. 201.

[8] Hogendijk 1984, p. 240.

[9] Hogendijk 1984, p. 270.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]