Formule de Torricelli

Schéma de principe : un fluide s'écoule par une ouverture située à la distance $h$ du niveau de fluide.

Le principe de Torricelli est un principe de mécanique des fluides découvert par Evangelista Torricelli en 1643^[1]. Il établit que le carré de la vitesse d'écoulement d'un fluide sous l'effet de la pesanteur est proportionnel à la hauteur de fluide située au-dessus de l'ouverture par laquelle il s'échappe du cylindre qui le contient. Si on note $v$ la vitesse d'écoulement,

$h$ la hauteur de fluide et $g$ l'accélération de la pesanteur, on a^[1] :

v^{2}=2\,g\,h

Conséquences[modifier | modifier le code]

Une conséquence immédiate est que la vitesse est indépendante de la masse volumique du liquide considéré. Le mercure ou bien l'eau s'écoulent donc à la même vitesse. On retrouve ainsi la loi de Galilée sur la chute libre des corps transposée en hydrodynamique. Une autre conséquence de la formule de Torricelli est que plus la hauteur de liquide est importante, plus la vitesse d'éjection est élevée.

Énoncé historique[modifier | modifier le code]

En 1644, peu après la mort de Galilée (1564-1642), Torricelli (1608-1647) publie à Florence son de Motu aquarum^{[N 1]} dans lequel il énonce la loi dont il est aujourd'hui l'éponyme^[3]^,^[4]^,^[5]^,^[6]. Le philosophe et historien des sciences Michel Blay en résume ainsi l'énoncé^[3]^,^[4]^,^[5]^,^[6] : « la vitesse d'écoulement d'un liquide par le fond d'un réservoir percé est proportionnelle à la racine carrée de la hauteur séparant le trou de la surface libre du liquide. »

Un énoncé en a également été donné par Descartes en 1643 dans une lettre à Christian Huygens : « Les vitesses de sortie de l'eau par un trou placé en bas d'un cylindre sont en raison doublées des hauteurs de remplissage desdits cylindres^[7]. »

Démonstration[modifier | modifier le code]

La formule de Torricelli se démontre à l'aide du théorème de Bernoulli appliqué à une ligne de courant.

Le principe de conservation de l'énergie totale veut que la variation de l'énergie potentielle du fluide stocké se transforme en énergie cinétique du fluide qui s'écoule.

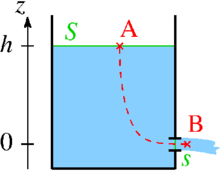
On considère une cuve remplie d'un liquide supposé parfait (non visqueux) et incompressible (masse volumique constante). Dans cette cuve est percé un trou de petite taille à une hauteur $h$ en dessous de la surface libre du liquide. On note $A$ un point choisi au hasard sur la surface libre du liquide et $B$ un point pris au niveau du jet libre généré par le trou.

On suppose que le trou est assez petit pour que :

le diamètre du trou soit négligeable devant la hauteur $h$ de liquide au-dessus du trou, de manière que $h$ puisse être considéré comme constant au niveau du trou ;
la surface $s$ du trou soit négligeable devant la surface libre $S$ du liquide ; la conservation du débit impose que $v_{\text{A}}S=v_{\text{B}}s$ , d'où $v_{\text{A}}={\frac {v_{\text{B}}\,s}{S}}\ll v_{\text{B}}$ ; on peut donc considérer que la hauteur $h$ ne varie pas au cours du temps, et que l'écoulement du liquide est permanent.

L'ensemble du liquide participant à l'écoulement, on peut relier les points $A$ et $B$ au travers d'une ligne de courant.

En admettant enfin que le champ de pesanteur est uniforme à l'échelle de la cuve, il est alors possible d'appliquer le théorème de Bernoulli au niveau des points $A$ et $B$ :

p_{\text{A}}+\rho \,g\,z_{\text{A}}+{\frac {\rho \,v_{\text{A}}^{2}}{2}}=p_{\text{B}}+\rho \,g\,z_{\text{B}}+{\frac {\rho \,v_{\text{B}}^{2}}{2}}\qquad [1]

Or la pression au niveau de la surface libre du liquide $p$ _A et la pression au niveau du jet libre $p$ _B sont toutes deux égales à la pression atmosphérique $p$ ₀. Par ailleurs on a vu que $v_{\text{A}}={\frac {v_{\text{B}}\,s}{S}}\ll v_{\text{B}}$ , donc on peut négliger la vitesse du liquide au point $A$ : $v_{\text{A}}=0$ . L'équation [1] devient alors :

p_{0}+\rho \,g\,z_{\text{A}}+0=p_{0}+\rho \,g\,z_{\text{B}}+{\frac {\rho \,v_{\text{B}}^{2}}{2}}

.

En simplifiant les pressions atmosphériques et la masse volumique, puis en isolant $v$ _B, on obtient la vitesse du liquide en sortie de la cuve :

v_{\text{B}}={\sqrt {2\,g\,(z_{\text{A}}-z_{\text{B}})}}={\sqrt {2\,g\,h}}

.

En considérant les différentes hypothèses nécessaires à l'établissement de cette formule, l'analogie avec la chute libre doit être interprétée avec précaution.

Remarque : la loi de Bernoulli n'avait pas encore été énoncée à l'époque où Torricelli propose cette loi. Cette démonstration n'est donc pas celle qui a pu le conduire au résultat.

Torricelli est-il l'auteur de la loi qui porte son nom ?[modifier | modifier le code]

Plus la hauteur de liquide est importante, plus la vitesse est grande.

Antérieurement à la publication des travaux de Torricelli, Mersenne a écrit de nombreuses lettres à Peiresc en 1634. En 1639, il semble que Descartes le félicite pour sa loi qui calque « par anticipation » celle de Torricelli. Ces écrits sont conservés aux Arts et Métiers à Paris.

Descartes, Mersenne, Gassendi écrivent beaucoup jusqu'en 1643 et après. Les difficultés sont bien cernées : niveau d'eau constant, perte de charge en cas de rétrécissement, problème de la buse de sortie, et bien évidemment le jet d'eau et la loi de 1638 de Galilée (4^e journée). Hydraulica de Mersenne paraît en 1644 et Mersenne rencontre Torricelli en 1645. Si les vases communicants font remonter l'eau au niveau du lac, il est manifeste que le jet d'eau dirigé verticalement n'y remonte pas vraiment, et chacun voit bien ce que produit la modification de la buse dans un jet d'arrosage. La démonstration dépasse manifestement les physiciens de l'époque.

Postérieurement, en 1668, à l'Académie des Sciences de Paris, Christian Huygens et Jean Picard, puis Edme Mariotte reprennent le problème.

En 1695, donc après Leibniz (1684), Pierre Varignon raisonne ainsi :

« La petite masse d'eau

ρ S d x

est éjectée par la force de pression

S ρ g h

avec une quantité de mouvement

ρ S d x v

pendant le temps

d t

: soit

v 2 = g h

»

mais il y manque toujours le facteur 2.

Cela dit, à l'époque la force vive se calculait $m v 2$ ; elle a été renommée énergie cinétique et a pris la valeur $1 / 2 m v 2$ pour que sa dérivée soit ${\frac {\mathrm {d} E_{c}}{\mathrm {d} t}}=m\,{\vec {v}}\cdot {\frac {\mathrm {d} {\vec {v}}}{\mathrm {d} t}}={\vec {p}}\cdot {\vec {a}}={\vec {F}}\cdot {\vec {v}}$ à la suite des travaux de Gaspard-Gustave Coriolis et Jean-Victor Poncelet sur la période 1819-1839.

En 1738, Daniel Bernoulli donne enfin la solution dans son Hydrodynamica.

Notes et références[modifier | modifier le code]

Notes[modifier | modifier le code]

↑ Le de Motu aquarum de Torricelli appartient au livre II de son de Motu gravium naturaliter descendentium et projectorum, celui-ci étant le deuxième des trois traités de ses Opera geometrica^[2].

Références[modifier | modifier le code]

↑ ^{a et b} Torricelli’s theorem. Encyclopædia Britannica. Encyclopædia Britannica Online. Encyclopædia Britannica, 2011. Consulté le 30 janvier 2011. Lire en ligne.
↑ Blay 1987, p. 79, n. 1.
↑ ^{a et b} Blay 1985, p. 330.
↑ ^{a et b} Blay 1987, p. 79.
↑ ^{a et b} Blay 1992, p. 51.
↑ ^{a et b} Blay 2005.
↑ Vincent Jullien et André Charrak, Ce que dit Descartes touchant la chute des graves: 1618 à 1646, étude d'un indicateur de la philosophie naturelle cartésienne, Presses Univ. Septentrion, coll. « Histoire des sciences », 2002, 214 p. (ISBN 2859397523 et 9782859397524), p. 193

Voir aussi[modifier | modifier le code]

Bibliographie[modifier | modifier le code]

: document utilisé comme source pour la rédaction de cet article.

[Blay 1985] Michel Blay, « Varignon et le statut de la loi de Torricelli », Archives internationales d'histoire des sciences, vol. 35, n^os 114-115,‎ 1985, p. 330-345 (OCLC 5894334736).
[Blay 1987] Michel Blay, « La loi d'écoulement de Torricelli et sa réception au XVII^e siècle », dans François de Gandt, L'œuvre de Torricelli : science galiléenne et nouvelle géométrie, Nice, Université de Nice, faculté des lettres et sciences humaines (diffusion Les Belles Lettres), coll. « Publications de la faculté des lettres et sciences humaines de Nice / 1^re série » (n^o 32), 1987 (réimpr. 1989), 1^re éd., 247 p., ill. et fig., 22 cm, broché (ISBN 2-252-62032-X (édité erroné) et 2-251-62032-X, OCLC 19995570, BNF 35010175, SUDOC 001438921), p. 79-110.
[Blay 1992] Michel Blay, « Deux exemples de l'influence de l'école galiléenne sur les premiers travaux de l'Académie royale des sciences de Paris », dans Massimo Bucciantini et Maurizio Torrini (éd.), Geometria e atomismo nella scuola galileiana (acte du colloque tenu à Paris du 24 au 26 oct. 1988), Florence, L. S. Olschki, coll. « Biblioteca di « Nuncius » / Studi e testi » (n^o 10), 1992, 1^re éd., VII-213 p., fig., 17 × 24 cm, broché (ISBN 88-222-4008-1, EAN 9788822240088, OCLC 463614668, BNF 35552806, SUDOC 012498661, présentation en ligne), p. 49-65.
[Blay 2005] Michel Blay, « Les débuts de la science du mouvement des eaux », Les Génies de la science, n^o 22 : « La science au temps des mousquetaires »,‎ février-mai 2005, p. 110-119 (lire en ligne ).
Antonio Nardi, « Théorème de Torricelli ou théorème de Mersenne », Les Études philosophiques, n^os 1-2 « Études sur Marin Mersenne »,‎ janvier-juin 1994, p. 87-118 (JSTOR 20848825).
(la) Evangelista Torricelli, Opera geometrica (faux-titre), Florence, A. Massi et L. Landi, 1644, 1^re éd., [1]-243 et [1]-151, fig. et tabl., in-4^o (OCLC 488408320, BNF 31482171, lire en ligne ).