Discussion:Sudoku
- Admissibilité
- Neutralité
- Droit d'auteur
- Article de qualité
- Bon article
- Lumière sur
- À faire
- Archives
- Commons
Archives[modifier le code]
X-Wing et Swordfish ?[modifier le code]
C'est où ? C'est quoi ? IP enregistrée 20:05, 1 Mars 2006 (UTC)
Liens externes[modifier le code]
Je tente une solution, je vais me faire taper sur les doigts pour abus de pouvoir, déstabilisation de l'organisation interne du Wikid.. je le sais... J'ai fait une sous-page Sudoku/Liens_externes et je l'ai bloquée pour limiter ces ajouts énervants de liens externes tous plus inutiles les uns que les autres. Dake* 25 décembre 2005 à 20:46 (CET)
- C'est surtout en attendant que le système des pages "semi-bloquées" soit activé (pas de contributions sous IP, seulement les utilisateurs enregistrés depuis plus de 4 jours). Dake* 25 décembre 2005 à 21:04 (CET)
- ne faudrait-il pas ajouter le bandeau Page protégée sur Sudoku/Liens externes ? Florent 4 janvier 2006 à 14:19 (CET)
- je l'ai déprotégée, mon but était surtout d'isoler tous ces reverts d'IP de l'article principal qui est un AdQ. J'attends toujours l'arrivée de la semi-protection :) Dake* 4 janvier 2006 à 14:33 (CET)
- ne faudrait-il pas ajouter le bandeau Page protégée sur Sudoku/Liens externes ? Florent 4 janvier 2006 à 14:19 (CET)
Semi-protection activée Dake* 24 janvier 2006 à 09:40 (CET)
- \o/ DarkoNeko (漫画) 24 janvier 2006 à 09:42 (CET)
- y'en avait franchement marre de ces URL à 2.- Dake* 24 janvier 2006 à 09:58 (CET)
- je suis d'accord avec la semi-protection. ~Pyb 24 janvier 2006 à 11:11 (CET)
- y'en avait franchement marre de ces URL à 2.- Dake* 24 janvier 2006 à 09:58 (CET)
S'il vous plaît remplacez le lien externe Samurai Su Doku de http://sudoku.top-notch.co.uk/gattai5.asp (commercial) avec http://www.samurai-sudoku.com/ (non-commercial, solveur). Kristinw 28 février 2006 à 12:15 (CET)
De même, en bon français, dans la section source:
- (en) Indices pour solutionner au site Puzzle Japan
doit être changé en:
- (en) Indices pour résolution sur le site Puzzle Japan
pour le lien: http://www.puzzle.jp/keys/sudoku_keys-e.html . Fabien [dim jun 25 22:24:52 CEST 2006]
- Je ne suis pas d'accord à un ajout sur l'article : le premier est lien mort et le second est un forum avec attention 14 messages et 6 membres...
- Eric 20 mars 2007 à 19:49 (CET)
- ok! c'est comme vous voulez! Je viens d'effacer mes ajouts... Farid
Le problème des 36 officiers de Euler[modifier le code]
Je ne vois pas pourquoi on met sans cesse en avant le problème des 36 officiers de Euler dans tous les articles sur le Sudoku, alors qu'il s'agit d'un carré greco-latin et non pas latin, qui est certes intéressant, mais beaucoup plus en rapport avec les recherches sur l'existence des carrés greco-latins. Le Sudoku est un carré latin avec 9 sous blocs qui resteignent les possibilités et permettent la résolution unique.
- Sûrement pour dissiper la confusion qui règne autour de l'invention du Sudoku. Cela montre qu'Euler s'est intéressé à un problème apparenté (une grille avec des contraintes), sans toutefois avoir inventé le Sudoku. Certains semblent attribuer la paternité du Sudoku à Euler [1]. Dake* 24 janvier 2006 à 19:35 (CET)
Sur le site proposé en lien, comme sur d'autres sites reliant Euler et le Sudoku, le point avancé est que Euler s'est intéressé aux carrés latins, ce qui est vrai (inventé est peut-être un peu fort mais disons qu'il les a mis à la lumière.). Ils en arrivent parfois un peu trop vite à la conclusion qu'il a inventé le Sudoku, or l'ajout capital des Sudoku est les sous-zones qui restreignent les possibilités. On peut donc noter qu'il n'a pas fait cet ajout décisif pour créer le jeu Sudoku. Mais le problème des officiers n'a rien à voir avec cet histoire (structure très différente), à part le fait qu'il peut également être assimilé à un jeu.
- pas tout à fait d'accord avec l'absence totale de lien entre les 36 officiers et le Sudoku. Le carré gréco-latin empêche la répétition de la même paire, tout comme la règle concernant les chiffres dans une sous-région du Sudoku. Je crois que cette contrainte est intéressante car elle n'existe pas dans le carré latin, mais existe dans le Sudoku. En gros, les 36 officiers sont à mi-chemin entre le carré latin (si on regarde la grille du Sudoku dans son ensemble lignes/colonnes), et le Sudoku (carré latin + contraintes régionales de type carré gréco-latin). Mais il est clair que faire le raccourci "Euler a inventé le Sudoku" est une erreur. Dake* 26 janvier 2006 à 22:15 (CET)
Ajout d'un lien externe[modifier le code]
http://www.daily-sudoku-puzzle.com/fr Est-il possible de proposer ce site dans l'article du wikipédia ?
Il présente les règles du jeu grâce à une vidéo http://www.daily-sudoku-puzzle.com/regles-sudoku.html
Des grilles sont jouables en ligne avec possibilité de jouer en couleurs, avec un système d'annotation comme aide à la résolution
Ce site propose des grilles de plusieurs niveaux (facile, moyen, difficile et diabolique): 4 nouvelles grilles chaque jour. Elles sont imprimables.
Les internautes ont la possibilité de proposer leur grille (Grille Perso) pour la présenter aux autres.
Et aussi un générateur de grilles selon les 4 niveaux
Interessant : Les internautes peuvent communiquer et commenter chaque grille Ce système s'avère très instructif car les internautes suggèrent des idées, et mettent en évidence l'utilisation de techniques pour joueurs confirmés (les dialogues sont particulièrement soutenus dans le mode diabolique qui nécessite souvent une réflexion plus intense)
ex: http://www.daily-sudoku-puzzle.com/fr/sudoku-perso21.html
Cordialement Nicolas
- Ok, je vais mettre un lien vers l'animation en particulier, cela peut être intéressant. Dake* 24 janvier 2006 à 23:40 (CET)
http://fr.wikipedia.org/wiki/Discuter:Sudoku#Ajout_d.27un_lien_externe
Ajout d'un lien externe[modifier le code]
Est-il possible de proposer ce site dans les liens externes (rubrique Logiciels) :
http://d.ch.free.fr/sudoku.html
Ce site présente un logiciel gratuit (permettant de résoudre n'importe quelle grille, et soumet des grilles à résoudre par le joueur) , il est illustré d'astuces pour résoudre les grilles. Salutation amicales Dominique
'Le Sudoku (prononcer [sudoku])'[modifier le code]
Je ne connais pas la prononciation exacte, ce n'est donc pas une question de fond, mais de forme.
A quoi sert de préciser qu'il faut prononcer 'sudoku' le mot 'sudoku' ?
- Il s'agit de la transcription en alphabet phonétique international. En "français", ça se prononce "sou do kou". Guffman 22 mars 2006 à 00:13 (CET)
- Merci de ta réponse
- Je me suis toutefois permis de mettre les deux sur l'article, je pense que je ne suis pas qqun d'exceptionel, si j'ai tilté, d'autres se demanderont quoi aussi. Eric
- Tu as bien fait. Dake@ 22 mars 2006 à 14:06 (CET)
- Je ne suis pas d'accord : en français, ça se prononce /sudoku/. « sou do kou » n'est pas une transcription phonétique. R 29 mars 2006 à 08:20 (CEST)
- Bon ben j'abdique, j'ai d'autres soucis et d'autres priorités qu'entretenir un débat sur une histoire de codifications. MAIS je maintiens et je signe que cette notation est très ambigüe pour un non initié, et même si il avait la présence d'esprit de cliquer sur le lien Alphabet Phonétique International (0,01% des utilisateurs), de le lire (0,001% des utilisateurs), de le comprendre alors que ce n'était pas la raison de sa visite (0,0001% des utilisateurs), je ne suis pas sur qu'il le prononce correctement ce mot.
- Pour moi, trop de rigidité fait perdre en qualité de l'article
- Ce n'est que mon avis.
- et je le partage HB 29 mars 2006 à 19:15 (CEST)
- Je ne suis pas d'accord : en français, ça se prononce /sudoku/. « sou do kou » n'est pas une transcription phonétique. R 29 mars 2006 à 08:20 (CEST)
- Tu as bien fait. Dake@ 22 mars 2006 à 14:06 (CET)
- La graphie en français étant "sudoku" et non pas "soudokou" (je ne sache pas que le japonais recoure à l'alphabet latin !), il convient donc de prononcer la voyelle "u" comme on le fait en français. On ne dit pas "joudoka", on n'écrit pas "samurai" non ? Un peu de cohérence ne nuit point.
ajout essais temporaire[modifier le code]

Le Sudoku (Japonais: 数独, sūdoku), est un jeu de logique composé d'une grille de 9 lignes et 9 rangées, subdivisée en 9 régions de 9 cases chacunes. Le but du jeu est de placer chaque chiffre de 1 à 9 dans chacune des rangées, colonnes et régions sans qu'un nombre donné apparaisse plus d'une fois dans une rangée, colonne et région. Une grille nouvelle débute avec quelques chiffres déjà en place et le joueur doit, par déduction logique, placer les chiffres manquants dans chacune des cases vierges.
Introduction[modifier le code]
Le terme Sodoku est l'abréviation de la phrase japonaise "suuji wa dokushin ni kagiru (数字は独身に限る)," qui se traduit par "chaque chiffre reste seul". C'est une marque de commerce de l'éditeur de jeux japonais Nikoli. Les autres éditeurs japonais appellent ce jeu "le nombre à sa place" et son titre original aux États-Unis où origine en fait ce jeu est Number Place.
Notons que l'utilisation de chiffres est tout à fait faculatative. Il n'y a absolument aucune relation mathématique entre les différents symboles utilisés pour ce jeu. Il existe des variantes utilisant des lettres, des couleurs ou des formes géométriques. L'utilisation de chiffres remonte cependant à la création d'un jeu en 1979.
L'intérêt principal de ce jeu repose sur la simplicité de ses règles mais également que le jeu peut être en soi très complexe à réaliser. Il existe plusieurs niveaux de difficultés, allant de débutant à très avancé.
- Bon, ça c'est de moi. J'avais débuté un article sous Sodoku (jeu) quand quelqu'un m'a rappellé à l'ordre. J'ai tout viré (dans Sodoku (jeu)]] pour remplacer tout ça par un REDIRECT. Par contre, je persiste et signe, l'orthographe Sodoku existe également . Yanik Crépeau 29 mars 2006 à 07:50 (CEST)
origine? article illogique[modifier le code]
l'article est pas logique: c'est un americain qui invente le sudoku,et a la fin du paragraphe, on explique que les japonais l'ont inventé a cause du manque de mot croissé (ce qui est faux, en plus, les mtozs crosié existe en japonais, ils ont des sillabaires, donc c'est possible...). dont QUI l'a inventé ? si c'est americain, il faut retirer le passage "les japonais blabla"
- La tournure était mauvaise, j'ai corrigé pour signifier que les Japonais ont apprécié et répandu le concept pour les raisons indiquées. C'est bel et bien un Américain qui a inventé le jeu. Dake@ 30 mars 2006 à 13:33 (CEST)
des origines françaises[modifier le code]
le texte est protégé je ne sais donc pas comment ajouter... voici une dépeche qui résume ce que je voulais synthétiser : Le sudoku a des ancêtres français
PARIS (AP) - Le sudoku n'est apparemment pas une invention récente comme beaucoup le pensaient. A la fin du XIXe siècle, les Français jouaient en effet à remplir des grilles très proches de ce jeu, qui étaient publiées dans les grands quotidiens de l'époque, révèle "Pour la Science" dans son édition de juin.
Selon le magazine, la grille la plus proche d'un sudoku, qui a été retrouvée par le Français Christian Boyer, est celle de B. Meyniel, publiée dans le quotidien "La France" du 6 juillet 1895. Les premiers sudokus ont été publiés en 1979 par l'Américain Howard Garns, avant de paraître dans des revues japonaises des années 80 et 90 où ils ont pris leur nom. Mais leur succès international a vraiment démarré grâce au Néo-Zélandais Wayne Gould qui en a publiés dans le "Times" de Londres à partir de novembre 2004. AP
- article du même type dans le quotidien Le Parisien du lundi 5 juin 2006 (page 7). L'article est titré "l'inventeur du sudoku est français". Il fait référence à un article paru dans la revue "Scientic American". Les premières grilles de type sudoku datent de 1892 et furent publiées dans le journal "Le Siècle". La première "vraie" grille grille de sudoku date bien du 6 juillet 1895 ; elle fut publiée par le journal "La France". L'article précise également que "l'engougouement des Français pour ces passe-temps avait duré jusqu'à la Première Guerre mondiale". Clio64 5 juin 2006 à 20:49 (CEST) PS : l'article de la Wikipédia anglophone est d'ailleurs bien plus précis que celui de l'édition francophone à ce niveau... Un petite traduction, au minimum, s'impose... Clio64 5 juin 2006 à 20:54 (CEST) PS2 : article du quotidien The Times (3 juin 2006) qui reprend également ces données [2]. Clio64 5 juin 2006 à 21:03 (CEST)
Ajout d'un lien externe[modifier le code]
Est-il possible de ajouter un lien au site http://www.sokudo.be/sudoku/ dans l'article?
Il offre plusieurs grilles en quatre niveaux avec des options qui aident à trouver la solution et qui peuvent donc aider les nouveaux joueurs.
d'apres mes amis japonais (10 differents): 1) le sudoku est vraiment peu connu au japon. 2) les mots croisé sont vraiment 10000 fois plus populaires. merci de retiré le truc sur "les japonais blabla alphabets". ils ont un sillabaire qui leur permet tres bien d'y jouer.
Ajout d'un lien externe[modifier le code]
Bonjour !
J'ai créé un site qui effectue des tests comparatifs de revues de sudoku, annonce des tournois, et offre plusieurs autres infos en relation avec le sudoku. Son adresse est la suivante : http://www.sudokuinfo.net
Je propose de le mentionner dans la contribution consacrée au sudoku, car j'ai l'espoir qu'il puisse renseigner utilement pas mal de personnes ;)
Je précise qu'il ne contient pas de pub et que je n'en tire aucun revenu.
Steve
ben non ca va pas être possible cordialement
Besoin d'un éditeur pour la partie Math[modifier le code]
Bonjour aux amateurs,
Il y a une requète d'édition sur Wikipédia:Demande_d'intervention_sur_une_page_protégée#Sudoku (Attention, il y a 2 sections, l'une en dessou de l'autre. Il s'agit de la seconde). Si l'un d'entre vous pouvait y jeter un oeil et appliquer, si justifiées, les modifications demandées, puis le signaler sur la page sus-mentionnée, ça serait sympa! Merci d'avance Eden ✍ 14 avril 2006 à 23:08 (CEST)
Bonjour de modification[modifier le code]
Je me repete mais il faut retirer la phrases "les japonais jouent beaucoup au sudoku car leur alphabet leur permet pas de faire des mots croisé". Le Sudoku est quasi inconnu au japon, et les mots croisés tres populaires. Leur sylabaire de 55 lettres leur permet facilement d'en faire. on parle du japon, pas de la chine.
- Non. Pour l'instant, rien ne confirme l'absence de popularité au Japon, il faut donner des sources, car partout je lis que le Sudoku est populaire dans ce pays. De plus, un grand nombre de résultats mathématiques sur ce jeu viennent du Japon. Dake@ 17 avril 2006 à 16:31 (CEST)
Tu le lis peut etre mais apres 25 demandes a des japonais: c'est quasi inconnu. les mots croisées sont tres populaires. source: tout mes amis , ma copine. tu veux ptet leur msn???
- C'est vrai que la copine, c'est vraiment l'argument qui tue :D
Enfin bref, à part cette remarque j'en sais rien, mais on trouve mieux comme source ;) Van Kanzaki (話す) 25 avril 2006 à 12:53 (CEST)
ma copine, plus de 10 japonais, il te faut une petition ou quoi? demande a nicolas, ton cher president, qui parle courrament japonais .... SInon,enquete par toi meme...(au passage, van c'est plus hollodais que japonais hihi). Je suis heureux qu'a wikipedia, encyclopedie "libre" il faut PROUVER ce que l'on dit.Mais par contre, on peut repeté n'importe quoi. Sudoku est VRAIMENT inconnu au japon. je peux VRAIMENT te donner 10 msn de personne qui vivent au japon et qui ont jamais entendu parler de ca. LEs mots croisés sont tres populaire, et dans tout les journaux japonais. tu peux en acheter a paris. Tu as quoi comme source japonaise pour affirmer que les mot croisé existe pas? je te rappel que l'alphabet japonais peu faire des mot croisé. ne confond pas avec le chinois.il y a un tres bon portail sur le japon, ici. c'est enervant de vouloir essayé d'aider les gens. (au passage Van machin est passionné de japon,mais pas japonais...) Ma copine: pourquoi c'est connu que les japonais jouent au sudoku???(marketing je pense)
- Bon, alors d'abord il me semble important de ne pas s'énerver, hein. Parce que c'est l'impression que ça donne, ici. Ensuite, je me moque que Van soit hollandais, japonais, ou quoi que ce soit d'autre, c'est juste un pseudo. Enfin, je signalais juste que l'expression "ma copine m'a dit..." est assez ridicule, de même que dans une copie d'examen, dissertation par exemple, on ne cite pas son prof et encore moins Yoda. Et sinon, je n'ai pas compris la remarque sur ma nationalité. Mais passons...
- En gros, il ne suffit pas de "msn" ou de "copine" pour affirmer quelque chose. Ce qu'on pourrait trouver un peu plus probant, ce serait par exemple un article de journal, un site sérieux, etc. Mais après tout, ce que j'en dis... Van Kanzaki (話す) 27 avril 2006 à 00:19 (CEST)
comme j'ai dit je peux PROUVER ce que je dis.et toi,ou sont tes sources? trouve UN journal japonais sans mot croisé et avec un sudoku. enfin meme,trouve un journal japonais avec un sudoku. moi,mes 10 amis du japon,ma copine du japon,tout ces amis ne me permettent pas de dire que les japonais sont fans du sudoku (dont ils ne connaissent pas le nom!). toi,comment prouves tu que c'est tres populaire au japon? SOURCE? SOURCE? (du japon,pas des ont dit).Source.
Le bilboquet est finlandais,c'est un grec qui m'a dit qu'il me la dit.il la vu a la tele.
merci,je passe mon temps a corriger un article qiu ets sois disant de qualité.4eme fois.
c'est ca la qualité wikipedia?cité un grec pour justifié un article finlandais? (regarde la distance grece finlande et japon vietnam).c'est ca tes sources?
bon mon pote josé me dit que le sudoku est portuguais,vas-y,modifit.
- J'ai demandé sur la Wikipédia japonaise et la première réponse semble aller en ce sens : http://ja.wikipedia.org/wiki/Wikipedia:Chatsubo_for_Non-Japanese_Speakers#Sudoku -- Dake@ 21 mai 2006 à 16:21 (CEST)
- Pour amener de l'eau au moulin, je rentre tout juste du Japon. Il est vrai que le Soduku était peu connu il y a encore quelques mois mais il commence à se developper maintenant sous le nom "Number place". --Kariboo37 4 novembre 2006 à 18:18 (CET)
logiciel generant des sudoku, pour jouer sur son ordi ou à imprimer[modifier le code]
Existe t il de tels logiciels ? Si oui y a t il un article/liste là dessus sur wikipédia ? Si oui il faudrait mettre un lien sur cette page.
- Régulièrement un nettoyage de cet article est effectué, car les créateurs de logiciels profitent de la visibilité de Wikipédia pour faire de la pub sans équivoque "SuperSudoku, le meilleur logiciel, cliquez ici !"
- Bilan, comme on peut difficiliement ce positionner en tant que juge, on a tendance à tout supprimer.
- Par ailleurs, ce type de logiciel, très fréquent, est facilement obtenable sur des sites comme Telecharger.com
- Eric 19 mai 2006 à 21:49 (CEST)
- Oui, on ne vient pas sur wikipedia pour jouer au sudoku (ou trouver des liens), mais pour savoir ce dont il s'agit. --Meithal 21 mai 2006 à 01:11 (CEST)
Merci...Oui apres avoir demandé a plus de 50 japonais, c'est vraiment beaucoup plus connu/joué en france. Et les mots croisés sont tres populaires au japon...le "probleme de leur alphabet" n'a jamais existé. Donc, modification? plus d'un mois que j'attends...
- Notre devise, c'est "juste fais-le". Dake@
- Page semi protégé, et a chaque changement, l'auteur annule les modifs :( Fabi__ 26 mai 2006 à 18:13 (CEST)
Proposition pour des explications plus détaillées sur les diverses méthodes de résolution[modifier le code]
En tant que lecteur régulier de fr.wikipédia, j'ai naturellement consulté l'article Sudoku quand, après quelques essais de grilles proposées dans divers journaux ou revues, je me suis rendu compte qu'il fallait que j'améliore grandement mon niveau de capacité de résolution en creusant la question des bases théoriques de résolution. Or, si l'article m'a paru globalement très intéressant (notamment parce qu'il aborde le sujet sous des angles très variés - à ce titre il mérite sans conteste sa mention "article de qualité"), le chapitre 7 (méthode de résolution) m'a laissé sur ma faim car il est à la fois assez peu explicite et surtout fort lacunaire (car bien des méthodes "classiques" ne sont pas évoquées).
Or, ayant déjà rédigé une douzaine d'articles (sur des sujets variés) pour wikipedia et ayant une certaine expérience de l'enseignement (~20 ans), je me suis donc attelé à la tâche et, après avoir consulté tous les articles disponibles sur le web (en anglais ou en français), j'ai confectionné une page html largement illustrée d'exemples et qui, répondant à ce que j'aurais aimé trouver dans l'article, fait le point sur toutes les méthodes classiques (exception faite pour le "nishio" et autres méthodes "au petit bonheur", car sur ce point je fais partie des puristes) !
Comme je ne veux pas indisposer Dake auquel je tiens au contraire à rendre hommage, je voudrais lui faire parvenir par mail cette page pour qu'il décide lui-même s'il convient ou non, d'en utiliser le contenu dans wikipédia, et si oui, sous quelle forme :
- complément au chapitre 7
- ou remplacement du chapitre 7 par un simple lien interne vers un nouvel article qui pourrait s'intituler "Sudoku - Méthodes de résolution" (le s du pluriel me paraît préférable)
.
Mais comment faire pour rendre possible ce mail destiné à Dake ?
Dake, si tu es intéressé par ma proposition, peux-tu (sans que cela t'engage pour la suite à donner) prendre contact avec un administrateur pour que celui-ci nous donne les moyens d'entrer en contact (je suis prêt à te donner mon adresse e-mail, mon téléphone ou mon adresse postale ..., mais bien sûr pas ici !)
Salut ! Papy77 20 juin 2006 à 18:57 (CEST)
Rédaction finalisée de l'article[modifier le code]
Je crois que l'article devient de plus en plus incohérent au niveau de la rédaction, du fait des ajouts continuels des contributeurs, chacun de l'angle dont il voit les choses.. Moi même j'ai pu insérer quelques paragraphes ( construction des grilles, degré de difficulté, et méthode de résolution), mais je crois qu'il faut que quelqu'un prenne en charge la rédaction finalisée de tout l'article et opte pour le choix d'une seule terminologie pour l'heuristique de résolution par exemple.. Je ne me propose pas pour réussir cette tâche mais je reste à la disposition pour concertation surtout au niveau de la mise à jour des sous-paragraphes en ce qui concerne les procédés de résolution,...--Farid MITA 22 mars 2007 à 16:49 (CET)
Fubuki et Kakuro[modifier le code]
Dans les DNA (dernières nouvelles d'Alsace) du jour un article non accessible gratuitement. Fafnir 30 juillet 2006 à 08:44 (CEST)
Version plus améliorée de Su-Doku: Su-Doku-Tartib [modifier le code]
Le jeu de Su-Doku-Tartib est une version plus évoluée du Su-Doku classique qui consiste à respecter, en plus de la règle habituelle « Chaque chiffre de 1 à 9 est écrit une et une seule fois dans chaque région, chaque ligne et chaque colonne », l'ordre imposée par les signes < (chiffre de gauche inférieur à celui de la droite), > ( chiffre de gauche supérieur à celui de la droite), v ( chiffre du haut supérieur à celui qui est placé dans la case du bas) et ^ ( chiffre de la case du bas supérieur à celui de la case du haut).
Jouer au Su-Doku-Tartib 9X9, c’est compléter une telle grille dont certains chiffres sont connus en découvrant les cachés par des déductions successives ou par des éliminations régies par la contrainte des régions, des lignes et des colonnes tout en respectant l'ordre indiqué par les différents symboles <, >, ^ et v.
Bien sûr, une stratégie de résolution existe, procurant plus de plaisir à celui qui s'y adonne. En plus des trois procédés habituellement utilisés pour la réussite du Su-Doku classique, on pourra d'abord inscrire les chiffres 1 et 9 dans les cases facilement repérables par les signes d'ordre, puis voir les possibilités pour les deux chiffres 2 et 8, etc... Les mêmes signes d'ordre serviront à simplifier les multiples dans des cases adjacentes...
--Farid MITA 22 mars 2007 à 17:32 (CET)
Fédération Française de Sudoku[modifier le code]
J'ai rajouté un lien vers le site de la Fédération Française de Sudoku... (www.ffsudoku.com) était-ce une bonne idée ? On garde ou on jette ? ^_^" Merwyn 7 août 2006 à 19:45 (CEST)
Résolution sous excel[modifier le code]
J'ai fait un petit programme de résolution sous Excel. Si ça vous interresse pour illustrer vos dires... Il n'est pas superbement pofiné (comme votre article) mais il tourne! résolution en 2 secondes!
--Gerbito 25 août 2006 à 14:35 (CEST)
Swordfish[modifier le code]
Je viens de lire cette discussion et me demande si j'ai bien fait.
J'ai lu avec intérêt cet article et y ai trouvé un lien rouge. Mais comment, un article lu par des milliers de wikipédien, top du top, qui a un lien rouge ! Personne n'a écrit l'article sur le swordfish ?
Alors j'ai décidé de me lancer dans la rédaction d'une première page et essayé d'expliquer ce qu'est un Swordfish !
J'espère que je ne vais pas me faire lyncher, au vu de certains des échanges un peu chauds sur cette page.
Je suis quand même un peu surpris que Swordfish renvoie sur la page Opération Espadon. Si quelqu’un veux vérifier si c’est bien correct par rapport aux règles wikipédiennes.
Bien à vous
Philoo 15 mars 2007 à 20:10 (CET)
Résolution[modifier le code]
Je signale que, comme annoncé ici le 20 juin 2006, je me suis enfin décidé à écrire un article consacré entièrement aux techniques de Résolution d'un sudoku.
Les amateurs pourront peut-être se consacrer à la re-rédaction (ou à l'élimination) d'articles conjoints ... (bon courage !)
91.168.56.194 2 juin 2007 à 08:27 (CEST)
Importance de l'article[modifier le code]
Je conteste la classement en importance "maximum" de l'article, je change pour le "élevé"(ça ne le mérite même pas finalement...) "moyenne" si vous êtes pas d'accord vous pouvez toujours l'y replacer en argumentant (un minimum) ci-dessous. Pour ma part le Sudoku ne correspond pas a un "sujet est très important au niveau universel [...]". Cordialement, Raziel {boudoir} 7 juin 2007 à 21:35 (CEST)
- Donc, depuis longtemps, l'article est sans importance! Ces derniers jours, seuls deux utilisateurs et moi nous y intéressons! Sans parler des administrateurs qui s'occupent du côté technique et de la régulation...--Wikasterix (d) 22 mai 2009 à 18:08 (CEST)
- En revenant à la version de Farid Mita, vous supprimez en particulier des modifications beaucoup plus intéressantes d'un autre contributeur.
- Je n'ai ni le temps ni le désir de refaire ce que vous passez votre temps à défaire. Si c'est comme ça que marche wikipedia, alors ce sera sans moi.
- Cordialement — Le message qui précède, non signé, a été déposé par l'IP 92.140.82.217 (discuter)
- Je vous demandais simplement de motiver votre modification en page de discussion j'y copie colle ceci. Micthev (Discuter) 25 avril 2009 à 02:12 (CEST)
- voir [3] et [4] a priori c'est sérieux ATTENTION j'ai pas tout lu non plus mais si les modifications sont lourdes ... il faut les motiver --Neuromancien (@+2P) 25 avril 2009 à 05:34 (CEST)
- Bonsoir je ne remets pas en cause votre savoir et la pertinence de vos remarques mais il faut voir avec l'intéressé Farid mita, qui n'est pas un total inconnu ( ce qui du coup me fait relativiser votre science ) il est l'auteur du manuel "Stratégie de résolution d'une grille de Sudoku (le lien est cassé hélàs, lycos.fr semble-t-il n'existe plus ).Je vous suggère d'en discuter avec lui pour élaborer ensemble une page meilleure que j'aurai le plaisir de lire bientôt. Je vous suggère aussi d'éviter les mises en cause personnelles et la lecture de Wikipédia:Supposer la bonne foi--Neuromancien (@+2P) 25 avril 2009 à 05:48 (CEST)
- Je vous demandais simplement de motiver votre modification en page de discussion j'y copie colle ceci. Micthev (Discuter) 25 avril 2009 à 02:12 (CEST)
Réponse : J'avais évidemment vu cette référence, qui n'a aucun ISBN et n'a jamais été commentée nulle part. Farid MIta est donc bien un total inconnu dans le monde du sudoku : il ne participe à aucun forum sur le sudoku, Le caractère évident d'auto-propagande de ces ajouts n'aurait pas dû vous échapper.— Le message qui précède, non signé, a été déposé par l'IP 92.140.82.217 (discuter)
- J'ai signalé le problème à cet utilisateur je vous suggère juste d'attendre un peu avant de procéder à une refonte. La page de discussion est là pour discuter de çà. Evitez les mises en cause personnelles. Pour faciliter les débats et éviter d'encombrer la page d'une IP potentiellement dynamique vous pouvez aussi créer un compte celà vous permettra de faire des modifications plus facilement et d'être vous même moins remis en cause que lors d'éditions anonymes toujours sujettes à vérification.Ensuite soyez rassuré l'historique de la page permettra de récupérer vos contributions le cas échéant. Personnellement je ne suis pas un spécialiste de la question donc je ne me prononcerai pas sur la pertinence des modifications. Cordialement --Neuromancien (@+2P) 25 avril 2009 à 07:11 (CEST)
Réponse : En l'occurrence, il était bien difficile de ne pas citer de nom.
Je suis tombé un peu par hasard sur la page "sudoku" et ai été choqué par tout le passage sur les méthodes de résolution. J'ai été choqué ensuite que Farid Mita supprime le paragraphe sur les chaînes, alors que celles-ci sont la principale méthode de résolution des sudokus un peu complexes. Si je constate que l'on peut participer de manière constructive à Wikipedia sans tomber dans des conflits liés à des problèmes d'auto-glorification, je suivrai vos conseils et créerai un compte. En attendant de voir ce qui va sortir de votre signalisation du problème, je préfère me tenir à distance.— Le message qui précède, non signé, a été déposé par l'IP 92.140.82.217 (discuter)
- Je salue votre sagesse. N'ayez de crainte wikipedia est une encyclopédie qui a des règles consensuelles et rationnelles ( parfois malheureusement on hurle à la censure faute d'en respecter le fonctionnement ) Bien à vous --Neuromancien (@+2P) 25 avril 2009 à 07:45 (CEST)
- Réaction
Je ne fais pas de propagande! Puisque je n'ai rien à gagner!!D'autant plus que mes contributions sur wikipedia concernant le sudoku existaient depuis fin 2006, contributiosn que je peux classer en petits ajouts de précision dans certains passages de l'article puis en longs paragraphes, comme les degrés de difficulté, la typologie des grilles et les méthodes de résolution. Pour l'ISBN, sachez que le manuel a été publié au Maroc, et déposé à la Bibliothèque Nationale du Maroc avec un numéro de dépôt indiqué avec la référence. Et je n'ai pas assez d'argent pour faire publier mes manuels partout dans le monde! C'est pour cela que pour certaines personnes je reste un total inconnu dans le domaine du sudoku!! Je maintiens que la typologie que je propose en 5 degrés est plus pertinente que celle adoptée par les journaux et magazines et même les sites et gadgets, qui proposent des grilles "diaboliques" alors qu'elles sont de type 1 ou 2 ( faciles et résolubles mentalement) Certaines de leurs grilles ne sont même pas sudoku, c'est-à-dire qu'elles n'aboutissent pas à une seule solution! Enfin, je vous laisse le choix de supprimer mes contributions si vous jugez que je viens sur wikipédia juste pour m'autoglorifier! Dans ce cas, je ne contribuerai plus, voire supprimerai toutes les petites précisions que j'avais apportées. NB: Ne sous-estimez pas mon site perso! Je n'ai pas les moyens pour faire mieux! Et je n'ai pas de temps à perdre sur un tout petit problème qu'est le sudoku au détriment de mes recherches en mathématiques pures et dures puisque je suis avant tout, un mathématicien. Si le sudoku est devenu célèbre, ce n'est pas grâce à son aspet mathématique, mais parce que la plus part des gens l'ont trouvé attrayant et facile à résoudre! "Plus c'est populaire, plus c'est facile!" Sans rancune. --Farid mita (d) 25 avril 2009 à 16:25 (CEST)
- Donc vous n'êtes pas administrateur... En relisant les interventions j'ai été un peu surpris. Il est mal vu d'effacer de l'information sur les pages discussion en général et sur celle des autres en particulier. J'ai trouvé particulièrement déplacé que vous vous permettiez d'effacer la réponse de wanderer999 sur ma page de discussion alors que je ne l'avais même pas encore lue. Je vous remercie de ne plus le faire. Celà oblige à consulter l'historique et à faire de savantes comparaisons. De même j'ai pris du temps pour essayer de régler le conflit sur la page Sudoku ( je n'y interviens pas sauf pour lutter contre le vandalisme et j'ai au départ rétabli votre version mise à mal par un utilisateur anonyme qui vous mettez en cause personnellement parce que je pensai que vous étiez un administrateur a priori expérimenté... donc objectif . Vous avez préféré masquer mes observations et les interventions de wanderer999 ( qui est un administrateur des plus rigoureux) Ceci est assez pénible et ne facilite pas la gestion de ce conflit. Je vous conseille d'archiver éventuellement les messages en laissant un lien "vers les archives" et à réfléchir au fait que la discussion "n'est pas forcément close". MERCI DE TRAVAILLER CONJOINTEMENT. J'ai vu que vous aviez effacé votre nom de l'article c'est un bon début ... Cordialement--Neuromancien (@+2P) 27 avril 2009 à 14:15 (CEST)
Réponse à la réponse de Farid Mita.
Contrairement à ce que semble penser Neuromancien, vous êtes bel et bien administrateur de Wikipedia - c'est du moins ce qui apparaît sur votre page perso. Et cela bien que votre seule contribution soit celle sur le Sudoku, toujours d'après votre page perso. Il me semble que cela devrait vous éviter les débordements d'auto-glorification que vous nous avez donnés en spectacle. Il me semble aussi que cela jette un certain discrédit sur le choix par Wikipedia de ses administrateurs.
Si vous voulez discuter de vos idées, il y a pour cela de multiples forums spécialisés - et c'est gratuit. Votre présentation des 5 niveaux aboutit à des données statistiques (sans aucune indication de l'échantillon à partir duquel vous les avez obtenues) en contradiction flagrante avec toutes celles obtenues à partir d'échantillons aléatoires clairement définis - tout cela parce que vous n'avez jamais considéré que les puzzles les plus simples.
Votre section sur les chemins est incompréhensible. Elle ne décrit aucune des approches standard, qui utilisent des chaînes. Encore une fois, si vous avez des idées personnelles à défendre, faites-le sur les forums spécialisés. Sinon, rétablissez ce qu'un autre contributeur avait introduit brièvement à propos des chaînes et que vous avez abusivement supprimé.
Si vous restez un total inconnu dans le monde du Sudoku, ce n'est pas une question de manque d'argent, comme vous le prétendez, c'est en raison de votre non-participation aux forums sur le sujet - qu'on pourrait interpréter, avec un peu de malveillance, comme le refus de discuter de vos idées. Faites donc l'expérience, présentez vos 5 niveaux ou votre paragraphe sur les chemins, et prenez une bonne raclée. Après on en reparlera.
Signé 92.140.82.217 (au cas où mon IP aurait changé depuis la dernière fois).
- A monsieur l'anonyme 92.140 etc: je n'ai pas parlé de cinq niveaux, mais de cinq types dont chacun peut avoir plusieurs niveaux! Nuances mon vieux!! Puis, faut-il rappeler que la plupart des membres des forums viennent d'abord se ressourcer sur wikipedia avant de rédiger leur post sur les forums? Comment osez-vous qualifier ces membres de forums d'experts? --Farid mita (d) 13 mai 2009 à 00:43 (CEST)
- Réaction: Et voilà maintenant qu'on m'adresse des avertissements!! Il semble que je suis victime d'un certain utilisateur anonyme mais identifiable par ses IP, qui, au départ avait supprimé toute une partie de mes contributions sur le sudoku "vieilles" depuis plus de deux années et demie. Je reconnais avoir commis des erreurs, mais sans prémiditation puisque je ne pouvais en tirer un quelconque profit!! La première erreur, c'est d'avoir inséré mon nom d'auteur dans l'article même voulant protéger mes contributions! Ce qui a permis à l'utilisateur de m'attaquer, de vandaliser mes contributions, et de m'insulter même de façon grotesque! La deuxième erreur, c'était d'avoir ajouté dans ma page d'utilisateur la boîte indiquant que j'étais administrateur, alors que je sais que ce qualficatif n'est que technique et que c'est le résultat d'une élection! Mais vous savez tous que je n'ai jamais utilisé cette "position" pour nulle quelconque imposture, comme l'utilisateur anonyme aime me persécuter avec!!! Cependant, vous pouvez toujours garder l'oeil, comme vous dites sur l'article et sur moi, mais également sur cet auteur utilisateur anonyme qui n'a même pas un compte sur wikipedia et qui, à mon avis ne fait que répéter et relater des idées déjà évoquées ici et là dans l'article en question, considère des forums de discussion comme de références fiables alors que la plupart de ses membres viennent se ressourcer sur wikipedia, et enfin il insère les liens hypertextes à l'intérieur du texte, reconduisant les lecteurs à l'extérieur de wikipedia ( il fallait mettre ces liens en bas de page comme références). Alors, si vraiment vous croyez que je suis un imposteur et que je cherche à tirer profit de mes contributions sur l'article, je vous permets de supprimer mon compte, d'effacer toutes mes contributions et de bloquer mes IP, et ...--Farid mita (d) 13 mai 2009 à 00:43 (CEST)
Une autre remarque d'un passant sur cet article : je constate que vos guerre d'adition consistent à ajouter ou retirer de longs paragraphes ne comportant aucune référence. Je rappelle à l'ensemble des intervenants que les ajouts à Wikipédia doivent être _vérifiables_ ce qui implique de fournir des sources externes et de bonne qualité à l'appui de ceux-ci. C'est vrai en toutes situations, c'est très particulièrement vrai en situation conflictuelle. Touriste (d) 13 mai 2009 à 09:06 (CEST)
Protection[modifier le code]
Il me semblait pourtant avoir été clair, plus aucune modification de la part de Farid mita (d · c · b) et de 92.140.37.48 (d · c · b). On discute, on échange et on se met d'accord dans l'intérêt de l'article et dans le respect des règles en vigeur ici. Je ne juge pas les contributions pour savoir qui a raison ou tort. Le plus sage est de prendre quelques de « repos » sans contribuer sur WP pour relativiser l'importance de cet article dans votre vie réelle. Leag ⠇⠑⠁⠛ 13 mai 2009 à 11:20 (CEST)
- Je salue cette décision de protéger l'article! Mieux encore, je suggère de ne pas permettre aux utilisateurs anonymes qui n'ont pas de compte sur wikipedia de contribuer par de longs paragraphes sans aspect "encyclopédiste" et qui vandalisent les travaux des autres! --Farid mita (d) 13 mai 2009 à 14:03 (CEST)
- Ce n'est à vous de décider de ça. Beaucoup d'adresses IP contribuent de meilleur manière que les utilisateurs enregistrés. Leag ⠇⠑⠁⠛ 14 mai 2009 à 10:15 (CEST)
- Mais pas à la manière de 92.140.37.48 (d · c · b). Son comportement devient maladif!--Farid mita (d) 14 mai 2009 à 10:56 (CEST)
- Ce n'est à vous de décider de ça. Beaucoup d'adresses IP contribuent de meilleur manière que les utilisateurs enregistrés. Leag ⠇⠑⠁⠛ 14 mai 2009 à 10:15 (CEST)
Témoignages et arbitrage des utilisateurs[modifier le code]
Je propose d'ouvrir cette nouvelle sous-section pour trancher sur ce dernier "conflit" entre deux contributeurs:
Wikasterix[modifier le code]
Je suis un lecteur fervent des articles de WP. Je n'ai créé un compte que dernièrement pour apporter mon témoignage concernant l'article sudoku et la guerre d'édition qui s'est déclarée entre Farid Mita, un trèc ancien contributeur et un un utilisateur anonyme dont l'IP est volatile. Les deux monsieurs ont tort de se vandaliser mutuellement les contributions! Mais, c'est monsieur l'anonyme qui a commencé en premier, en supprimant d'un seul coup toute une section concernant le degré de difficulté, alors qu'il pouvait reformuler certains passages seulement tout en respectant le travail existant depuis plusieurs mois. Le seul argument de l'utilisateur anonyme est que dans les forums auxquels il se refère, Farid Mita n'y participe pas!! Ce n'est pas une condition pour pouvoir contribuer sur WP. D'autant plus que les forums ne peuvent être considérés comme sources fiables pour un article ensyclopédique; leurs membres ne sont pas forcément des experts en la matière. Je crois que, à cause de cet acte de vandalisme, Farid Mita a réagi pour protéger ses contributions, en supprimant la section relative aux règles et concepts généraux du jeu, en avançant que cette dernière n'apporte rien de nouveau: les règles ont été déjà expliquées bien au début de l'article, la minimalité recherchée pour les puzzles ou grilles a été largement développée dans la section concernant la construction des grilles entre autres, les références sont des forums donc non fiables, les liens hypertextes sont mal rédigés, ... Pour intimider Farid Mita, l'anonyme contributeur ne cesse de qualifier le premier d'imposteur. Il lui renonce même son savoir mathématique comme s'il le connaissait très bien ou vivait près de lui. Vous connaissez la suite de l'histoire... Ce que je propose:
- 1) revoir et reformuler la section concernant le degré de difficulté sans supprimer aucun sous-paragraphe (types):
- 2) effacer les statistiques présentées à la fin de cette section, car elles peuvent découler à partir d'un nombre limité de logiciels de génération de grilles
- 3) supprimer carrément la section relative aux règles et concepts généraux du jeu
- 4) ne permettre auncun lien pointant vers des forums
- 5) ajouter à l'article une nouvelle section ou créer une nouvelle page où l'on mettra la terminologie française relative au sudoku ( techniques, règles, procédés, etc...)
NB: ce témoignage a été déjà rédigé sur Projet: Mathématiques Le Thé Sudoku que DocteurCosmos trouve raisonnable. --Wikasterix (d) 16 mai 2009 à 12:46 (CEST)
- Merci Wikasterix et DocteurCosmos. J'appouve vos propositions, surtout les 3è, 4è et 5è.--Farid mita (d) 17 mai 2009 à 00:45 (CEST)
Problème de références[modifier le code]
Il semble bien que cet article se heurte à un grave problème de références et que toute la discussion/querelle tourne autour de ce problème, Faird Mita ignorant toute référence autre qu'à lui-même et s'acharnant à vandaliser toute autre référence qui permettrait de démontrer qu'il a tort.
La section "Bibliographie" mentionne seulement 2 livres et un article dans la revue "Pour la science". C'est bien peu.
Certains participants (qui ne connaissent pas le domaine) voudraient interdire toute référence au site Sudopedia et aux principaux forums de discussion sur le Sudoku, se privant ainsi d'une source considérable de connaissances. Ils ne proposent pas d'autres références (il y en a pourtant).
Tant que cette question des références ne sera pas réglée, il me semble que tout débat est vain (et je ne commenterai même pas la prise de position partiale du nouveau venu sous le pseudo Wikastérix - tout aussi anonyme qu'un IP-, puisque, de ce point de vue, elle n'apporte strictement rien au débat).
Il est bien évidemment absurde d'envisager de définir une terminologie française du Sudoku sans le préalable de ces références. A noter d'ailleurs qu'il suffirait de traduire en français le contenu du site Sudopedia, sans avoir a réinventer la roue.
Signé 92.140.37.48
- Deux livres plus un article c'est déjà pas mal pour sourcer un article.
- PS : merci de signer vos messages en tapant quatre tilde comme ceci : ~~~~. DocteurCosmos (d) 17 mai 2009 à 11:15 (CEST)
Ca serait pas mal si l'article s'y référait vraiment. Ce n'est malheureusement pas le cas pour les sections controversées (chemins, types, ...).
Merci pour l'indication sur l'usage des tildes.
92.140.92.147 (d) 17 mai 2009 à 11:24 (CEST) 92.140.37.48
- Et voilà monsieur l'IP 92.140. et baratin, que vous refusez les opinions des "nouveaux venus"! Car, vous croyez que vous êtes le seul à détenir la vérité.
- Ne vous arrive-t-il pas de vous demander pourquoi, il y a que deux références bibliographiques seulement? En tout cas, ce n'est pas à cause de la complexité du problème! Lequel étant élucidé depuis longtemps et n'intéresse plus personne, sauf les retardataires!
- Vous voyez, en venant ici, sur WP, vous commencez à apprendre des trucs; comme signer vos posts avec des tildes entre autres!!!
- Vous êtes même aveugle à ce qu'on écrit sur vous et votre mésaventure. Cherchez sur les pages de discussion des autres utilisateurs de WP. Je ne pourrai vous indiquer les liens ici, ni vous les copier/coller vu leur nombre. Un rappel de quelques unes de mes réponses inspirées des discussions des autres utilisateurs dans leurs pages perso:
- Désolé! Les sites dont il est question ne peuvent être pris pour références! Un forum n'est rien qu'une tartine! Et ce n'est pas une obligation de les visiter!!!--
- Le mot minimal est-il écrit dans les livres saints jusqu'au point où il est interdit de les changer? C'est de la mégalomanie tout ça!! Monsieur l'anonyme ne voit les choses que d'un seul angle, alors qu'un esprit cartésien essaie de les voir sous plusieurs aspects et proposer plusieurs approches.--
- Participer à un forum n'est pas une condition obligatoire pour contribuer sur WP! Vous dites n'importe quoi! Vous êtes dans le désaroi!!!--
- Sur ce, heureux de vous avoir rencontré monsieur l'anonyme! Vraiment, j'apprends des choses dans la vie! --Farid mita (d) 17 mai 2009 à 12:45 (CEST)
- M. Farid mita (d · c · b), il n'est toléré d'attaquer l'adresse IP comme vous le faites ci-dessus. Prendre les gens de haut avec des propos du genre : « vous commencez à apprendre des trucs » ne joue pas en votre faveur. Chacun apprend de nouvelles choses tous les jours. Il n'est pas non plus juducieux de répéter plusieurs fois la même chose. Ce que vous dites dans une section de cette discussion n'a normalement rien à faire dans une autre section. Si vous n'avez plus d'argument au point de vous répéter, autant ne rien dire plutôt que de complexifier les discussions et de ne pas faire avancer le débat. Merci Leag ⠇⠑⠁⠛ 17 mai 2009 à 13:47 (CEST)
- A l'IP qui ne me souhaite pas la bienvenue et qui m'accuse d'avoir pris position contre lui: J'ai bien dit qu'il fallait revoir et reformuler la section sur le degré de difficulté. La notion de chemin qui est bien différente de celle des chaînes offre une autre stratégie de résolution et reste efficace. Mais j'ai dit également de supprimer carrément la section relative aux règles et concepts généraux du jeu, car on a l'impression que vous voulez re-écrire un article à l'intérieur de l'article, tout en répétant ce qui a été dit! Tout le monde est d'accord sur le fait qu'un forum ne peut être considéré comme une référence même si ses membres sont des joueurs chevronnés! D'ailleurs je rejoins Farid mita (d · c · b) en réaffirmant qu'il n'existe point de puzzle non résoluble, manuellement même!
- Je suis d'accord avec vous Leag (d · c · b) que Farid mita (d · c · b) a commis et continue de commettre des imprudences car se sentant peut-être victime d'un vandalisme sauvage de la part de l'autre utilisateur IP (!?). Je crois que c'est le style de rédaction en langue française qui lui fait défaut! Ne vous vexez pas Farid mita (d · c · b); peut-être que j'écris bien mal que vous! Mais vous devez accepter que l'on reformule vos contributions et votre approche relative à la typographie. En revanche, toute la section des répétitions ( régles et concepts du jeu) ne doit pas exister sur l'article, encore moins les forums comme références.
- --Wikasterix (d) 17 mai 2009 à 15:49 (CEST)
Moi-même nouveau ici, je ne connaissais pas l'usage de se souhaiter la bienvenue, mais bienvenue, Wikastérix.
Vous êtes d'autant mieux le bienvenu que vous semblez en mesure de nous expliquer en quoi la "notion de chemin est bien différente de celle des chaînes". Parce que, d'après ce qu'a écrit Farid Mita, je ne comprends pas bien.
Et puis ce que signifie "résoluble manuellement".
92.140.92.147 (d) 17 mai 2009 à 18:00 (CEST)RésolumentAnonyme(92.140.37.48)
Proposition de réécriture[modifier le code]
Pour avancer concrètement, dans les quatre sections qui suivent ("Méthodes de résolution utilisées par les joueurs", "Classification des puzzles", "Solutions logicielles" et "Construction de grilles"), je propose une refonte complète de la fin de l'article - actuelles sections 8 à 12). Pour les actuelles sections 10 ("solutions logicielles") et 12 ("construction de grilles"), il ne s'agit que de remaniements légers. Pour les 3 autres, je ne pense pas qu'on puisse éviter une refonte complète.
J'ai séparé toute cette proposition de ce qui précède par deux lignes horizontales, avant et après, afin de l'identifier clairement. J'ai également introduit une section "Discussion de la proposition précédente" dont l'objectif est clairement d'éviter la vandalisation de la proposition.
Merci donc de ne pas faire de modification directement entre les séparateurs horizontaux.
Certains paragraphes sont indiqués [à compléter], ce que je me propose de faire si un accord est obtenu sur le principe de cette nouvelle rédaction.
J'ai librement réutilisé des passages existant, dus à plusieurs participants, sans chercher à attribuer ces passages à quiconque.
Puisque cela semble choquer, je n'ai mis aucune adresse des sites web, mais je mentionne Sudopedia, les principaux forums et les logiciels SudokuExplainer, sueg et d'autres, sans leurs adresses.
J'ai également ajouté à la bibliographie deux articles publiés dans des conférences scientifiques internationales, qui ont l'avantage par rapport au livre du même auteur d'être gratuitement accessibles sur le web. Je persiste cependant à penser qu'il faudrait des références supplémentaires, mais si l'on s'interdit ce qui n'est accessible que sur le web, je ne vois pas grand chose.
Si un administrateur décide de faire la substitution, pour que les références soient recopiées correctement, il faut copier à partir du mode "modification" ou "source" de cette page au mode "modification" de la page "article".
Méthodes de résolution utilisées par les joueurs[modifier le code]
Remarques préliminaires[modifier le code]
1) Il existe de nombreuses approches de la résolution des Sudokus, dont certaines ne sont praticables que par ordinateur. Il ne sera question ici que des méthodes utilisées par les joueurs.
2) Il ne s'agit pas de donner une liste exhaustive de ces méthodes (ce qui nécessiterait un livre volumineux), mais un simple aperçu. De nombreuses variantes et extensions existent, comme les poissons à arêtes (finned fish), trop spécialisées pour être détaillées ici.
3) Quelles méthodes de résolution sont-elles admissibles par un joueur ? Toute réponse à cette question ayant une composante subjective, ne pas reconnaître d'emblée ce fait ne pourrait que conduire à des querelles stériles. La plupart des joueurs refusent les essais et erreurs, ou hypothèses.
4) Il existe un site de référence, Sudopedia, présentant de manière consensuelle le vocabulaire standard du Sudoku et les règles de résolution les plus connues. En anglais uniquement, il fonctionne selon les mêmes principes que Wikipedia.
5) La notion de candidat n'est pas inhérente au problème du Sudoku, mais doit être introduite par le joueur pour mettre en œuvre la plupart des méthodes de résolution. Lorsqu'un chiffre n'est pas a priori impossible dans une cellule, on dit qu'il est candidat. Alors que les dévoilés sont les données initiales fixes d'un puzzle, l'ensemble des candidats évolue au cours du processus de résolution. Il ne peut que diminuer ; et cela se produit lorsqu'on a démontré (par les diverses méthodes décrites plus bas) qu'un candidat (qu'on ne savait jusque là pas encore impossible) est en fait impossible. Les fondements logiques formels de cette notion (qui n'est pas aussi évidente qu'il paraît) ont été définis et étudiés en détail dans "La logique cachée du Sudoku", un livre en anglais ("The Hidden Logic of Sudoku" [1])) ; ils font appel à la logique épistémique. L'article "From Constraints to Resolution Rules, Part I: Conceptual Framework"[2], librement disponible sur les pages web de son auteur, expose aussi cette logique dans le cadre général des problèmes de satisfaction de contraintes.
6) Comment introduire les candidats
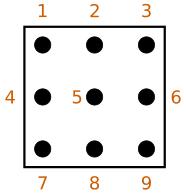
Il y a deux notations utilisées pour les candidats : indicée et pointée.
- Pour la notation indicée, les candidats sont inscrits dans une cellule, chaque chiffre occupant ou non une place précise. L'inconvénient de cette méthode est que les journaux publient des grilles de petite taille, ce qui rend difficile l'inscription de plusieurs chiffres dans une même cellule. Plusieurs joueurs reproduisent à plus grande échelle de telles grilles ou ont recours à un crayon à pointe fine.
- Pour la notation pointée, les joueurs inscrivent des points dans les cellules vides. La position relative du point indique le chiffre manquant. Par exemple, pour indiquer 1, un point apparaît en haut à gauche dans la cellule. Cette notation permet de jouer directement avec une grille imprimée dans un journal. Cependant, elle demande une certaine dextérité, il est possible de mal placer un point dans un moment d'inattention et une petite marque faite par erreur peut mener à de la confusion. Certains joueurs préfèrent utiliser un stylo pour limiter les fautes.
Essais et erreurs, ou hypothèses[modifier le code]
La méthode la plus rapide pour un ordinateur consiste à essayer systématiquement, l'un après l'autre, tous les candidats restant. Appliquée récursivement, elle peut résoudre tous les puzzles. Mais cette méthode, fort peu élégante, est rejetée par quasiment tous les joueurs. Tout au plus est-elle acceptée comme ultime recours, quand plus rien d'autre ne marche.
Règles élémentaires[modifier le code]
Quand un puzzle peut être résolu en n'utilisant que les règles élémentaires de cette section, des joueurs expérimentés peuvent se dispenser de l'écriture explicite des candidats.
propagation de contraintes élémentaires[modifier le code]
Si un nombre est affirmé comme étant nécessairement la valeur d'une cellule, supprimer tous les autres candidats de cette cellule et supprimer ce nombre comme candidat de toutes les autres cellules de la même ligne, de la même colonne et du même bloc.
singletons nus et cachés[modifier le code]
Singleton nu : si une cellule contient un unique candidate, alors c'est la valeur de cette cellule.
Singleton caché : si un candidat apparaît une fois et une seule sur une ligne (respectivement une colonne, un bloc), alors c'est la valeur de la cellule où il apparaît.
interactions ligne-bloc et colonne-bloc[modifier le code]
Si, sur une ligne L coupant un bloc B, un nombre n'apparaît pas comme candidat à l'extérieur de B, supprimer ce nombre comme candidat partout dans B sauf sur L.
Si, dans un bloc B coupé par une ligne L, un nombre n'apparaît pas comme candidat ailleurs que sur L, supprimer ce nombre comme candidat partout sur L à l'extérieur de B.
Si, sur une colonne C coupant un bloc B, un nombre n'apparaît pas comme candidat à l'extérieur de B, supprimer ce nombre comme candidat partout dans B sauf sur C.
Si, dans un bloc B coupé par une colonne C, un nombre n'apparaît pas comme candidat ailleurs que sur C, supprimer ce nombre comme candidat partout sur C à l'extérieur de B.
Méthodes basées sur des figures (patterns) simples prédéfinies[modifier le code]
Paires, triplets et quadruplets nus[modifier le code]
Paires nues sur une ligne : si, sur une ligne L, il existe deux cellules différentes qui ont pour candidats les mêmes deux nombres différents, alors supprimer ces deux nombres comme candidats de toutes les autres cellules de la ligne.
Paires nues sur une colonne : si, sur une colonne C, il existe deux cellules différentes qui ont pour candidats les mêmes deux nombres différents, alors supprimer ces deux nombres comme candidats de toutes les autres cellules de la colonne.
Paires nues dans un bloc : si, dans un bloc B, il existe deux cellules différentes qui ont pour candidats les mêmes deux nombres différents, alors supprimer ces deux nombres comme candidats de toutes les autres cellules du bloc.
Triplets (resp. quadruplets) nus sur une ligne : si, sur une ligne L, il existe 3 [resp. 4] cellules différentes qui ont tous leurs candidats parmi les mêmes 3 [resp. 4] nombres différents, alors supprimer ces 3 [resp. 4] nombres comme candidats de toutes les autres cellules de la ligne.
Triplets [resp. quadruplets] nus sur une colonne : si, sur une colonne C, il existe 3 [resp. 4] cellules différentes qui ont tous leurs candidats parmi les mêmes 3 [resp. 4] nombres différents, alors supprimer ces 3 [resp. 4] nombres comme candidats de toutes les autres cellules de la colonne.
Triplets (resp. quadruplets) nus dans un bloc : si, dans un bloc B, il existe 3 [resp. 4] cellules différentes qui ont tous leurs candidats parmi les mêmes 3 {resp. 4] nombres différents, alors supprimer ces 3 [resp. 4] nombres comme candidats de toutes les autres cellules du bloc.
Paires, triplets et quadruplets cachés[modifier le code]
Paires cachées sur une ligne : si, sur une ligne L, il existe deux cellules différentes qui ont deux candidats communs n'apparaissant pas ailleurs sur la ligne (chacune des 2 cellules pouvant avoir d'autres candidats), alors supprimer tous les autres candidats de ces deux cellules.
Paires cachées sur une colonne : si, sur une colonne C, il existe deux cellules différentes qui ont deux candidats communs n'apparaissant pas ailleurs sur la colonne (chacune des 2 cellules pouvant avoir d'autres candidats), alors supprimer tous les autres candidats de ces deux cellules.
Paires cachées dans un bloc : si, dans un bloc B, il existe deux cellules différentes qui ont deux candidats communs n'apparaissant pas ailleurs dans le bloc (chacune des 2 cellules pouvant avoir d'autres candidats), alors supprimer tous les autres candidats de ces deux cellules.
Triplets (resp. quadruplets) cachés sur une ligne : si, sur une ligne L, il existe 3 [resp. 4] cellules différentes qui ont 3 [resp. 4] candidats communs n'apparaissant pas ailleurs sur la ligne (chacune des 3 [resp. 4] cellules pouvant avoir d'autres candidats), alors supprimer tous les autres candidats de ces deux cellules.
Triplets [resp. quadruplets] cachés sur une colonne : si, sur une colonne C, il existe 3 [resp. 4] cellules différentes qui ont 3 [resp. 4] candidats communs n'apparaissant pas ailleurs sur la colonne (chacune des 3 [resp. 4] cellules pouvant avoir d'autres candidats), alors supprimer tous les autres candidats de ces deux cellules.
Triplets (resp. quadruplets) cachés dans un bloc : si, dans un bloc B, il existe 3 [resp. 4] cellules différentes qui ont 3 [resp. 4] candidats communs n'apparaissant pas ailleurs dans le bloc (chacune des 3 [resp. 4] cellules pouvant avoir d'autres candidats), alors supprimer tous les autres candidats de ces deux cellules.
Fish ou Poissons (X-Wing, Swordfish, Jellysfish)[modifier le code]
X-Wing en ligne : étant donné un nombre n, si, sur deux lignes différentes, il n'apparaît comme candidat que sur deux colonnes, le supprimer comme candidat partout sur les deux colonnes ailleurs que sur les deux lignes.
Swordfish en ligne : étant donné un nombre n, si, sur trois lignes différentes, il n'apparaît comme candidat que sur trois colonnes, le supprimer comme candidat partout sur les trois colonnes ailleurs que sur les trois lignes.
Jellyfish en ligne : étant donné un nombre n, si, sur quatre lignes différentes, il n'apparaît comme candidat que sur quatre colonnes, le supprimer comme candidat partout sur les quatre colonnes ailleurs que sur les quatre lignes.
Il existe bien entendu les règles homologues X-Wing en colonne, Swordfish en colonne et Jellyfish en colonne, dont l'énoncé est obtenu à partir des précédents en permutant les mots "ligne" et "colonne". (Mais il n'existe pas de règle pour les blocs).
Nota bene : il n'existe pas de règle homologue pour les blocs.
Symétries généralisées et tableau de résolution étendu[modifier le code]
Dans "The Hidden Logic of Sudoku"[1], basé sur une formalisation logique systématique du jeu, toutes ses symétries généralisées ont été explicitées, en particulier entre les lignes et les nombres, entre les colonnes et les nombres et entre les blocs et les nombres. Une nouvelle méthode de résolution a été développée, basée sur leur exploitation systématique. Les espaces rn, cn et bn (complémentaires de l'espace usuel rc) ont ainsi été introduits (p. 35 de la première édition). Une grille de résolution étendue a été conçue, qui fait apparaître les liens de conjugaison comme des cases (de l'espace rc, rn, cn ou bn) à deux candidats et peut faciliter l'application de la méthode. De la sorte, les sous-ensembles cachés, ainsi que les X-wings, Swordfish et Jellysfish, apparaissent tous comme de simples Paires, Triplets ou Quadruplets. Dans un cadre général pour traiter des chaînes, ces symétries ont été utilisées pour introduire de nouvelles règles de résolution, comme les chaînes xy cachées et ultérieurement les chaînes nrczt. Cette méthode a été implémentée dans un solveur, SudoRules, basé sur des techniques d'Intelligence Artificielle et simulant un joueur humain.
Remarque[modifier le code]
La liste de figures simples ci-dessus ne contient que les plus courantes. De nombreuses variantes et extensions existent, comme les poissons à nageoires (finned fish), trop spécialisées pour être détaillées ici.
Figures plus complexes : chaînes[modifier le code]
Quand les techniques d'élimination de candidats basées sur des figures (ou "patterns") simples ne suffisent pas, il faut recourir à des figures plus complexes, par exemple les chaînes. Une chaîne simple est une suite de candidats tels que chacun est lié au précédent. On peut définir plusieurs types de chaînes, qui peuvent tous être considérés comme des généralisations d'un unique type de base, la chaîne xy.
chaînes xy[modifier le code]
Une "chaîne xy" de longueur n a 2n candidats groupés par 2 dans n cellules bivaluées (c-à-d ayant chacune exactement 2 candidats).
Exemple de chaîne xy de longueur 4 : {a b} - {b c} - {c d} - {d a}. Un "{... }" symbolise le contenu d'une cellule (i.e. l'ensemble de ses candidats) et un "-" symbolise que les cellules de chaque côté sont liées (i.e. différentes mais sur la même ligne, la même colonne ou dans le même bloc).
Il est très facile de voir, par l'absurde, que tout nombre a dans une cellule n'appartenant pas à la chaîne mais liée à la fois à la première et à la dernière cellules de la chaîne peut être éliminé : si a était vrai dans cette cellule "cible", alors a serait faux dans la première cellule de la chaîne, dont la valeur ne pourrait donc être que b ; mais alors b serait faux dans la deuxième cellule, dont la valeur ne pourrait donc être que c ; ... ; on arriverait ainsi à la conclusion que la valeur de la dernière cellule de la chaîne ne pourrait être que a ; ce qui serait contradictoire avec le fait que a soit la valeur de la cellule cible.
Quand on a compris les chaînes xy et ce raisonnement, on a compris la logique inhérente à tous les types de chaînes.
Généralisations des chaînes xy : chaînes d'ALS et chaînes nrczt[modifier le code]
Parmi les généralisations logiques "naturelles" des chaînes xy, on a :
- les chaînes d'ALS (Almost Locked Sets), les plus anciennes et de loin les plus utilisées par les joueurs sur les forums de Sudoku ; un maillon de ces chaînes n'est plus un candidat mais un ALS (Almost Locked Sets), c-à-d un ensemble de k cellules (sur une même ligne, une même colonne ou dans un même bloc) dont les candidats appartiennent à un ensemble de k+1 nombres ;
- les chaînes xyt, xyz et xyzt ainsi que leurs homolgues "cachés" dans les espaces rn, cn et bn (définies dans la première édition de "The Hidden Logic of Sudoku") ; les chaînes nrczt, ou chaînes supersymétriques, qui généralisent les précédentes en combinant toutes les cellules des espaces rc, rn, cn et bn (définies dans la seconde édition de "The Hidden Logic of Sudoku"[1])) ;
- une combinaison des deux, dont on peut trouver de nombreux exemples sur le forum sudoku-factory.
Règles résultant de l'hypothèse d'unicité[modifier le code]
On exige en général d'un puzzle, qu'on dit alors bien formé, qu'il ait une solution et une seule. De toute évidence, cette exigence concerne d'abord le créateur de puzzles.
L'exigence qu'il y ait une solution ne pose pas de problème pour le joueur. Si elle n'est pas satisfaite par le créateur, le joueur pourra en général montrer la contradiction. Les règles mentionnées ci-dessus doivent en réalité s'interpréter de manière un peu plus subtile que sous la forme (usuelle) où elles ont été énoncées. La véritable interprétation est : "s'il y a une solution et si le candidat C est vrai, alors on a une contradiction". D'où l'on conclue "s'il y a une solution, alors C est faux", et on élimine C des candidats. De cette manière, si le puzzle est contradictoire, on est certain qu'on ne trouvera pas de solution.
L'exigence d'unicité est plus délicate. Elle s'impose au créateur, mais le joueur ne peut d'aucune façon la contrôler. En pratique, cela signifie que, si un puzzle qui a plusieurs solutions est proposé mais que le joueur applique des règles découlant de l'hypothèse d'unicité, il peut faire ainsi des éliminations non justifiées (et rater des solutions alternatives ou aboutir à une situation où il croit qu'il n'y a pas de solution). Ce problème tend à disparaître en pratique car les créateurs de puzzles vérifient désormais plus sérieusement l'unicité.
Le principe du rectangle interdit[modifier le code]
Considérons quatre cellules formant un rectangle s'étalant sur deux lignes, deux colonnes et seulement deux blocs. Si le contenu de ces quatre cellules est :
ab ab
ab ab
alors pour toute solution du puzzle ayant les valeurs
a b
b a
pour les cellules de ce rectangle, il existe une autre solution ayant les valeurs
b a
a b
et le puzzle ne peut donc avoir une solution unique.
La configuration initiale s'appelle rectangle interdit. A partir de là, on peut définir plusieurs règles visant à empêcher que cette situation se produise. Ces règles ne sont valables que sous l'hypothèse d'unicité.
Exemples de règle reposant sur l'exploitation du rectangle interdit[modifier le code]
Règle UR1 : dans la configuration (où les quatre cellules forment un rectangle s'étalant sur deux lignes, deux colonnes et seulement deux blocs) :
ab ab
ab abc
éliminer a et b de la dernière cellule.
Règle UR2-H : dans la configuration (où les quatre cellules forment un rectangle s'étalant sur deux lignes, deux colonnes et seulement deux blocs) :
ab abc
ab abc
où les deux cellules de droite sont dans le même bloc, éliminer c de toute autre cellule liée aux deux cellules de droite.
Il existe de nombreuses variantes de ces règles.
92.140.47.46 (d) 23 mai 2009 à 08:43 (CEST)RésolumentAnonyme
Classification des puzzles[modifier le code]
Il n'existe pas de classification universelle des différents puzzles : toute classification repose sur le choix d'un ensemble de méthodes de résolution. On peut cependant distinguer les classifications à large couverture (SER, SXT, NRCZT, etc.) et les classifications en quatre ou cinq niveaux (de "simple" à "diabolique"), comme ceux qui sont publiés dans les journaux. Ces dernières ne couvrent en général que des puzzles relativement simples, de SER ne dépassant pas 5 ou 6.
Il faut noter que chaque classification n'a de valeur qu'indicative et que, pour un joueur, deux puzzles ayant la même valeur dans une classification peuvent présenter des difficultés très différentes.
Préambule sur les puzzles minimaux et les statistiques de classification des puzzles[modifier le code]
Une notion générale très utile d'un point de vue théorique est celle de puzzle minimal. Un puzzle est dit minimal (ou, plus rarement, "localement minimal") s'il a une solution unique et si, chaque fois qu'on essaie de lui ôter un dévoilé, le puzzle obtenu (qui a toujours évidemment au moins une solution) se retrouve avoir plusieurs solutions.
Quand on veut faire des statistiques sur la classification des puzzles, il faut toujours se référer à des ensembles de puzzles minimaux, faute de quoi ces statistiques n'ont pas grand sens : en effet, en ajoutant autant de dévoilés qu'on veut, choisis parmi ses valeurs solutions, à un puzzle minimal, on peut obtenir de très nombreux puzzles qui auront évidemment la même solution, la plupart étant triviaux à résoudre.
A noter qu'il est très facile et rapide de générer par ordinateur des ensembles aléatoires de milliers de puzzles minimaux (avec, par exemple, le logiciel libre suexg. (Pour plus de détails sur la création de puzzles, voir plus loin).
La minimalité est une exigence annexe parfois attendue du créateur de puzzles. Elle est sans effet pour le joueur. Cependant elle peut être difficile à concilier avec d'autres exigences annexes, comme des exigences esthétiques, par exemple de symétrie, à savoir que les dévoilés se situent dans un ensemble de cellules présentant une certaine forme de symétrie. Il est plus difficile de générer des puzzles qui à la fois soient minimaux et aient certaines symétries (en particulier, suexg ne le fait pas).
SER (Sudoku Explainer Rating)[modifier le code]
Le SER (Sudoku Explainer Rating ) est de loin la classification la plus utilisée. "Sudoku Explainer" est un logiciel libre (en java), développé par Nicolas Juillerat et téléchargeable sur le web. Il peut être utilisé pour résoudre des puzzles mais aussi pour produire une estimation de leur difficulté, nommée leur SER. Celui-ci prend des valeurs de 1 à 11,7 (valeur maximale connue à ce jour).
Les règles qu'il utilise (dont certaines reposent sur l'hypothèse d'unicité) sont passablement hétérogènes et les valeurs affectées passablement ad hoc. A titre d'illustration, voici les niveaux associées à quelques unes des règles définies plus haut.
1.0 à 2.3 Divers singletons
3.0 Naked Pair
3.4 Hidden Pair
3.6 Naked Triplet
3.8 Swordfish
4.0 Hidden Triplet
5.0 Naked Quad
5.2 Jellyfish
5.4 Hidden Quad
11.6 Dynamic + Dynamic Forcing Chains (145-192 nodes) Cell Forcing Chains
11.7 Dynamic + Dynamic Forcing Chains (193-288 nodes) Double Forcing Chains
Ces "Dynamic Forcing Chains" sont une forme d' essais et erreurs.
Classification NRCZT[modifier le code]
Cette classification, définie dans "The Hidden Logic of Sudoku"[1], est basée sur la longueur maximale de la chaîne nrczt nécessaire pour résoudre un puzzle. Contrairement au SER, un seul type de règle (les chaînes nrczt de diverses longueurs) est ici utilisé et cette classification, purement logique, indépendante de l'hypothèse d'unicité et indépendante de toute implémentation, est compatible avec toutes les symétries du jeu.
Bien que reposant sur des règles qui sont donc fort différentes de celles à la base du SER, cette classification est étroitement corrélée à celui-ci : une étude faite sur 10.000 puzzles minimaux différents (obtenus avec le générateur pseudo-aléatoire suexg) donne un coefficient de corrélation est de 0,89. Cela signifie que ces deux classifications saisissent effectivement un aspect important de ce qui fait la complexité d'un puzzle.
Statistiques de la classification nrczt[modifier le code]
Ces statistiques sont disponibles dans le livre "The Hiden Logic of Sudoku" [1] ou l'article "From Constraints to Resolution Rules, Part II: chains, braids, confluence and T&E"[3] (sur la base de 10.000 puzzles minimaux aléatoires).
La répartition par niveaux nrczt de ces mêmes 10.000 puzzles se fait ainsi :
niveau 1 : 5.382
niveau 2 : 1.391
niveau 3 : 1.642
niveau 4 : 1.243
niveau 5 : 255
niveau 6 : 62
niveau 7 : 16
niveau 8 : 6
niveau 9 : 1
niveau 10 : 0
niveau 11 : 1
niveau 12 : 0
niveau 13 : 1
Sachant que la complexité effective d'un puzzle croît de manière quasi exponentielle avec son SER ou son NRCZT, ces chiffres montrent que :
1) une très grande majorité des puzzles peut se résoudre par des techniques relativement simples (ici, des chaînes courtes) ;
2) il reste malgré tout des puzzles de très grande complexité, ce qui justifie que les joueurs experts recherchent en permanence de nouvelles règles qui permettraient de simplifier les solutions obtenues avec les règles connues à ce jour ;
3) les puzzles exceptionnellement complexes (comme le fameux Easter Monster) ont très peu de chances d'être trouvés par un générateur aléatoire et certains joueurs essaient en permanence de créer de nouveaux exemples "à la main".
Classifications des puzzles "grand public"[modifier le code]
[Ce pourrait être la place pour une version très remaniée et raccourcie de la classification de Farid Mita]
92.140.47.46 (d) 23 mai 2009 à 08:47 (CEST)RésolumentAnonyme
- Je me suis permis de replacer une partie des contributions de Farid mita qui a été supprimée de l'article! Il paraît que depuis la "guerre d'édition" qu'a connu cet article, il ne vient plus sur wk(?!) bien que son adversaire-contributeur-anonyme 92.140.47.46 lui ai laissé une place dans ce paragraphe!
- Bien-sûr, les autres contributeurs sont invités à rectifier et reformuler cette partie...
- --Wikasterix (d) 15 juin 2009 à 13:56 (CEST)
Solutions logicielles[modifier le code]
Pour un informaticien, programmer la recherche d'une solution par le biais des contingences ou de multiples contingences (tel qu'exigé pour les problèmes les plus difficiles) est une tâche relativement simple. Un tel programme imite un joueur humain qui recherche une solution sans recourir au hasard.
Il est aussi relativement simple de concevoir un algorithme de recherche par backtracking. De façon habituelle, il suffit à l'algorithme de choisir 1 pour la première cellule, puis 2 pour la prochaine, ainsi de suite tant qu'aucune contradiction n'apparaît. Lorsqu'une contradiction apparaît, l'algorithme essaie une autre valeur pour la cellule qui amène la contradiction. Une fois toutes les possibilités épuisées pour cette cellule, l'algorithme « revient sur ses pas » et recommence avec l'avant-dernière cellule.
Bien que cet algorithme ne soit pas très élégant, il est certain de trouver une solution s'il en existe. Une grille 9×9 est habituellement résolue en moins de trois secondes avec un ordinateur personnel moderne qui a recours à un interpréteur, et en quelques millisecondes avec un langage compilé. Cependant, il existe des grilles qui sont particulièrement difficiles à résoudre par backtracking.Algorithmics of Sudoku#Solving sudokus by a brute-force algorithm
Une implémentation alternative du backtracking est de recourir à la programmation logique, telle qu'implantée dans Prolog. Dans ce cas, le concepteur fournit au programme les contraintes de la grille (un chiffre par rangée, par colonne et par région ; les chiffres dévoilés) ; ce programme prendra les décisions pour résoudre le problème. Si l'on admet que la grille a une solution unique, la recherche est certaine d'aboutir.
Donald Knuth a mis au point un algorithme qui fait appel aux listes doublement chaînées (les dancing links [4]), et qui se révèle très efficace pour résoudre ce type des Sudokus en quelques millisecondes.
Il existe aussi de nombreux programmes librement disponibles sur le web, basés sur l'implémentation de règles utilisées par les joueurs : Sudocue, Sudoku Explainer, Sudoku Susser, Sadman, le solveur de gsf. Le programme SudoRules, non public, est basé sur des techniques d'Intelligence Artificielle
Construction de grilles[modifier le code]
Il semblerait que les grilles de Dell Magazines, le pionnier dans le domaine de la publication, soient générées par ordinateur. Elles sont habituellement composées de 30 chiffres dévoilés répartis au hasard. L'auteur des grilles est inconnu. Durant l'hiver 2000, Wei-Hwa Huang a affirmé qu'il était l'auteur du programme qui génère ces grilles; selon lui, les grilles antérieures étaient construites à la main. Le générateur serait écrit en C++ et, bien qu'il offre certaines options pour satisfaire le marché japonais (symétrie et moins de chiffres), Dell préfère ne pas les utiliser. Certains spéculent que Dell continue à utiliser ce programme, mais aucune preuve ne soutient leur affirmation.
Les sudoku de Nikoli, important créateur de sudoku au Japon, sont construits à la main, le nom de l'auteur apparaissant avec chaque grille publiée ; les dévoilés sont toujours présentés de façon symétrique. Cet exploit est possible en connaissant à l'avance l'endroit où seront les dévoilés et en affectant par la suite un chiffre aux cellules ainsi choisies. Le Number Place Challenger de Dell affiche aussi le nom de l'auteur. Les grilles publiées dans la plupart des journaux britanniques seraient générées automatiquement, mais font appel à la symétrie, ce qui laisserait sous-entendre qu'un humain les crée. The Guardian affirme que ses grilles sont créées à la main par des Japonais, mais aucune mention de l'auteur n'est faite. Elles seraient construites par des gens de Nikoli. The Guardian a affirmé que puisqu'ils sont construits à la main, ils contiennent de « subtiles allusions » hautement improbables dans les grilles construites par ordinateur.
Il est possible de construire des grilles avec de multiples solutions ou sans solution, mais celles-ci ne sont pas considérées comme d'authentiques sudoku. Comme pour les autres jeux logiques, une solution unique est requise. Une grande attention est donc nécessaire lors de la construction d'une grille, puisqu'un seul chiffre mal placé risque de rendre la résolution de celle-ci impossible.
Le logiciel libre (suexg) permettant de construire des puzzles minimaux (plusieurs dizaines à la seconde) est disponible sur le Web.
La minimalité est une exigence annexe parfois attendue du créateur de puzzles, bien qu'elle soit sans effet pour le joueur. Elle peut être difficile à concilier avec d'autres exigences annexes, comme des exigences esthétiques, par exemple de symétrie, à savoir que les dévoilés se situent dans un ensemble de cellules présentant une certaine forme de symétrie. Il est plus difficile de générer des puzzles qui à la fois soient minimaux et aient certaines symétries (en particulier, suexg ne le fait pas).
Voir aussi[modifier le code]
Bibliographie[modifier le code]
- Narendra Jussien, Précis de Sudoku, Hermès Lavoisier, 2006, 188 pages (ISBN 2-7462-1559-4)
- Denis Berthier, The Hidden Logic of Sudoku, Lulu Publishers ; 1ère édition, Mai 2007, 384 pages (ISBN 978-1-84753-472-9); deuxième édition, Novembre 2007, 416 pages (ISBN 978-1-84799-214-7)
- « Le tsunami du sudoku », Pour la Science, n° 338, décembre 2005, p. 144.
- Denis Berthier, "From Constraints to Resolution Rules, Part I: Conceptual Framework", International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 08), December 5-13, 2008.
- Denis Berthier, "From Constraints to Resolution Rules, Part II: chains, braids, confluence and T&E", International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 08), December 5-13, 2008.
92.140.92.147 (d) 19 mai 2009 à 12:54 (CEST)RésolumentAnonyme
Discussion de la proposition précédente[modifier le code]
Réponse d'un ancien contributeur[modifier le code]
Je salue monsieur 92.140.92.147 pour le garnd travail de refonte de l'article qu'il vient de nous soumettre ici! C'est vraiement exceptionnel!
Je prie messieurs les administrateurs de bien vouloir débloquer l'article pour que cette nouvelle contribution de grande valeur scientifique y soit insérée.
Merci de m'avoir réservé une place dans la section intitulée Classifications_des_puzzles_commerciaux. Je vous laisse alors le soin de reformuler dans une langue "encyclopédique" ma contribution, sans ton familier ni prescripteur, mais sans me coller au dos le qualificatif de commercial!!
Merci d'avance et sans rancune. --Farid mita (d) 20 mai 2009 à 18:51 (CEST)
- Bravo Farid pour cette réplique courageuse! Après tout, Sudoku ne correspond pas à un " sujet très important au niveau universel"[...] comme l'a signalé Raziel (d · c · b) le 7 juin 2007 à 21:35 (CEST)!! --Wikasterix (d) 22 mai 2009 à 18:20 (CEST)
Merci pour vos réactions. J'ai complété la plupart des passages que j'avais préalablement indiqués comme "à compléter". Il reste à faire le dernier, je n'ai pas le temps maintenant, ce sera pour plus tard.
Il serait bon en effet que l'article soit débloqué afin qu'on puisse revenir à un fonctionnement normal.
Pour répondre à une remarque de Raziel, il est clair que le sudoku n'est pas un sujet "important au niveau universel". Mais la question n'est pas là : à partir du moment où l'article existe, autant l'écrire correctement et de manière consensuelle.
P.S. : Le mot "commercial" ne véhiculait dans mon esprit aucune connotation péjorative.
92.140.47.46 (d) 23 mai 2009 à 08:57 (CEST)RésolumentAnonyme
- Vu l'amélioration manifeste de l'ambiance et le consensus en ce sens, je lève la protection de l'article. Bonne continuation (on continue à regarder ce qui se passe bien sûr). Touriste (d) 23 mai 2009 à 09:09 (CEST)
- (en) Denis Berthier, « The Hidden Logic of Sudoku », Lulu Publishers, (ISBN 978-1-84753-472-9), (lire en ligne)
- Denis Berthier, "From Constraints to Resolution Rules, Part I: Conceptual Framework", International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 08), December 5-13, 2008
- Denis Berthier, "From Constraints to Resolution Rules, Part II: chains, braids, confluence and T&E", International Joint Conferences on Computer, Information, Systems Sciences and Engineering (CISSE 08), December 5-13, 2008
- Knuth: Preprints
Graphies[modifier le code]
Un sudoku, d’accord, mais des sudokus ou des sudoku ? Et un sudoku ou un sudoku ? Et un sudoku ou un Sudoku ?
L’article bénéficierait de plus de cohérence à cet égard… --Olivier1961 (d) 8 août 2010 à 18:55 (CEST)
Remarques mineures sur la section des remarques préliminaires (4.1)[modifier le code]
Je ne suis pas très familier de l'opportunité ou de la façon d'apporter certaines modifications sur wikipedia. Je vous fais donc part de deux impressions personnelles.
Il me semble qu'il faudrait passer la section 4.1 en format de liste (avec des # plutôt que des points numérotés à la main) ; mais il me semble aussi que le tout devient trop compact pour rester « digeste ».
Je me demande également s'il ne serait pas judicieux d'ajouter un lien externe direct vers sudopedia, dans le point 4. Ce lien étant par ailleurs disponible dans la section liens externes, je ne sais comment procéder pour « rapprocher » les deux. --Gourgouilloult (d) 7 janvier 2012 à 01:15 (CET)
- La question est de savoir si une numérotation est vraiment utile ? --TiboQorl (d) 7 janvier 2012 à 01:21 (CET)
C'est pas faux ! Concernant la section 4.2, il y a clairement trop de parenthèses, pour dire des choses généralement inutiles — comme celle qui dit : « (par les diverses méthodes décrites plus bas) » — ou d'un style clairement peu encyclopédique — exemple : « (qui n’est pas aussi évidente qu’il paraît) ».
« L’article […][24], librement disponible sur les pages web de son auteur, » : plutôt que dire qu'il est disponible, pourquoi ne pas directement faire un lien externe ? Lien qui pourrait être fourni dans la note de bas de page, mais ce n'est pas le cas.
Je vois qu'il y a déjà eu de grandes discussions sur la rédaction de cette article. N'ayant pas l'intention de lire tout le débat, je préfère ne pas toucher aussi « lourdement » à l'article. --Gourgouilloult (d) 7 janvier 2012 à 01:40 (CET)
Pertinence de la section : Sudoku algo (résolution)[modifier le code]
Le contenu de cette section pourrait être intéressant mais n'est pas sourcé, n'est pas rédigé correctement et n'est pas au bon endroit dans l'article... J'y ai apposé le bandeau idoine. Rowinner (discuter) 17 juillet 2017 à 17:01 (CEST)


