Trajectoire d'une comète

La trajectoire d'une comète est l'ensemble des positions successives d'une comète, calculées à l'aide de six paramètres.

Paramètres des trajectoires dans l'espace

La trajectoire d'une comète peut se définir dans l'espace selon six paramètres permettant de calculer très précisément la trajectoire complète. Deux de ces paramètres (excentricité orbitale et demi-grand axe) définissent la trajectoire dans un plan, trois autres (inclinaison, longitude du nœud ascendant et argument du périhélie) définissent l'orientation du plan dans l'espace et le dernier (instant de passage au périhélie) permet de calculer la position de la comète. Pour les détails, voir orbite.

Introduction aux coniques

Une conique est définie par trois paramètres :

• foyer ;
• droite directrice ;
• excentricité.

L'équation polaire générale d'une conique est : $r={\frac {p}{1+e\cos(\theta -\theta _{0})}}$.

L'excentricité définit le type de courbe :

• e = 0 : cercle ;
• 0 < e < 1 : ellipse ;
• e = 1 : parabole ;
• e > 1 : hyperbole.

Fig. 1 - Coniques.

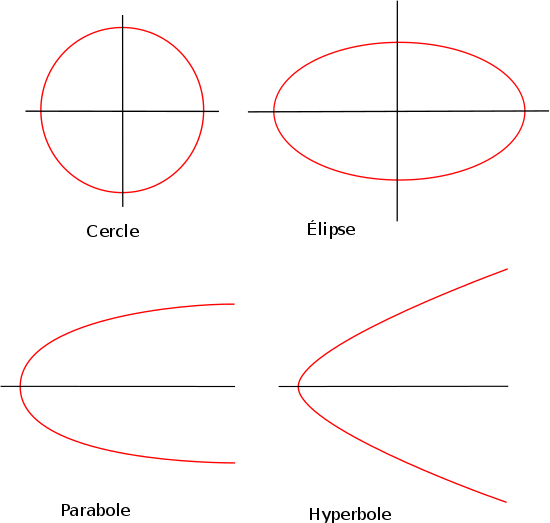
Un type de conique : les ellipses. (On peut appliquer ce qui est décrit dans ce paragraphe aux cercles.) Les ellipses sont donc des coniques dont l'excentricité e ∈ ]0;1[. On distingue pour une ellipse les paramètres suivants (voir la figure 2) :

• le centre C ;
• les deux foyers S et S', symétriques l'un de l'autre par rapport au centre C ;
• le grand axe de longueur 2a (et donc le demi-grand axe de longueur a). C'est un segment de la droite directrice ;
• le petit axe de longueur 2b (et donc le demi-petit axe de longueur b).

Fig. 2 - Ellipse.

Soient e l'excentricité, a le demi-grand axe et b le demi-petit axe, on a les égalités suivantes :

e = ${\frac {\sqrt {a^{2}-b^{2}}}{a}}$

a = ${\frac {b}{\sqrt {1-e^{2}}}}$

b = $a\times {\sqrt {1-e^{2}}}$

Application aux comètes

On peut désormais distinguer deux familles de comètes :

• les comètes dont la trajectoire est circulaire ou elliptique sont cycliques ;
• les comètes dont la trajectoire est parabolique ou hyperbolique, au contraire, ne reviennent jamais, leur trajectoire se prolonge à l'infini (sauf si un autre objet, Soleil excepté, suffisamment massif les dévie).

Nous nous limiterons ici à l'étude des trajectoires elliptiques (voir fig. 3).

Fig. 3 - Trajectoire elliptique d'une comète.

Il existe pour l'étude des trajectoires de comètes trois lois essentielles : les lois de Kepler.

• Première loi de Kepler : dans le référentiel héliocentrique, le Soleil occupe toujours l'un des deux foyers de la trajectoire des objets (planètes et comètes) qui gravitent autour.
• Seconde loi de Kepler : si S est le Soleil et M une position quelconque d'une comète, l'aire balayée par le segment [SM] entre deux positions C et D est égale à l'aire balayée par ce segment entre deux positions E et F si la durée qui sépare les positions C et D est égale à la durée qui sépare les positions E et F (voir Fig. 4).

Fig. 4 - Seconde loi de Kepler.

• Troisième loi de Kepler : soient T la période d'une comète (temps entre deux passages successifs au périhélie) et a le demi-grand axe de la trajectoire de ladite comète : a³ / T² = k avec k constant et k=1 si T est exprimée en années et a en unités astronomiques (1 UA = distance Terre-Soleil). D'où : a = ³√(T²) = T^2/3 si T est exprimée en années et a en UA.

Cette formule ainsi que les formules de l'ellipse permettent de calculer les différents paramètres d'une trajectoire elliptique à partir de très peu d'informations. Chaque point de l'ellipse peut ensuite être déterminé par la formule SM+S'M=2a où S et S' sont les deux foyers de l'ellipse et M le point que l'on cherche à déterminer.

Position d'une comète en fonction du temps

Considérons la figure 5. Le cercle de centre C et de rayon a est le cercle principal des ellipses de centre C et de demi-grand axe a. M est un point de l'ellipse considérée et M' le point du cercle principal (cercle dont le centre est le centre de l'ellipse et dont le rayon est égal au demi-grand axe) tel que la droite (MM') soit perpendiculaire au grand axe de l'ellipse et que le segment [MM'] ne coupe pas le grand axe. E est l'angle orienté (CP;CM') (CP et CM' sont des vecteurs) et est appelé anomalie excentrique de M. Soit T la période de la comète, τ l'instant de passage au périhélie et t un instant donné, on a la formule suivante : E - e sin(E) = (2π / T) (t-τ)

Cette équation, dite équation de Kepler, permet de déterminer à tout moment l'anomalie excentrique E de la position d'une comète et donc cette position.

Fig. 5 - Position d'une comète à un instant donné.

Vitesse d'une comète

On peut estimer la vitesse d'une comète entre deux points de sa trajectoire grâce à la seconde loi de Kepler. Par exemple, la vitesse de passage à l'aphélie est inférieure à la vitesse de passage au périhélie et la différence est d'autant plus grande que l'ellipse est allongée (c'est-à-dire que l'excentricité est élevée). Cela se démontre aisément : Soient A, B, C et D quatre points de l'ellipse tels que A et B soient très proches du périhélie et C et D de l'aphélie, si l'arc de l'ellipse délimité par A et B et celui délimité par C et D sont égaux, l'aire ainsi définie par le premier arc et le foyer correspondant au Soleil sera beaucoup plus petite que celle définie par le second arc et le même foyer, d'autant plus que l'ellipse sera allongée. Selon la seconde loi de Kepler, la durée mise par la comète pour aller de A à B sera donc beaucoup plus petite que celle mise pour aller de C à D (pour une distance pourtant égale). La vitesse entre A et B sera donc beaucoup plus grande que la vitesse entre C et D.

Des formules complexes — dont nous ne traiterons pas — permettent de calculer très exactement la vitesse ou l'accélération d'une comète en un point de sa trajectoire (ces formules sont bien plus simples dans le cas de trajectoires circulaires mais seules les planètes et certaines comètes ont des trajectoires s'approchant d'un cercle). Toutes ces formules permettant d'étudier les comètes avec une grande précision permettent également d'améliorer notre connaissance du système solaire, par la mesure des variations éventuelles entre le modèle mathématique et les observations expérimentales.

Paramètres de quelques comètes

Voici quelques-uns des paramètres de quelques comètes connues. Il s'agit uniquement des paramètres concernant l'étude dans un plan.

Comète	Période T (a)	Excentricité e	Demi-grand axe a (ua)	Demi-petit axe b (ua)
2P/Encke	3,298 45	0,847 45	2,215 85	1,176 34
C/1975 V1 (West)	6,12	0,582	3,345 81	2,720 77
3D/Biela	6,620 79	0,755 92	3,525 93	2,308 3
108P/Ciffréo	7,23	0,543 173	3,739 03	3,139 37
13P/Olbers	72,405	0,930 97	17,371 8	6,342 38
1P/Halley	76,028 8	0,967 28	17,946 7	4,553 29
109P/Swift-Tuttle	135,1	0,963 589	26,329 2	7,040 09
C/2004 F4 (Bradfield) (de)	293	0,987 6	44,114 2	6,925 54
C/1969 Y1 (Bennett)	1678	0,996 2	142,44	12,405 8
C/1995 O1 (Hale-Bopp)	2380	0,994 972	178,259	17,853 3
C/1908 R1 (Morehouse)	∞	1,000 7	∞	∞

Orbite de trois comètes représentatives des principales familles regroupant ces corps mineurs ː
- La comète 67P/Churyumov–Gerasimenko de la famille des comètes de Jupiter caractérisée par un demi grand axe de 3,457 Unités Astronomique (U.A.), une période de 6,44 ans années et un périhélie situé à 1,21 U.A du Soleil.
- La comète de Halley de la famille éponyme caractérisée par un demi grand axe de 17,737 U.A. , une période de 74,7 ans années et un périhélie situé à 0,597 U.A du Soleil.
- La comète de longue période C/2006 Q1 McNaught caractérisée par un demi grand axe de 6890 U.A. , une période de 575 223 années et un périhélie situé à 2,77 U.A.
Les dimensions, la forme et la position du périhélie et de l'aphélie des orbites des comètes est proche des valeurs réelles par contre la direction du grand axe a été choisie pour permettre une présentation plus lisible.