Algèbre géométrique (structure)

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.

L'article doit être débarrassé d'une partie de son jargon (mars 2017).

Sa qualité peut être largement améliorée en utilisant un vocabulaire plus directement compréhensible. Discutez des points à améliorer en page de discussion.

Une algèbre géométrique est, en mathématiques, une structure algébrique, similaire à une algèbre de Clifford réelle, mais dotée d'une interprétation géométrique mise au point par David Hestenes, reprenant les travaux de Hermann Grassmann et William Kingdon Clifford (le terme est aussi utilisé dans un sens plus général pour décrire l'étude et l'application de ces algèbres : l'algèbre géométrique est l'étude des algèbres géométriques). Le but avoué de ce physicien théoricien et pédagogue est de fonder un langage propre à unifier les manipulations symboliques en physique, dont les nombreuses branches pratiquent aujourd'hui, pour des raisons historiques, des formalismes différents (tenseurs, matrices, torseurs, analyse vectorielle, utilisation de nombres complexes, spineurs, quaternions, formes différentielles…). Le nom choisi par David Hestenes (geometric algebra) est celui que Clifford voulait donner à son algèbre.

L'algèbre géométrique se veut utile dans les problèmes de physique qui impliquent des rotations, des phases ou des nombres imaginaires. Ses partisans disent qu'elle fournit une description plus compacte et intuitive de la mécanique quantique et classique, de la théorie électromagnétique et de la relativité. Les applications actuelles de l'algèbre géométrique incluent la vision par ordinateur, la biomécanique ainsi que la robotique et la dynamique des vols spatiaux.

Histoire[modifier | modifier le code]

Dès l'Antiquité des liens entre l'algèbre et la géométrie étaient connus des Grecs, mais les bases du système dont il est ici question furent établies au XIX^e siècle.^{[réf. nécessaire]}

En 1843 William Rowan Hamilton découvre les quaternions qu'il interprète géométriquement comme des vecteurs (à tort). Un an plus tard, Hermann Günther Grassmann introduit le produit intérieur et le produit extérieur qui permettent la construction d'algèbres opérant sur des objets géométriques. Enfin, en 1873 William Kingdon Clifford parvient à intégrer les résultats d'Hamilton et ceux de Grassmann dans une première formulation de l'algèbre géométrique.

La découverte de Clifford passe inaperçue, sans doute à cause du décès prématuré de son auteur,^{[réf. nécessaire]} et les physiciens de la fin du XIX^e siècle ne connaissant pas cet outil mathématique commencent à employer un autre système connu sous le nom de « calcul vectoriel ». Développé par Josiah Willard Gibbs et Oliver Heaviside, le calcul vectoriel a permis notamment de formuler clairement la théorie de l'électromagnétisme de James Clerk Maxwell, et s'est également révélé d'usage facile en mécanique classique. Ces succès en ont fait, jusqu'à ce jour, le système mathématique le plus utilisé en physique.

Au début du XX^e siècle, la théorie de la relativité générale amène à reconnaître l'espace-temps de dimension 4. Le calcul vectoriel ne s'étend pas bien en dimension 4, une des raisons étant que le produit vectoriel n'est défini qu'en dimension 3. Les physiciens, n'ayant toujours pas connaissance des algèbres découvertes par Clifford, compensent les insuffisances du calcul vectoriel en introduisant divers systèmes mathématiques complémentaires.

Ce n'est que dans la deuxième moitié du XX^e siècle que David Hestenes montra que l'algèbre géométrique est parfaitement adéquate en dimension 4 où elle se décline en algèbre de l'espace-temps (Space-Time Algebra) qui formalise élégamment et efficacement la relativité restreinte. Hestenes montre également qu'avec l'algèbre géométrique, l'électromagnétisme gagne en simplicité, et que la mécanique classique en dimension 3 bénéficie d'une meilleure gestion des rotations. Un autre résultat majeur obtenu par Hestenes est que la mécanique quantique peut être reformulée par l'algèbre géométrique sans nombres imaginaires et sans matrices, avec une interprétation géométrique.

Aujourd'hui, l'algèbre géométrique est présentée par ses défenseurs comme langage universel pour les ingénieurs et physiciens. Leurs arguments sont solides, mais le poids de l'histoire s'oppose à la refondation qu'ils proposent et leur cause ne progresse que lentement.^{[réf. nécessaire]}

Définitions[modifier | modifier le code]

Algèbre géométrique[modifier | modifier le code]

Il existe plusieurs définitions d'une algèbre géométrique, mais l'une des plus concises peut-être formulée ainsi:

Définition — Une algèbre géométrique est une algèbre associative unitaire sur un corps, engendrée par un sous-espace vectoriel^[1] dont tous les éléments ont pour carré un scalaire^[2].

Avec cette définition, l'algèbre géométrique, le corps et le sous-espace vectoriel sont notés respectivement ${\mathcal {G}}$ , $\mathbb {K}$ ^[3] et ${\mathcal {V}}$ . La principale condition exprimée dans la définition s'écrit alors: $\forall \mathbf {v} \in {\mathcal {V}},\,\mathbf {v} ^{2}\in \mathbb {K}$ .

Hestenes a exprimé sa forte réticence à considérer le cas d'une algèbre sur le corps des complexes^[4]. En fait, dans Hestenes, Li et Rockwood 2001, le corps des scalaires est bel et bien choisi égal au corps des réels. La définition la plus générale a ici été présentée mais dans le reste de cet article, sauf mention contraire, on supposera $\mathbb {K} =\mathbb {R}$ . Dans ce même ouvrage, Hestenes impose aussi à ${\mathcal {V}}$ une dimension finie $n$ . Dans ce cas, ${\mathcal {V}}$ et ${\mathcal {G}}$ peuvent être notés respectivement ${\mathcal {V}}^{n}$ et ${\mathcal {G}}_{n}$ (ou ${\mathcal {G}}({\mathcal {V}}^{n})$ ).

Dans cet article, ${\mathcal {V}}$ est de dimension quelconque, mais dans le cas où cette dimension est infinie, elle sera tout de même supposée dénombrable pour faciliter les notations.

L'opération de multiplication dans une algèbre géométrique est appelée produit géométrique. Elle est le plus souvent notée sans symbole, par simple juxtaposition des opérandes. Cependant certains auteurs, notamment Eric Lengyel (en), préconisent l'utilisation du symbole unicode U+27D1 : ⟑ .

Lorsque ${\mathcal {V}}$ est de dimension finie, et que le carré de tout élément de ${\mathcal {V}}$ est positif, il sera vu plus loin que ${\mathcal {V}}$ est alors dotée d'une structure d'espace vectoriel euclidien. On pourra alors parler de « cas euclidien ».

Algèbre de Clifford[modifier | modifier le code]

La donnée d'un espace vectoriel ${\mathcal {V}}$ et d'une forme quadratique ${\mathcal {Q}}$ sur ${\mathcal {V}}$ permet de construire une algèbre géométrique dite générée par ${\mathcal {V}}$ sous la condition $v^{2}={\mathcal {Q}}(v)$ . Cette algèbre est ce qu'on appelle l'algèbre de Clifford.

Si une algèbre de Clifford requiert une forme quadratique pour sa définition, on verra plus loin qu'inversement, une algèbre géométrique permet de définir de façon unique une forme quadratique à partir du produit géométrique. La notion d'algèbre géométrique est donc identique à celle d'algèbre de Clifford, la seule différence étant l'ordre de présentation : une algèbre de Clifford est définie à partir d'un espace vectoriel et d'une forme quadratique, tandis qu'une algèbre géométrique est définie à partir d'une algèbre et d'un sous-espace vectoriel particulier. C'est pourquoi de nombreuses sources définissent purement et simplement les algèbres géométriques comme des algèbres de Clifford, assimilant exactement les deux concepts.

Vecteur[modifier | modifier le code]

Même si ${\mathcal {G}}$ est en tant qu'algèbre doté d'une structure d'espace vectoriel, David Hestenes réserve le mot vecteur aux éléments de ${\mathcal {V}}$ . Dans cet article, en règle générale, les vecteurs seront notés en bas-de-casse gras.

Produits intérieur et extérieur[modifier | modifier le code]

À partir du produit géométrique de deux vecteurs $a$ et $b$ , on définit deux nouveaux produits, dont le premier est symétrique et le second antisymétrique^[5]:

{\begin{aligned}\mathbf {a} \cdot \mathbf {b} &={\frac {1}{2}}\left(\mathbf {a} \mathbf {b} +\mathbf {b} \mathbf {a} \right)\\\mathbf {a} \wedge \mathbf {b} &={\frac {1}{2}}\left(\mathbf {a} \mathbf {b} -\mathbf {b} \mathbf {a} \right)\end{aligned}}

$a • b$ est appelé produit intérieur, $a \land b$ est appelé produit extérieur. La littérature scientifique francophone utilise aussi le chevron ( $\land$ ) pour désigner le produit vectoriel. Cette ambiguïté n'existe pas dans la littérature anglo-saxonne car le produit vectoriel y est désigné par le symbole $\times$ .

Théorème — Le produit intérieur de deux vecteurs est un scalaire

\mathbf {a} \cdot \mathbf {b} \in \mathbb {K}

Démonstration :

\mathbf {a} \cdot \mathbf {b} ={\frac {1}{2}}(\mathbf {a} \mathbf {b} +\mathbf {b} \mathbf {a} )={\frac {1}{2}}((\mathbf {a} +\mathbf {b} )^{2}-\mathbf {a} ^{2}-\mathbf {b} ^{2})\in \mathbb {K}

Le produit extérieur est généralisé à $k$ vecteurs par la formule suivante :

\bigwedge _{j=1}^{k}\mathbf {a} _{j}=\mathbf {a} _{1}\wedge \mathbf {a} _{2}\wedge \dots \wedge \mathbf {a} _{k}={\frac {1}{k!}}\sum _{\sigma \in {\mathfrak {S}}_{k}}\operatorname {sgn} (\sigma )\mathbf {a} _{\sigma (1)}\mathbf {a} _{\sigma (2)}\dots \mathbf {a} _{\sigma (k)}

où ${\mathfrak {S}}_{k}$ est le groupe des permutations d'indice $k$ .

Il sera vu plus loin que le produit intérieur correspond au produit scalaire usuel. Quant au produit extérieur, bien que ce n'est pas démontré dans cet article, il correspond au produit extérieur tel que définit dans l'article algèbre extérieure. Cette identité justifie l'utilisation de la même terminologie et de la même notation.

Décomposition canonique[modifier | modifier le code]

Pour deux vecteurs $a$ et $b$ , on a la relation suivante, qui constitue la décomposition dite canonique du produit géométrique de deux vecteurs :

\mathbf {ab} =\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} .

$\mathbf {a} \cdot \mathbf {b}$ et $\mathbf {a} \wedge \mathbf {b}$ sont respectivement appelés partie scalaire et partie bivectorielle du produit géométrique $ab$ . Cette terminologie est justifiée par les observations précédentes, quant à la nature des produits intérieurs et extérieurs.

Multivecteur[modifier | modifier le code]

Les éléments de ${\mathcal {G}}$ sont appelés multivecteurs. Hestenes utilise aussi parfois l'expression directed number, qu'on peut traduire par nombre orienté. Cependant, le terme multivecteur semble prévaloir dans les publications récentes.

Verseur[modifier | modifier le code]

Un verseur (versor en anglais) est un multivecteur qui peut être écrit comme produit géométrique de vecteurs non nuls. Le nombre de vecteurs formant par produit géométrique un verseur donné est minoré par ce qu'on appelle son grade.

Comme il sera vu plus loin dans cet article, les verseurs sont à la base de la plupart des applications de l'algèbre géométrique, car leur exponentiation permet de générer notamment les isométries dans le cas euclidien.

Base canonique[modifier | modifier le code]

Une base canonique est une base de ${\mathcal {G}}$ (vu en tant qu'espace vectoriel) telle qu'il existe une base orthonormée $(\mathbf {e} _{1},\mathbf {e} _{2},...)$ de ${\mathcal {V}}$ dans laquelle les éléments de la base canonique peuvent s'écrire^[6] :

e_{J}=\mathbf {e} _{\sigma _{1}}\mathbf {e} _{\sigma _{2}}\ldots \mathbf {e} _{\sigma _{k}}

où $J=(\sigma _{1},\sigma _{2}\ldots \sigma _{k})$ est une suite finie et strictement croissante d'entiers positifs.

Dimension finie[modifier | modifier le code]

Les définitions de cette sous-section ne sont valables que lorsque ${\mathcal {V}}$ est de dimension finie $n$ .

Pseudoscalaire[modifier | modifier le code]

Un pseudoscalaire est un verseur dont le grade $n$ est égal à la dimension de l'espace. Tous les pseudoscalaires sont multiples les uns des autres, c'est-à-dire que $\mathrm {dim} {\mathcal {G}}_{n}=\mathrm {dim} {\mathcal {G}}_{0}=1$

Tous les pseudoscalaires unitaires^[7], notés $I_{\sigma }$ , sont égaux à un signe moins près. Cette quasi-unicité justifie une notation indépendante du choix des vecteurs $\mathbf {\sigma }$ , ainsi que l'utilisation de l'article défini.

Le pseudoscalaire unitaire est donc défini par :

I=\pm I_{\sigma }

Dualité[modifier | modifier le code]

La dimension finie permet de fixer une dualité, et avec elle un opérateur d'intersection ( $\vee$ ) tel que l'intersection de deux multivecteurs est, à un facteur de proportionnalité près, le dual du produit extérieur des duaux.

Il existe plusieurs choix de dualité, comme la dualité de Poincaré et la dualité de Hodge.

Analyse multivectorielle[modifier | modifier le code]

Article détaillé : analyse multivectorielle.

Tout comme la donnée d'un espace vectoriel permet l'analyse vectorielle, c'est-à-dire l'étude du calcul infinitésimal pour des fonctions définies sur cet espace vectoriel à valeurs scalaires ou vectorielles, la donnée d'une algèbre géométrique, dont les éléments sont appelés multivecteurs, permet l'analyse dite multivectorielle des fonctions définies sur ${\mathcal {V}}$ mais à valeurs cette fois potentiellement multivectorielles. Les anglo-saxons, à l'instar d'Hestenes, parlent de geometric calculus ou multivector calculus, tout comme ils parlent de vector calculus pour désigner ce que les francophones appellent analyse vectorielle.

Propriétés[modifier | modifier le code]

Symétrie et antisymétrie des produits intérieur et extérieur[modifier | modifier le code]

Les produits intérieur et extérieur de deux vecteurs sont, par construction, respectivement symétrique et antisymétrique :

{\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=\mathbf {b} \cdot \mathbf {a} \\\mathbf {a} \wedge \mathbf {b} &=-\mathbf {b} \wedge \mathbf {a} \end{aligned}}

Plus généralement, le produit extérieur de plusieurs vecteurs est antisymétrique :

\forall \sigma \in {\mathfrak {S}}_{k},\quad \bigwedge _{j=1}^{k}\mathbf {a} _{j}=\operatorname {sgn} (\sigma )\bigwedge _{j=1}^{k}\mathbf {a} _{\sigma (j)}

Caractérisation algébrique de notions géométriques[modifier | modifier le code]

Colinéarité et orthogonalité[modifier | modifier le code]

Théorème — Deux vecteurs sont colinéaires si et seulement si leur produit extérieur est nul.

Démonstration

Si deux vecteurs $\mathbf {a}$ et $\mathbf {b}$ sont colinéaires, alors il existe un scalaire $\lambda$ tel que $\mathbf {a} =\lambda \mathbf {b}$ . Dès lors, on a $\mathbf {a} \wedge \mathbf {b} =\lambda \mathbf {a} \wedge \mathbf {a} =\lambda 0=0$ .

Inversement, si $\mathbf {a} \wedge \mathbf {b} =0$ , alors la décomposition canonique donne $\mathbf {a} \mathbf {b} =\mathbf {a} \cdot \mathbf {b}$ . En multipliant à droite par $\mathbf {b}$ , il vient $\mathbf {a} \mathbf {b} ^{2}=(\mathbf {a} \cdot \mathbf {b} )\mathbf {b}$ et donc, en ignorant le cas dégénéré où $\mathbf {b} ^{2}=0$ :

$\mathbf {a} ={\frac {\mathbf {a} \cdot \mathbf {b} }{\mathbf {b} ^{2}}}\mathbf {b} .$

Il reste alors à observer que ${\frac {\mathbf {a} \cdot \mathbf {b} }{\mathbf {b} ^{2}}}$ est un scalaire en tant que quotient de deux scalaires. Il y a donc bien colinéarité.

Cette observation, ajoutée à la définition de l'orthogonalité, permet de déduire les deux propriétés fondamentales suivantes :

Caractérisation algébrique de l'orthogonalité et de la colinéarité —

Deux vecteurs sont orthogonaux si et seulement si ils anti-commutent.
Deux vecteurs sont colinéaires si et seulement si ils commutent.

C'est-à-dire^[8] :

{\begin{array}{ccccc}\mathbf {a} \perp \mathbf {b} &\iff &\mathbf {a} \cdot \mathbf {b} =0&\iff &\mathbf {a} \mathbf {b} =-\mathbf {b} \mathbf {a} \\\mathbf {a} \propto \mathbf {b} &\iff &\mathbf {a} \wedge \mathbf {b} =0&\iff &\mathbf {a} \mathbf {b} =\mathbf {b} \mathbf {a} \end{array}}

Indépendance linéaire[modifier | modifier le code]

Une généralisation de la caractérisation algébrique de la colinéarité existe pour l'indépendance linéaire. En effet, $k$ vecteurs $(\mathbf {a} _{1},\mathbf {a} _{2}\ldots ,\mathbf {a} _{k})$ sont linéairement indépendants si et seulement si leur produit extérieur est non nul. Ou, de façon équivalente, ils sont linéairement dépendants si et seulement si leur produit extérieur est nul :

\left(\exists (\alpha _{1},\alpha _{2}\ldots ,\alpha _{k})\in \mathbb {K} ^{k}\setminus \{(0,\ldots ,0)\}\quad \sum _{j}\alpha _{j}\mathbf {a} _{j}=0\right)\iff \bigwedge _{j=1}^{k}\mathbf {a} _{j}=0.

Identité de Jacobi[modifier | modifier le code]

Structures remarquables[modifier | modifier le code]

Espace quadratique[modifier | modifier le code]

Puisque le produit intérieur de deux vecteurs est un scalaire et qu'il est distributif et symétrique, il constitue une forme quadratique sur ${\mathcal {V}}$ et confère ainsi aux vecteurs de l'algèbre géométrique une structure quadratique naturelle.

Dans le cas défini précédemment comme euclidien, le produit intérieur est en outre défini positif, et satisfait donc aux conditions nécessaires et suffisantes pour définir un produit scalaire, rendant ainsi la structure quadratique euclidienne, d'où l'appellation « cas euclidien ». Dans ce cas, les notions de norme et d'orthogonalité définies précédemment coïncident respectivement avec les notions de norme euclidienne et d'orthogonalité au sens euclidien.

Algèbre extérieure[modifier | modifier le code]

Le produit extérieur fournit (en oubliant le produit géométrique dont il est issu) une définition alternative de l'algèbre extérieure de ${\mathcal {V}}$ ^[9] :

\wedge {\mathcal {V}}={\mathcal {G}}\quad {\rm {car}}\quad {\mathcal {G}}=\bigoplus _{k}{\mathcal {G}}^{k}\quad {\rm {et}}\quad {\mathcal {G}}^{k}=\wedge ^{k}{\mathcal {V}}.

Le vocabulaire de l'algèbre géométrique recoupe donc celui des algèbres extérieures. Par exemple, une lame de grade $k$ est aussi appelée multivecteur de grade $k$ , $k$ -multivecteur ou encore $k$ -vecteur.

Sous-algèbres complexes[modifier | modifier le code]

Le carré de tout bivecteur unitaire $(e 1 e 2)$ construit à partir de deux vecteurs de signatures identiques, est égal à –1 :

\mathbf {e} _{1}^{2}\mathbf {e} _{2}^{2}=1\Rightarrow (\mathbf {e} _{1}\mathbf {e} _{2})^{2}=-1.

Dès lors, la sous-algèbre engendrée par le couple $(1, e 1 e 2)$ est un corps isomorphe au corps des complexes. Cet isomorphisme justifie alors la notation :

i=\mathbf {e} _{1}\mathbf {e} _{2}

de telle sorte qu'on a :

i^{2}=-1.

Ce résultat peut en fait être généralisé à toutes les lames unitaires dont le carré est égal à -1. Elles génèrent chacune avec la lame unitaire de grade nul un corps isomorphe au corps des complexes. C'est par exemple le cas pour le pseudoscalaire unitaire dans le cas euclidien de dimension 3 :

I^{2}=-1.

Une lame unitaire de grade 1, c'est-à-dire un vecteur unitaire, peut aussi engendrer un corps isomorphe au corps des complexes. Il faut et suffit pour cela que sa signature soit négative. C'est notamment le cas lorsque la structure quadratique n'est pas euclidienne, mais Lorentzienne. Par ailleurs, lorsqu'il existe au moins deux vecteurs de signatures différentes, il est possible de construire un bivecteur unitaire $j$ tel que $j 2 = +1$ , et la sous-algèbre qu'il engendre avec l'unité est alors isomorphe au corps des nombres complexes déployés, donnant au sous-espace correspondant une structure géométrique hyperbolique.

Quaternions[modifier | modifier le code]

Dans le cas particulier où $n = 3$ , on peut former trois bivecteurs unitaires : $i=\mathbf {e} _{1}\mathbf {e} _{2},\quad j=\mathbf {e} _{2}\mathbf {e} _{3}\quad {\rm {et}}\quad k=\mathbf {e} _{1}\mathbf {e} _{3}.$

Dans le cas euclidien, on a de plus :

$i^{2}=j^{2}=k^{2}=ijk=-1,$

si bien que la sous-algèbre engendrée par $(1, i, j, k)$ est isomorphe au corps des quaternions.

$i$ , $j$ et $k$ ne sont pas exactement les bivecteurs unitaires naturellement générés par la base orthonormale. En effet, on a bien $i = e 1 e 2$ , $j = e 2 e 3$ , mais par contre $k = - e 3 e 1$ . Dans sa thèse de doctorat^[10], Richard Wareham mentionne cette différence et y voit la cause de certaines erreurs de signe apparaissant parfois avec l'utilisation des quaternions. Ce sujet est aussi abordé par Chris Doran^[11].

Algèbre de Lie[modifier | modifier le code]

${\mathcal {G}}^{2}$ est stable par commutateurs. À ce titre, et compte tenu de l'identité de Jacobi, il forme une algèbre de Lie.

Inversibilité[modifier | modifier le code]

Une algèbre géométrique hérite de sa structure d'anneau unitaire la notion d'inverse : un élément $A$ est dit inversible s'il existe un élément $A -1$ (qui est alors unique) tel que

AA^{-1}=A^{-1}A=1.

Lorsque ${\mathcal {V}}$ est non dégénéré, tout vecteur de ${\mathcal {V}}$ est inversible :

\mathbf {a} ^{-1}={\frac {\mathbf {a} }{\mathbf {a} ^{2}}}.

Toujours dans le cas non dégénéré, les verseurs sont eux aussi inversibles, comme produits d'inversibles. Le calcul de l'inverse d'un verseur passe par celui de sa réversion, c'est-à-dire le verseur qui est le produit extérieur des mêmes vecteurs, mais dans l'ordre inverse.

Règle de De Morgan[modifier | modifier le code]

(A\vee B)^{\sim }={\widetilde {A}}\wedge {\widetilde {B}}.

Identités remarquables[modifier | modifier le code]

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue pour adapter les notations et effectuer les démonstrations !

Les identités remarquables suivantes sont mentionnées dans McDonald 2015. Toutes ne sont pas relevées du fait de notations légèrement différentes.

${\begin{aligned}A\cdot (B\cdot C)&=(A\wedge B)\cdot C\\(\mathbf {a} \wedge \mathbf {b} )\cdot (\mathbf {c} \wedge \mathbf {d} )&=(\mathbf {a} \cdot \mathbf {d} )(\mathbf {b} \cdot \mathbf {c} )-(\mathbf {a} \cdot \mathbf {c} )(\mathbf {b} \cdot \mathbf {d} )\\\mathbf {a} \cdot (\mathbf {bc} )&=(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} -(\mathbf {a} \cdot \mathbf {c} )\mathbf {b} \\\mathbf {a} \cdot (\mathbf {b} \wedge \mathbf {c} )&=(\mathbf {a} \cdot \mathbf {b} )\mathbf {c} -\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )\end{aligned}}$

Lien avec le produit vectoriel[modifier | modifier le code]

Le produit extérieur $a \land b$ n'est ni un scalaire, ni un vecteur : c'est un bivecteur, qui sera identifié plus tard comme le dual du vecteur issu du produit vectoriel. La différence entre les deux opérations étant que le bivecteur fourni par le produit extérieur est intrinsèque au plan des deux vecteurs, tandis que le produit vectoriel est noté comme un pseudovecteur perpendiculaire à ce plan.

Le produit extérieur de deux vecteurs peut être vu comme une aire orientée.

Interprétation géométrique[modifier | modifier le code]

Cette section a besoin d'être recyclée (2 avril 2016).
Une réorganisation et une clarification du contenu sont nécessaires.

Bivecteurs unitaires[modifier | modifier le code]

Un bivecteur unitaire $s$ est le produit géométrique de deux vecteurs orthonormés que l'on peut, sans perdre en généralité, considérer comme les deux premiers vecteurs d'une base orthonormée $(e 1, e 2, ...)$ :

s=\mathbf {e} _{1}\mathbf {e} _{2}

L'orthonormalité de $e 1$ et $e 2$ donne, entre autres :

s=\mathbf {e} _{1}\mathbf {e} _{2}=\mathbf {e} _{1}\wedge \mathbf {e} _{2}=-\mathbf {e} _{2}\wedge \mathbf {e} _{1}=-\mathbf {e} _{2}\mathbf {e} _{1}

Le caractère remarquable de $s$ provient du fait que le produit géométrique par $s$ laisse stable l'espace vectoriel généré par $(e 1, e 2, ...)$ , et défini donc une transformation linéaire (ou plus précisément deux transformations linéaires, selon que la multiplication a lieu à droite ou à gauche), permettant ainsi une interprétation géométrique directe :

${\begin{aligned}(\alpha \mathbf {e} _{1}+\beta \mathbf {e} _{2})s=&(\alpha \mathbf {e} _{1}^{2})\mathbf {e} _{2}&-(\beta \mathbf {e} _{2}^{2})\mathbf {e} _{1}\\s(\alpha \mathbf {e} _{1}+\beta \mathbf {e} _{2})=&(-\alpha \mathbf {e} _{1}^{2})\mathbf {e} _{2}&+(\beta \mathbf {e} _{2}^{2})\mathbf {e} _{1}\end{aligned}}$

Le point important ici étant que $e 21$ et $e 22$ sont scalaires du fait du critère de contraction.

Le carré de $s$ est un scalaire, car

s^{2}=-\mathbf {e} _{1}^{2}\mathbf {e} _{2}^{2}.

Il est négatif si $e 1$ et $e 2$ ont la même signature, et positif dans le cas contraire. Le comportement algébrique (et géométrique dans le plan $(e 1, e 2, ...)$ ) de $s$ est radicalement différent dans les deux cas.

Cas euclidien[modifier | modifier le code]

Lorsque $e 1$ et $e 2$ ont la même signature, on a soit $\mathbf {e} _{1}^{2}=\mathbf {e} _{2}^{2}=+1$ soit $\mathbf {e} _{1}^{2}=\mathbf {e} _{2}^{2}=-1$ . Dans les deux cas le bivecteur $e 1 e 2$ a les mêmes propriétés algébriques et géométriques, mais pour fixer les idées on choisira ici $\mathbf {e} _{1}^{2}=\mathbf {e} _{2}^{2}=+1$ , c'est-à-dire le cas euclidien.

On a alors la propriété importante $s^{2}=-\mathbf {e} _{1}^{2}\mathbf {e} _{2}^{2}=-1$ , c'est-à-dire :

s^{2}=-1.

$s$ engendre alors avec l'unité une sous-algèbre isomorphe au corps des complexes, comme vu plus haut. Ceci suggère d'utiliser dorénavant la lettre $i$ au lieu de $s$ dans cette section.

On aura également les relations suivantes :

{\begin{aligned}i\mathbf {e_{1}} &=-\mathbf {e_{2}} \\i\mathbf {e_{2}} &=\mathbf {e_{1}} \end{aligned}}

{\begin{aligned}\mathbf {e_{1}} i&=\mathbf {e_{2}} \\\mathbf {e_{2}} i&=-\mathbf {e_{1}} \end{aligned}}

C'est-à-dire que la multiplication par $i$ tourne toute combinaison linéaire de $(e 1, e 2, ...)$ d'un quart de tour, dans un sens qui dépend du côté selon lequel est effectuée la multiplication (à gauche ou à droite). On peut s'assurer du fait que la rotation est d'un quart de tour par exemple en remarquant que 4 est le plus petit entier $k$ tel que $i k = 1$ . Il s'avère que cette rotation d'un quart de tour génère un groupe de rotations, comme il est montré ci-après.

Le produit géométrique d'une paire de vecteurs unitaires $\mathbf {a} ,\mathbf {b} \,(|\mathbf {a} |=|\mathbf {b} |=1)\,$ est noté $U$ et est appelé tourneur^[12]:

U=\mathbf {ab}

Le nom tourneur est justifié par le fait que $U$ transforme $a$ et $b$ l'un envers l'autre par rotation:

\mathbf {b} =\mathbf {a} U,\quad \mathbf {a} =U\mathbf {b}

Lorsque $a$ et $b$ sont dans le plan $(e 1, e 2, ...)$ , on peut sans perdre en généralité choisir $e 1 = a$ et trouver un angle $θ$ tel que :

\mathbf {b} =\cos(\theta )\mathbf {e} _{1}+\sin(\theta )\mathbf {e} _{2}

$U$ s'écrit alors :

$U=\mathbf {ab} =\cos(\theta )\mathbf {e} _{1}\mathbf {e} _{1}+\sin(\theta )\mathbf {e} _{1}\mathbf {e} _{2}=\cos(\theta )+\sin(\theta )\mathbf {e} _{1}\mathbf {e} _{2}$

et donc, par association des parties scalaires et bivectorielles de la décomposition canonique:

{\begin{aligned}\mathbf {a} \cdot \mathbf {b} &=\cos(\theta )\\\mathbf {a} \wedge \mathbf {b} &=i\sin(\theta )\end{aligned}}

où $i$ est le bivecteur unitaire :

i=\mathbf {e} _{1}\mathbf {e} _{2}={\frac {\mathbf {a} \wedge \mathbf {b} }{\sin(\theta )}}={\frac {U-\cos(\theta )}{\sin(\theta )}}.

Il est alors possible d'écrire :

$U=U_{\theta }=\mathbf {ab} =\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} =\cos(\theta )+i\sin(\theta )=e^{i\theta },$

c'est-à-dire^[13] :

U_{\theta }=e^{i\theta }.

Lorsqu'on multiplie (par exemple à gauche) ce tourneur par un vecteur $x (ϕ)$ tel que :

$\mathbf {x} (\phi )=\cos(\phi )\mathbf {e} _{1}+\sin(\phi )\mathbf {e} _{2}$

on obtient, par application des identités trigonométriques ainsi que des règles algébriques d'orthonormalité de $e 1$ et $e 2$ :

${\begin{aligned}\mathbf {x} (\phi )U_{\theta }&=\mathbf {x} (\phi )e^{i\theta }\\&=(\cos(\phi )\mathbf {e} _{1}+\sin(\phi )\mathbf {e} _{2})(\cos(\theta )+i\sin(\theta ))\\&=\cos(\phi )\mathbf {e} _{1}\cos(\theta )+\sin(\phi )\mathbf {e} _{2}\cos(\theta )+\cos(\phi )\mathbf {e} _{1}i\sin(\theta )+\sin(\phi )\mathbf {e} _{2}i\sin(\theta )\\&=(\cos(\phi )\cos(\theta )-\sin(\phi )\sin(\theta ))\mathbf {e} _{1}+(\cos(\theta )\sin(\phi )+\cos(\phi )\sin(\theta ))\mathbf {e} _{2}\\&=\cos(\phi +\theta )\mathbf {e} _{1}+\sin(\phi +\theta )\mathbf {e} _{2}\\&=\mathbf {x} (\phi +\theta ).\end{aligned}}$

Le vecteur $x (ϕ)$ a donc bien « tourné » d'un angle $θ$ . Un calcul similaire montrerait qu'une multiplication à droite fait tourner $x (ϕ)$ d'un angle $-θ$ .

En résumé :

{\begin{aligned}\mathbf {x} (\phi )U_{\theta }&=\mathbf {x} (\phi +\theta )\\U_{\theta }\mathbf {x} (\phi )&=\mathbf {x} (\phi -\theta ).\end{aligned}}

Le produit géométrique de deux vecteurs unitaires représente donc bien une rotation.

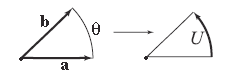
Il y a une analogie entre tourneur et vecteur.

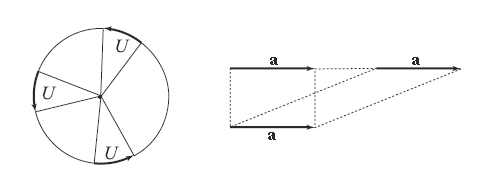
Une composition de rotation s'exprimera par le produit de deux tourneurs :

U_{\theta }U_{\varphi }=U_{\theta +\varphi }

Il est utile d'observer que :

U_{\varphi }\mathbf {x} (\phi )U_{\psi }=U_{\varphi }\mathbf {x} (\phi +\psi )=\mathbf {x} (\phi +\psi -\varphi )

et que donc, pour $ϕ = - θ /2$ et $ψ = θ /2$ :

U_{-{\frac {\theta }{2}}}\mathbf {x} (\phi )U_{\frac {\theta }{2}}=\mathbf {x} (\phi +\theta )

Ceci constitue la formulation dite canonique de la rotation d'angle $θ$ . Cette formulation présente comme avantage d'être extensible aux dimensions supérieures (notamment dans l'espace tridimensionnel).

Espace de Minkowski[modifier | modifier le code]

Lorsque $e 1$ et $e 2$ ont une signature différente (admettons par exemple, pour fixer les idées, que $\mathbf {e} _{1}^{2}=1$ et $\mathbf {e} _{2}^{2}=-1$ ), on a $s^{2}=-\mathbf {e} _{1}^{2}\mathbf {e} _{2}^{2}=1$ , c'est-à-dire :

s^{2}=1

La multiplication par $s$ intervertit $e 1$ et $e 2$ :

\mathbf {e} _{1}s=\mathbf {e} _{1}\mathbf {e} _{1}\mathbf {e} _{2}=\mathbf {e} _{1}^{2}\mathbf {e} _{2}=\mathbf {e} _{2}

\mathbf {e} _{2}s=\mathbf {e} _{2}\mathbf {e} _{1}\mathbf {e} _{2}=-\mathbf {e} _{2}\mathbf {e} _{2}\mathbf {e} _{1}=-\mathbf {e} _{2}^{2}\mathbf {e} _{1}=\mathbf {e} _{1},

c'est-à-dire :

{\begin{aligned}\mathbf {e} _{1}s&=\mathbf {e} _{2}\\\mathbf {e} _{2}s&=\mathbf {e} _{1}\end{aligned}}

{\begin{aligned}s\mathbf {e} _{1}&=-\mathbf {e} _{2}\\s\mathbf {e} _{2}&=-\mathbf {e} _{1}.\end{aligned}}

La multiplication par $s$ agit donc dans le plan $(e 1, e 2, ...)$ comme une réflexion dont l'axe est l'une des bissectrices des droites dirigées par $e 1$ et $e 2$ , le choix de la bissectrice dépendant du côté où s'effectue la multiplication (à droite ou à gauche).

Le fait que $s 2 = 1$ est cohérent avec le caractère involutif des réflexions.

Multiplication par un verseur[modifier | modifier le code]

Sauf mention contraire, on se limitera à partir d'ici au cas euclidien.

Cas général[modifier | modifier le code]

On considère désormais un couple de vecteurs $(a, b)$ non nécessairement unitaires, mais non nuls et non colinéaires. Les résultats précédents peuvent être généralisés en considérant le couple :

(\mathbf {\tilde {a}} ,\mathbf {\tilde {b}} )=({\frac {\mathbf {a} }{|\mathbf {a} |}},{\frac {\mathbf {b} }{|\mathbf {b} |}})

Les vecteurs $\mathbf {\tilde {a}}$ et $\mathbf {\tilde {b}}$ sont, eux, unitaires, et ont les mêmes signatures que $a$ et $b$ . Ils sont aussi séparés par un même angle $θ$ , de telle sorte que le tourneur $\mathbf {\tilde {a}} \mathbf {\tilde {b}}$ s'écrit :

\mathbf {\tilde {a}} \mathbf {\tilde {b}} =e^{i\theta }

où

i={\frac {\mathbf {\tilde {a}} \wedge \mathbf {\tilde {b}} }{\sin(\theta )}}.

Le produit géométrique peut donc s'écrire :

\mathbf {a} \mathbf {b} =|\mathbf {a} ||\mathbf {b} |e^{i\theta }

tandis que le bivecteur unitaire $i$ peut s'écrire :

i={\frac {\mathbf {a} \wedge \mathbf {b} }{|\mathbf {a} ||\mathbf {b} |\sin(\theta )}}.

On a vu précédemment que l'ensemble de multivecteurs engendré — par les combinaisons linéaires et produits géométriques — par 1 et $i$ est un corps isomorphe au corps des nombres complexes. Ceci justifie l'emploi d'un vocabulaire et de notations analogues.

Ainsi, si l'on note $z$ le produit $ab$ , le scalaire

|z|=|\mathbf {a} \mathbf {b} |=|\mathbf {a} ||\mathbf {b} |

est ce qu'on appelle le module de $z$ . Il s'agit d'une notion très différente de la norme (ou grandeur) évoquée plus haut, car cette dernière n'est définie que pour les vecteurs, et $z$ n'est pas un vecteur.

Tout comme un nombre complexe peut être décomposé en une partie réelle et une partie imaginaire, un produit géométrique peut être décomposé en deux parties qui ne sont ni plus ni moins que les produits intérieur et extérieur, qu'on peut aussi appeler symétrique et antisymétrique, ou encore scalaire et bivectoriel.

{\begin{aligned}z&=\mathbf {a} \cdot \mathbf {b} &+&\mathbf {a} \wedge \mathbf {b} \\&=|z|\cos(\theta )&+&|z|i\sin(\theta ).\end{aligned}}

De la même façon, $θ$ peut être appelé argument de $z$ .

$z$ peut être interprété géométriquement comme l'arc orienté d'un cercle de rayon $z$ .

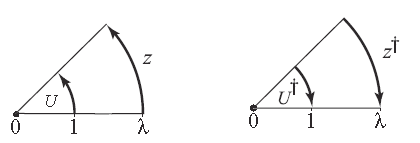
Le conjugué de $z$ est le multivecteur de même partie scalaire mais de composante bivectorielle opposée :

z^{\dagger }=(\mathbf {ab} )^{\dagger }=\mathbf {a} \cdot \mathbf {b} -\mathbf {a} \wedge \mathbf {b} =\mathbf {b} \cdot \mathbf {a} +\mathbf {b} \wedge \mathbf {a} =\mathbf {ba}

Le conjugué d'un produit géométrique apparaît donc comme le produit géométrique effectué en ordre inverse :

(\mathbf {ab} )^{\dagger }=\mathbf {ba} .

Ce fait peut être utilisé pour calculer le module du produit géométrique $z$ .

$|zz^{\dagger }|=|\mathbf {a} \mathbf {b} \mathbf {b} \mathbf {a} |=|\mathbf {a} ^{2}\mathbf {b} ^{2}|=|\mathbf {a} |^{2}|\mathbf {b} |^{2}=|z|^{2}$

autrement dit :

|z|={\sqrt {|zz^{\dagger }|}}.

Les produits géométriques peuvent être utilisés directement sur les vecteurs :

\mathbf {b} =\mathbf {a} ^{-1}z=z^{\dagger }\mathbf {a} ^{-1}

avec l'inverse du vecteur $a$ donné par

\mathbf {a} ^{-1}={\frac {1}{\mathbf {a} }}={\frac {\mathbf {a} }{\mathbf {a} ^{2}}}={\frac {\mathbf {a} }{|\mathbf {a} |^{2}}}.

Ici, le produit géométrique $z$ opère une rotation sur le vecteur $a$ , le met à l'échelle pour donner le vecteur $b$ (c'est une similitude).

Espace euclidien de dimension 3[modifier | modifier le code]

Soit l'espace vectoriel euclidien ${\mathcal {P}}^{3}$ . Par multiplication et addition, les vecteurs engendrent une algèbre géométrique ${\mathcal {G}}_{3}={\mathcal {G}}\left({\mathcal {P}}^{3}\right)$ . En particulier, on peut construire une base pour l'algèbre géométrique à partir de la base orthonormée canonique $\lbrace \mathbf {\sigma _{1}} ,\mathbf {\sigma _{2}} ,\mathbf {\sigma _{3}} \rbrace$ de ${\mathcal {P}}^{3}$ .

À l'aide du produit géométrique, on peut définir l'unité pseudoscalaire (qui représente un volume orienté) :

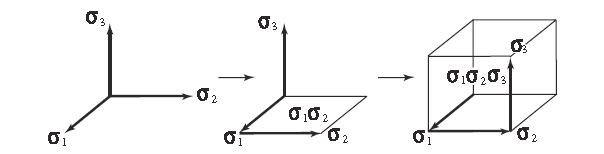
i=\mathbf {\sigma _{1}} \mathbf {\sigma _{2}} \mathbf {\sigma _{3}} .

On a également la base de bivecteurs suivante

\mathbf {\sigma _{1}} \mathbf {\sigma _{2}} =i\mathbf {\sigma _{3}} ,\,\mathbf {\sigma _{2}} \mathbf {\sigma _{3}} =i\mathbf {\sigma _{1}} ,\,\mathbf {\sigma _{3}} \mathbf {\sigma _{1}} =i\mathbf {\sigma _{2}}

Les bivecteurs unités représentent des aires orientées.

Le pseudoscalaire $i$ a des propriétés spéciales qui facilitent le passage entre l'espace vectoriel euclidien et l'algèbre géométrique. On a :

i^{2}=-1

Tout bivecteur $B$ de ${\mathcal {G}}_{3}$ est le dual d'un vecteur $b$ en considérant la relation :

\mathbf {B} =i\mathbf {b} =\mathbf {b} i

Ainsi l'opération de dualité géométrique est simplement exprimée par la multiplication par le pseudoscalaire $i$ . Cela permet d'écrire le produit extérieur sous cette forme :

\mathbf {a} \wedge \mathbf {b} =i\mathbf {a} \times \mathbf {b}

,

$a \times b$ étant le « cross-product anglo-saxon », qui correspond au produit vectoriel dans la littérature scientifique française, lequel produit vectoriel est malencontreusement noté $\land$ comme le produit extérieur. Le produit vectoriel est ainsi implicitement défini comme le dual du produit extérieur. Par conséquent, la décomposition canonique du produit géométrique peut être mise sous la forme :

\mathbf {a} \mathbf {b} =\mathbf {a} \cdot \mathbf {b} +i\mathbf {a} \times \mathbf {b}

C'est grâce à cette définition que l'on pourra faire le lien entre l'algèbre géométrique et l'analyse vectorielle standard.

Les éléments d'une algèbre géométrique sont dénommés des multivecteurs. Les propriétés spéciales du pseudoscalaire $i$ permettent d'écrire tout multivecteur $M$ de ${\mathcal {G}}_{3}$ dans sa forme étendue :

M=\alpha +\mathbf {a} +i\mathbf {b} +i\beta

,

où $α$ et $β$ sont des scalaires et où $a$ et $b$ sont des vecteurs. L'intérêt de cette formulation est qu'elle réduit la multiplication de multivecteurs dans ${\mathcal {G}}_{3}$ à celle des vecteurs. Les quatre termes d'un multivecteur sont linéairement indépendant, ainsi les parties scalaire, vecteur, bivecteur et pseudoscalaire des multivecteurs se combinent séparément lors d'une addition, ce qui n'est pas le cas pour la multiplication.

L'algèbre géométrique ${\mathcal {G}}_{3}$ est un espace linéaire de dimension 1+3+3+1=2³=8.

La forme étendue d'un multivecteur a la structure algébrique formelle d'un « scalaire complexe » $α + i β$ augmenté d'un « vecteur complexe » $a + i b$ , mais toute interprétation physique repose sur la signification géométrique du pseudoscalaire $i$ .

Correspondances[modifier | modifier le code]

Avec les quaternions

Algèbre géométrique	Quaternions	Interprétation
1	1	scalaire
$\sigma _{2}\sigma _{3}$	-i	plan orienté yz
$\sigma _{3}\sigma _{1}$	-j	plan orienté zx
$\sigma _{1}\sigma _{2}$	-k	plan orienté xy

Avec les biquaternions

Algèbre géométrique	Biquaternions	Interprétation
1	1	point défini par son rayon-vecteur
$\sigma _{1}$	i i	droite orientée (vecteur selon l'axe x)
$\sigma _{2}$	i j	droite orientée (vecteur selon l'axe y)
$\sigma _{3}$	i k	droite orientée (vecteur selon l'axe z)
$\sigma _{1}\sigma _{2}$	-k	plan orienté xy (bivecteur)
$\sigma _{2}\sigma _{3}$	-i	plan orienté yz (bivecteur)
$\sigma _{3}\sigma _{1}$	-j	plan orienté zx (bivecteur)
$\sigma _{1}\sigma _{2}\sigma _{3}$	i	volume orienté xyz (trivecteur)

Avec l'algèbre des matrices

L'algèbre géométrique ${\mathcal {G}}_{3}$ est analogue à l'algèbre construite sur des matrices 2 × 2 à coefficients complexes. Cette algèbre se retrouve en mécanique quantique, introduite par Wolfgang Pauli, pour modéliser le spin des particules. La base canonique de cette algèbre est constituée des huit matrices complexes de dimensions 2 × 2 suivantes :

pour les vecteurs, les trois matrices de Pauli :

\sigma _{1}=\sigma _{x}={\begin{pmatrix}0&1\\1&0\end{pmatrix}},\quad \sigma _{2}=\sigma _{y}={\begin{pmatrix}0&-i\\i&0\end{pmatrix}},\quad \sigma _{3}=\sigma _{z}={\begin{pmatrix}1&0\\0&-1\end{pmatrix}}~;

pour les bivecteurs :

\sigma _{1}\sigma _{2}=\sigma _{xy}={\begin{pmatrix}i&0\\0&-i\end{pmatrix}},\quad \sigma _{2}\sigma _{3}=\sigma _{yz}={\begin{pmatrix}0&i\\i&0\end{pmatrix}},\quad \sigma _{3}\sigma _{1}=\sigma _{zx}={\begin{pmatrix}0&1\\-1&0\end{pmatrix}}~;

pour les trivecteurs :

\sigma _{1}\sigma _{2}\sigma _{3}=\sigma _{xyz}={\begin{pmatrix}i&0\\0&i\end{pmatrix}}~;

pour les scalaires :

\sigma _{0}=1={\begin{pmatrix}1&0\\0&1\end{pmatrix}}.

Discussion[modifier | modifier le code]

Le point distinctif de cette formulation est la correspondance naturelle entre les entités et les éléments de l'algèbre associative. Ceci provient du fait que le produit géométrique de deux vecteurs peut être redéfini en termes de leur produit vectoriel et de leur produit scalaire, par

\mathbf {a} \,\mathbf {b} =\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \wedge \mathbf {b} .

On suppose que le corps des scalaires de l'espace vectoriel original ${\mathcal {V}}$ est le corps des réels.

La définition et l'associativité du produit géométrique nécessitent le concept d'inverse d'un vecteur (ou division par un vecteur). Ainsi, on peut facilement établir et résoudre des équations algébriques vectorielles qui autrement seraient encombrantes à manipuler. De plus, on gagne une signification géométrique qui serait difficile à rechercher, par exemple, en utilisant les matrices. Malgré le fait que tous les éléments ne sont pas inversibles, le concept d'inversion peut être étendu aux multivecteurs. L'algèbre géométrique permet que l'on traite des sous-espaces directement, ainsi que leur manipulation. En outre, l'algèbre géométrique est un formalisme sans coordonnées.

Les objets géométriques comme $a \land b$ sont appelés des bivecteurs. Un bivecteur peut être décrit comme un segment plan (un parallélogramme, un cercle, etc.) doté d'une orientation. Un bivecteur représente tous les segments planaires avec la même grandeur et direction, quel que soit l'endroit où ils se trouvent dans l'espace qui les contient. Néanmoins, une fois que soit le vecteur $a$ ou $b$ est signifié à partir d'un certain point préféré (e.g. dans les problèmes de physique), le plan orienté $B = a \land b$ est déterminé sans ambiguïté.

Comme exemple significatif, bien que simple, on peut considérer le rayon-vecteur $v$ différent de zéro, d'un point d'un espace euclidien affine usuel, $\mathbb {R} ^{3}$ (rappelons que le rayon-vecteur d'un point affine est le vecteur qui part de l'origine et aboutit à ce point). L'ensemble de tous les points de rayons-vecteurs $x$ tels que $x \land v = B$ , $B$ désignant un bivecteur donné contenant $v$ , détermine une droite $l$ parallèle à $v$ . Puisque $B$ est une aire orientée, $l$ est uniquement déterminé en conservant l'origine choisie. L'ensemble de tous les points de rayons-vecteurs $x$ tels que $x . v = s$ , $s$ désignant un scalaire (réel) donné, détermine un plan P orthogonal à $v$ . De nouveau, P est uniquement déterminé en conservant l'origine choisie. Les deux morceaux d'information, $B$ et $s$ , peuvent être établis indépendamment l'un de l'autre. Maintenant, quel est le rayon-vecteur $y$ qui satisfait le système ${y \land v = B, y . v = s}$ ? Géométriquement, la réponse est claire : c'est le rayon-vecteur de l'intersection de $l$ et P. Par l'algèbre géométrique, même la réponse algébrique est simple :

\mathbf {y} \mathbf {v} =s+B\Rightarrow \mathbf {y} =(s+B)/\mathbf {v} =(s+B)\mathbf {v} ^{-1}

où l'inverse d'un vecteur différent de zéro est exprimé par $z -1 = z / z • z$ .

Note : La division par un vecteur transforme le multivecteur $s + B$ en une somme de deux vecteurs. De plus, la structure de la solution ne dépend pas de l'origine choisie.

Tel qu'il est défini, le produit externe (ou produit extérieur, ou produit vectoriel) $\land$ engendre l'algèbre graduée (algèbre extérieure de Hermann Grassmann) $\wedge ^{n}{\mathcal {V}}_{n}$ des multivecteurs. Un multivecteur est ainsi une somme directe d'éléments de degré k (k-vecteurs), où k va de 0 (scalaires) à n, la dimension de l'espace vectoriel original ${\mathcal {V}}$ . Les multivecteurs sont représentés ici par les majuscules grasses. Note : Les scalaires et les vecteurs deviennent des cas particuliers de multivecteurs (« 0-vecteurs » et « 1-vecteurs », respectivement).

La règle de contraction[modifier | modifier le code]

La connexion entre les algèbres de Clifford et les formes quadratiques provient de la propriété (ou règle) de contraction. Cette règle donne aussi à l'espace une métrique définie par le produit interne naturellement dérivé. Également, dans l'algèbre géométrique dans toute sa généralité, il n'existe pas une quelconque restriction sur la valeur du scalaire, il peut être négatif, même zéro (dans ce cas, la possibilité d'un produit interne est éliminée si vous demandez $\langle x,x\rangle \geq 0$ ).

La règle de contraction peut être mise sous la forme :

Q(\mathbf {a} )=\mathbf {a} ^{2}=\varepsilon _{a}{\Vert \mathbf {a} \Vert }^{2}

où $| a |$ est le module du vecteur $a$ et $\varepsilon _{a}=0,\,\pm 1$ est appelé la signature du vecteur $a$ . Ceci est particulièrement utile dans la construction de l'espace de Minkowski (l'espace-temps de la relativité) via $\mathbb {R} _{1,3}\,$ . Dans ce contexte, les vecteurs nuls sont appelés vecteurs de lumière, les vecteurs à signature négative sont appelés vecteurs d'espace et les vecteurs à signature positive sont appelés vecteurs de temps (ces deux dernières dénominations sont échangées lorsqu'on utilise $\mathbb {R} _{3,1}$ à la place de $\mathbb {R} _{1,3}\,$ ).

Produits intérieur et extérieur[modifier | modifier le code]

Le produit scalaire usuel et le produit vectoriel de l'algèbre vectorielle traditionnelle (sur $\mathbb {R} ^{3}\,$ ) trouvent leurs places dans l'algèbre géométrique ${\mathcal {G}}_{3}\,$ comme le produit interne

\mathbf {a} \cdot \mathbf {b} ={\frac {1}{2}}(\mathbf {a} \mathbf {b} +\mathbf {b} \mathbf {a} )

(qui est symétrique) et le produit externe

\mathbf {a} \wedge \mathbf {b} ={\frac {1}{2}}(\mathbf {a} \mathbf {b} -\mathbf {b} \mathbf {a} )

avec

\mathbf {a} \times \mathbf {b} =-i(\mathbf {a} \wedge \mathbf {b} )

(qui est antisymétrique). La distinction entre vecteurs axiaux et polaires, obscure en algèbre vectorielle, est naturelle en algèbre géométrique, où elle s'exprime comme la distinction entre vecteurs et bivecteurs (éléments de grade deux). Le $i$ ici est l'unité pseudoscalaire du 3-espace euclidien, qui établit une dualité entre les vecteurs et les bivecteurs, et est nommé ainsi à cause de la propriété prévue $i 2 = -1$ .

Alors que le produit vectoriel peut seulement être défini dans un espace à trois dimensions, les produits interne et externe peuvent être généralisés à n'importe quelle dimension.

Soient $\mathbf {a} ,\,\mathbf {A} _{\langle k\rangle }$ un vecteur et un multivecteur homogène de grade k. Leur produit interne est alors : $\mathbf {a} \cdot \mathbf {A} _{\langle k\rangle }={1 \over 2}\,\left(\mathbf {a} \,\mathbf {A} _{\langle k\rangle }+(-1)^{k+1}\,\mathbf {A} _{\langle k\rangle }\,\mathbf {a} \right)=(-1)^{k+1}\mathbf {A} _{\langle k\rangle }\cdot \mathbf {a}$ et leur produit externe est

\mathbf {a} \wedge \mathbf {A} _{\langle k\rangle }={1 \over 2}\,\left(\mathbf {a} \,\mathbf {A} _{\langle k\rangle }-(-1)^{k+1}\,\mathbf {A} _{\langle k\rangle }\,\mathbf {a} \right)=(-1)^{k}\mathbf {A} _{\langle k\rangle }\wedge \mathbf {a} .

Algèbre géométrique conforme[modifier | modifier le code]

Article détaillé : Algèbre géométrique conforme.

Un espace vectoriel, même muni d'un produit scalaire, n'est pas, à lui seul, approprié pour modéliser l'espace usuel, c'est-à-dire l'espace euclidien. En effet, il faut pouvoir distinguer les concepts de points et de vecteurs. Pour cela, plusieurs modèles existent, les plus notables étant l'espace affine et la géométrie projective.

Tandis que la géométrie projective ajoute une dimension supplémentaire, faisant de l'espace usuel un hyperplan, l'algèbre géométrique conforme est un modèle de l'espace euclidien basé sur l'algèbre géométrique qui ajoute non pas une mais deux dimensions supplémentaires. Ces deux dimensions ayant la structure d'un espace de Minkowski, l'espace usuel devient alors une horosphère.

Applications[modifier | modifier le code]

Relativité restreinte et électromagnétisme[modifier | modifier le code]

Un exemple utile est $\mathbb {R} _{3,1}$ , et la façon dont il engendre ${\mathcal {G}}_{3,1}$ , un exemple d'algèbre géométrique qu'Hestenes appelle algèbre de l'espace-temps^[14]. Cette algèbre est dotée d'une base de vecteurs le plus souvent notés $(\mathbf {\gamma } _{0},\mathbf {\gamma } _{1},\mathbf {\gamma } _{2},\mathbf {\gamma } _{3})$ telle que^[15] :

\mathbf {\gamma } _{0}^{2}=-1,\qquad \mathbf {\gamma } _{1}^{2}=\mathbf {\gamma } _{2}^{2}=\mathbf {\gamma } _{3}^{2}=+1

$(\mathbf {\gamma } _{1},\mathbf {\gamma } _{2},\mathbf {\gamma } _{3})$ constitue une base orthonormée de l'espace euclidien usuel. $\mathbf {\gamma } _{0}$ est quant à lui le vecteur séparant deux événements d'une unité de temps.

Le champ électromagnétique, dans ce contexte, s'avère être un champ bivectoriel pour lequel les champs électriques et magnétiques caractérisent les parties respectivement spatio-temporelles (c'est-à-dire contenant la direction temporelle) et purement spatiales (bivecteurs dirigés par deux directions de l'espace usuel) :

F=(\mathbf {E} +i\mathbf {B} )\mathbf {\gamma } _{0}

ou, de façon plus détaillée :

{\begin{aligned}F&=(\mathbf {E} +\mathbf {\gamma } _{0}\mathbf {\gamma } _{1}\mathbf {\gamma } _{2}\mathbf {\gamma } _{3}\mathbf {B} )\mathbf {\gamma } _{0}\\&=\mathbf {E} \mathbf {\gamma } _{0}-\mathbf {B} \mathbf {\gamma } _{1}\mathbf {\gamma } _{2}\mathbf {\gamma } _{3}\\&=E^{k}\mathbf {\gamma } _{k}\mathbf {\gamma } _{0}-B^{k}\mathbf {\gamma } _{k}\mathbf {\gamma } _{1}\mathbf {\gamma } _{2}\mathbf {\gamma } _{3}\\&=E^{k}\mathbf {\gamma } _{k}\mathbf {\gamma } _{0}-(B^{1}\mathbf {\gamma } _{2}\mathbf {\gamma } _{3}+B^{2}\mathbf {\gamma } _{3}\mathbf {\gamma } _{1}+B^{3}\mathbf {\gamma } _{1}\mathbf {\gamma } _{2}).\end{aligned}}

On peut alors montrer que les équations de Maxwell traduisent le fait que le quadrivecteur courant $J=\rho \mathbf {\gamma } _{0}+\mathbf {j}$ dérive de ce champ bivectoriel :

\nabla F=J

$\nabla$ désigne ici le gradient au sens de l’algèbre géométrique, c'est-à-dire tel que défini plus haut : $\nabla =\mathbf {\gamma } ^{\mu }\partial _{\mu }$ . L'expression détaillée de cet opérateur requiert le calcul de $\mathbf {\gamma } ^{0}$ . Comme par définition $\mathbf {\gamma } ^{0}\cdot \mathbf {\gamma } _{0}=1$ , on a $\mathbf {\gamma } ^{0}=-\mathbf {\gamma } _{0}$ , de telle sorte que $\nabla$ s'écrit :

\nabla =-\mathbf {\gamma } _{0}\partial _{0}+\mathbf {\gamma } _{1}\partial _{1}+\mathbf {\gamma } _{2}\partial _{2}+\mathbf {\gamma } _{3}\partial _{3}.

La force de Lorentz s'écrit quant à elle $q\mathbf {u} \cdot F$ , où $q$ et $\mathbf {u}$ sont la charge électromagnétique et la quadrivitesse, de telle sorte que l'équation du mouvement s'écrit, en considérant la quadri-impulsion $\mathbf {p}$ :

{\frac {d}{d\tau }}\mathbf {p} =q\mathbf {u} \cdot F.

Les accélérations dans cet espace métrique lorentzien ont la même expression $e^{\mathbf {\beta } }$ que la rotation dans l'espace euclidien, où $\mathbf {\beta }$ est bien sûr le bivecteur engendré par le temps et les directions d'espace impliquées, considérant dans le cas euclidien que c'est le bivecteur engendré par les deux directions d'espace, renforçant l'« analogie » de la quasi-identité.

Infographie[modifier | modifier le code]

En 2014, il existe au moins une compagnie utilisant l'algèbre géométrique en infographie, et plus particulièrement dans l'industrie du jeu vidéo. Il s'agit de Geomerics (en), fondée en 2005 notamment par Chris J. L. Doran (en), docteur en physique. Doran a déclaré avoir fondé Geomerics précisément dans le but de trouver d'autres manières d'attirer l'attention de la communauté scientifique vers les méthodes de l'algèbre géométrique.

En mars 2014, la société Unity Technologies a entamé une collaboration avec Geomerics pour l'intégration de leur moteur de rendu d'illumination globale en temps réel au sein de la cinquième version du moteur Unity.

Bibliographie[modifier | modifier le code]

(en) David Hestenes (2003), "Oersted Medal Lecture 2002: Reforming the Mathematical Language of Physics" (PDF), Am. J. Phys., 71 (2)
(en) David Hestenes (2003), "Spacetime Physics with Geometric Algebra" (PDF), Am. J. Phys., 71 (6)
(en) David Hestenes (1999), "New Foundations for Classical Mechanics", Springer Verlag, (ISBN 978-0-7923-5302-7)
(en) Chris Doran, Anthony Lasenby (2003), "Geometric Algebra for Physicist", Cambridge University Press, (ISBN 978-0-521-71595-9)
(en) Leo Dorst, Daniel Fontijne, Stephen Mann (2007), "Geometric Algebra for Computer Science", Elsevier/Morgan Kaufman, (ISBN 978-0-12-369465-2)
Gaston Casanova (1976), "L'algèbre vectorielle", Presses Universitaires de France, (ISBN 978-2130343059)
Georges Pagis (2018), "G.A. Maths Physique pour demain", (ISBN 978-1980691389)

Références[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Geometric algebra » (voir la liste des auteurs).
(en) W. E. Baylis (éd.), Clifford (Geometric) Algebra with Applications to Physics, Mathematics, and Engineering, Boston, Birkhäuser, 1996
(en) Chris Doran, Geometric Algebra and its Application to Mathematical Physics, PhD, Sidney Sussex College, 1994
(en) David Hestenes et Garret Sobczyk, Clifford Algebra to Geometric Calculus: A Unified Language for Mathematics and Physics, Springer, 1984 (DOI 10.1007/978-94-009-6292-7)
(en) David Hestenes, « A unified language for mathematics and physics », dans J. S. R. Chisholm et A. K. Common, Clifford Algebras and Their Applications in Mathematical Physics, Reidel, 1986 (DOI 10.1007/978-94-009-4728-3_1, lire en ligne), p. 1-23
(en) David Hestenes, Hongbo Li et Alyn Rockwood, « New Algebraic Tools for Classical Geometry », dans Gerald Sommer, Geometric Computing with Clifford Algebras, Springer, 2001 (DOI 10.1007/978-3-662-04621-0_1, lire en ligne), p. 3-26
(en) Alan McDonald, « A Survey of Geometric Algebra and Geometric Calculus », sur Luther College (Iowa) (en), 2015
(en) Geometric Algebra for Electrical and Electronic Engineers, IEEE digital library
(en) Electromagnetism using Geometric Algebra versus Components

Notes[modifier | modifier le code]

↑ ^{a et b} Autrement dit : tout élément de l'algèbre géométrique est une somme de produits d'éléments du sous-espace vectoriel.
↑ ^{a et b} Hestenes 1986, p. 5 : Directed numbers are defined implicitly by specifying rules for adding and multiplying vectors. Specifically, we assume that the vectors generate an associative algebra in which the square of every vector is a scalar. (« Les nombres dirigés sont définis implicitement en spécifiant les règles d'addition et de multiplication de vecteurs. Plus précisément, nous supposons que les vecteurs engendrent une algèbre associative dans laquelle le carré d'un vecteur est un scalaire. »)
↑ Comme dans toute algèbre unitaire, $\mathbb {K}$ est identifié à $\mathbb {K} 1$ où $1$ est l'élément neutre pour la multiplication bilinéaire.
↑ Hestenes 1986, p. 7 : I am of half a mind to outlaw the Complex Clifford Algebras altogether, because the imaginary scalars do not have a natural geometric interpretation, and their algebraic features exist already in the real Clifford Algebras. However, there is already a considerable literature on complex Clifford Algebras, and they do have some formal advantages. (« Je suis tenté d'interdire complètement l'utilisation d'algèbres de Clifford complexes, parce que des scalaires imaginaires n'ont pas d'interprétation géométrique naturelle, et que leur propriétés algébriques existent déjà dans les algèbres de Clifford réelles. Cependant, il existe déjà une littérature considérable sur les algèbres de Clifford complexes, et elles présentent bel et bien certains avantages formels. »)
↑ On suppose, ici et dans tout le reste de l'article, que la caractéristique de $\mathbb {K}$ est différente de 2, c'est-à-dire que 2 est non nul et donc inversible.
↑ La notation $e_{J}$ , c'est-à-dire utilisant une lettre majuscule en indice, est ici empruntée à McDonald 2015. On a choisi cependant de ne pas utiliser de gras pour le symbole $e$ lorsqu'il est utilisé ainsi, puisqu'il ne désigne pas un vecteur, mais un produit géométrique de vecteurs.
↑ L'existence de pseudoscalaires unitaires n'est pas assurée. Dans le cas contraire, ${\mathcal {V}}^{n}$ est dit dégénéré. Dans cet article et sauf mention contraire, on se place dans le cas non dégénéré.
↑ On a choisi de ne pas utiliser ici le symbole $\parallel$ pour exprimer la colinéarité. En effet, $\parallel$ est utilisé pour exprimer le parallélisme, notion utilisée essentiellement en géométrie affine et qui, selon Euclide, désigne deux droites coplanaires qui ne se rencontrent pas lorsqu'elles sont prolongées de part et d'autre à l'infini. On a préféré le symbole $\propto$ exprimant la proportionnalité.
↑ Hestenes 1986, p. 7, ne craint pas de révéler que les définitions classiques des algèbres tensorielle et extérieure de ${\mathcal {V}}$ et des (multiples) algèbres de Clifford sur ${\mathcal {V}}$ sont pour lui hermétiques : « Clifford algebras are sometimes defined as certain ideals in tensor algebras [sic]. There is nothing logically wrong with this, but I submit that it is better mathematical design to reverse the process and introduce tensor as multilinear functions defined on Clifford algebras [re-sic]. » (« Les algèbres de Clifford sont parfois définies comme étant certains idéaux d'algèbres tensorielles. Il n'y a là rien de logiquement faux, mais je propose qu'une meilleure conception mathématique consiste à inverser le processus et introduire les tenseurs comme fonctions multinéaires définies sur les algèbres de Clifford. »
↑ (en) Computer Graphics Using Conformal Geometric Algebra, Richard J. Wareham, thèse de doctorat, p. 26.
↑ Geometric Algebra for physicists, Chris Doran, section 2.4.2 "The bivector algebra"
↑ Le terme « tourneur » est ici choisi pour traduire le terme anglais rotor. Une alternative est « rotateur ».
↑ L'exponentielle est ici à comprendre au sens algébrique, c'est-à-dire que $e^{i\theta }=\sum _{n\geq 0}{\frac {(i\theta )^{n}}{n!}}$ .
↑ Space-time algebra. Voir l'article espace-temps (structure algébrique).
↑ La convention
$\mathbf {\gamma } _{0}^{2}=+1,\qquad \mathbf {\gamma } _{1}^{2}=\mathbf {\gamma } _{2}^{2}=\mathbf {\gamma } _{3}^{2}=-1$
est aussi très souvent utilisée.

Portail des mathématiques

[Somme_de_produits-1] {a et b} Autrement dit : tout élément de l'algèbre géométrique est une somme de produits d'éléments du sous-espace vectoriel.

[Hestenes_1986_p5-2] {a et b} Hestenes 1986, p. 5 : Directed numbers are defined implicitly by specifying rules for adding and multiplying vectors. Specifically, we assume that the vectors generate an associative algebra in which the square of every vector is a scalar. (« Les nombres dirigés sont définis implicitement en spécifiant les règles d'addition et de multiplication de vecteurs. Plus précisément, nous supposons que les vecteurs engendrent une algèbre associative dans laquelle le carré d'un vecteur est un scalaire. »)

[3] Comme dans toute algèbre unitaire, $\mathbb {K}$ est identifié à $\mathbb {K} 1$ où $1$ est l'élément neutre pour la multiplication bilinéaire.

[4] Hestenes 1986, p. 7 : I am of half a mind to outlaw the Complex Clifford Algebras altogether, because the imaginary scalars do not have a natural geometric interpretation, and their algebraic features exist already in the real Clifford Algebras. However, there is already a considerable literature on complex Clifford Algebras, and they do have some formal advantages. (« Je suis tenté d'interdire complètement l'utilisation d'algèbres de Clifford complexes, parce que des scalaires imaginaires n'ont pas d'interprétation géométrique naturelle, et que leur propriétés algébriques existent déjà dans les algèbres de Clifford réelles. Cependant, il existe déjà une littérature considérable sur les algèbres de Clifford complexes, et elles présentent bel et bien certains avantages formels. »)

[Caractéristique-5] On suppose, ici et dans tout le reste de l'article, que la caractéristique de $\mathbb {K}$ est différente de 2, c'est-à-dire que 2 est non nul et donc inversible.

[6] La notation $e_{J}$ , c'est-à-dire utilisant une lettre majuscule en indice, est ici empruntée à McDonald 2015. On a choisi cependant de ne pas utiliser de gras pour le symbole $e$ lorsqu'il est utilisé ainsi, puisqu'il ne désigne pas un vecteur, mais un produit géométrique de vecteurs.

[7] L'existence de pseudoscalaires unitaires n'est pas assurée. Dans le cas contraire, ${\mathcal {V}}^{n}$ est dit dégénéré. Dans cet article et sauf mention contraire, on se place dans le cas non dégénéré.

[8] On a choisi de ne pas utiliser ici le symbole $\parallel$ pour exprimer la colinéarité. En effet, $\parallel$ est utilisé pour exprimer le parallélisme, notion utilisée essentiellement en géométrie affine et qui, selon Euclide, désigne deux droites coplanaires qui ne se rencontrent pas lorsqu'elles sont prolongées de part et d'autre à l'infini. On a préféré le symbole $\propto$ exprimant la proportionnalité.

[9] Hestenes 1986, p. 7, ne craint pas de révéler que les définitions classiques des algèbres tensorielle et extérieure de ${\mathcal {V}}$ et des (multiples) algèbres de Clifford sur ${\mathcal {V}}$ sont pour lui hermétiques : « Clifford algebras are sometimes defined as certain ideals in tensor algebras [sic]. There is nothing logically wrong with this, but I submit that it is better mathematical design to reverse the process and introduce tensor as multilinear functions defined on Clifford algebras [re-sic]. » (« Les algèbres de Clifford sont parfois définies comme étant certains idéaux d'algèbres tensorielles. Il n'y a là rien de logiquement faux, mais je propose qu'une meilleure conception mathématique consiste à inverser le processus et introduire les tenseurs comme fonctions multinéaires définies sur les algèbres de Clifford. »

[10] (en) Computer Graphics Using Conformal Geometric Algebra, Richard J. Wareham, thèse de doctorat, p. 26.

[11] Geometric Algebra for physicists, Chris Doran, section 2.4.2 "The bivector algebra"

[12] Le terme « tourneur » est ici choisi pour traduire le terme anglais rotor. Une alternative est « rotateur ».

[13] L'exponentielle est ici à comprendre au sens algébrique, c'est-à-dire que $e^{i\theta }=\sum _{n\geq 0}{\frac {(i\theta )^{n}}{n!}}$ .

[14] Space-time algebra. Voir l'article espace-temps (structure algébrique).

[15] La convention
$\mathbf {\gamma } _{0}^{2}=+1,\qquad \mathbf {\gamma } _{1}^{2}=\mathbf {\gamma } _{2}^{2}=\mathbf {\gamma } _{3}^{2}=-1$
est aussi très souvent utilisée.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]