Théorème porte-manteau

En mathématiques, le théorème porte-manteau, théorème de Portmanteau ou de Portemanteau est un théorème de probabilité qui fournit une liste de caractérisations de la convergence en loi d'une suite de variables aléatoires.

Convergence en loi

Soit X une variable aléatoire et soit $\left(X_{n}\right)_{n\geq 1}\$ une suite de variables aléatoires, toutes à valeurs dans le même espace métrique (E,d).

Définition — On dit que la suite $\left(X_{n}\right)_{n\geq 1}\$ converge en loi vers X si, pour toute fonction $\varphi \$ continue bornée sur E,

$\lim _{n}\mathbb {E} \left[\varphi (X_{n})\right]\ =\ \mathbb {E} \left[\varphi (X)\right].$

La convergence en loi est souvent notée en ajoutant la lettre ${\mathcal {L}}$ au-dessus de la flèche de convergence:

$X_{n}{\xrightarrow {\mathcal {L}}}X.$

Énoncé

Théorème porte-manteau — Les cinq assertions suivantes sont équivalentes :

1. X_n converge en loi vers X ;
2. pour toute fonction $\varphi$ bornée et uniformément continue sur E,$\lim _{n}\mathbb {E} \left[\varphi (X_{n})\right]\ =\ \mathbb {E} \left[\varphi (X)\right]$ ;
3. pour tout fermé F de E,$\limsup _{n}\mathbb {P} \left(X_{n}\in F\right)\ \leq \ \mathbb {P} \left(X\in F\right)$ ;
4. pour tout ouvert O de E,$\liminf _{n}\mathbb {P} \left(X_{n}\in O\right)\ \geq \ \mathbb {P} \left(X\in O\right)$ ;
5. pour tout borélien A de E tel que $\mathbb {P} \left(X\in \partial A\right)=0$,$\lim _{n}\mathbb {P} \left(X_{n}\in A\right)\ =\ \mathbb {P} \left(X\in A\right)$.

Ici, $\partial A$ désigne la frontière, ou le bord de A.

Conséquences

Pour des variables réelles

D'un point de vue pratique, les propriétés 2 à 5 sont rarement utilisées pour démontrer la convergence en loi, mais la propriété 5 est certainement une conséquence importante de la convergence en loi. D'une part, la propriété 5 préfigure le théorème de l'application continue (en) ; par ailleurs la propriété 5 possède un cas particulier d'usage fréquent, dans le cas où E est la droite réelle :

Proposition — Si X_n converge en loi vers X, alors, dès que la fonction de répartition F de X est continue en x, on a :

$\lim _{n}\ F_{n}(x)\ =\ F(x)$,

où F_n désigne la fonction de répartition de X_n .

Démonstration

Par définition d'une fonction de répartition, la propriété

$\lim _{n}\ F_{n}(x)\ =\ F(x)$,

s'écrit sous la forme :

$\lim _{n}\mathbb {P} \left(X_{n}\in A_{x}\right)\ =\ \mathbb {P} \left(X\in A_{x}\right)$,

pour peu qu'on choisisse

$A_{x}\ =\ ]-\infty ,x]$.

Par ailleurs

$\partial A_{x}\ =\ \{x\}$.

Donc,

$\mathbb {P} \left(X\in \partial A_{x}\right)\ =\ \mathbb {P} \left(X=x\right)\ =\ \ F(x)-F(x_{-})$,

qui est nul si et seulement si F est continue à gauche en x, i.e. si et seulement si F est continue en x (en effet, une fonction de répartition est partout continue à droite).

Cette proposition est en fait une équivalence^[pas clair], et sert souvent, dans le cas des variables aléatoires réelles, de définition de la convergence en loi. En effet, d'un point de vue pédagogique, elle permet d'utiliser efficacement cette notion sans pour autant avoir eu à construire préalablement la théorie de la mesure.

Pour des variables discrètes

Dans le cas de variables aléatoires à valeurs dans un ensemble dénombrable, muni de la topologie discrète, le théorème porte-manteau donne un critère très simple de convergence en loi.

Proposition — Soient $(X_{n})_{n}$ et $X$ des variables aléatoires à valeurs dans un ensemble dénombrable $E$. alors $(X_{n})_{n}$ converge en loi vers $X$ si et seulement si :

$\forall x\in E,\qquad \mathbb {P} (X_{n}=x)~{\xrightarrow[{n\to \infty }]{}}~\mathbb {P} (X=x)$.

Démonstration

On remarque que, pour la topologie discrète, toute partie de $E$ est ouverte et fermée. Par conséquent la frontière de n'importe quelle partie est toujours vide. Ainsi, si l'on a la convergence en loi, on en déduit par le critère 5 du théorème porte-manteau que

$\forall x\in E,\qquad \mathbb {P} (X_{n}=x)~{\xrightarrow[{n\to \infty }]{}}~\mathbb {P} (X=x)$.

Réciproquement, supposons que la limite ci-dessus est valable et fixons $A\subset E$. Alors par le lemme de Fatou

$\liminf _{n}\mathbb {P} (X_{n}\in A)=\liminf _{n}\sum _{x\in A}\mathbb {P} (X_{n}=x)\geq \sum _{x\in A}\liminf _{n}\mathbb {P} (X_{n}=x)=\sum _{x\in A}\mathbb {P} (X=x)=\mathbb {P} (X\in A)$.

Ainsi la convergence en loi est garantie par le critère 4 du théorème porte-manteau.

Démonstration du théorème porte-manteau

Cette démonstration est adaptée de Billingsley 1999, p. 16-17.

1 entraîne 2

Si

$\lim _{n}\mathbb {E} \left[\varphi (X_{n})\right]\ =\ \mathbb {E} \left[\varphi (X)\right]$

est vrai pour toute fonction $\varphi$ bornée et continue sur E, alors cela est vrai en particulier pour toute fonction $\varphi$ bornée et uniformément continue sur E.

2 entraîne 3

Soit F un fermé de E. Pour tout $k\geq 1$, on note

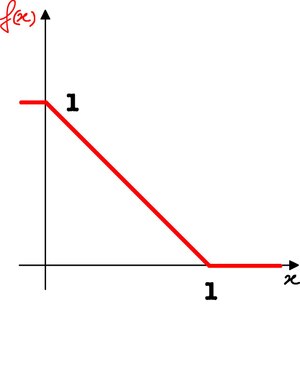
Représentation graphique de l'application $f$.

$F_{k}\ :=\ \left\{x\in E\mid d(x,F)\leq {\tfrac {1}{k}}\right\}$.

De plus, pour tout $x\in E$ et $k>0$, on pose

$\varphi _{k}(x)\ :=\ f\left(k\,d(x,F)\right)=\ {\begin{cases}1-k\,d(x,F)&{\textrm {si}}\ x\in F_{k}\\0&{\textrm {si}}\ x\notin F_{k}\end{cases}}$

où $f$ est définie par la figure ci-contre. Ainsi,

$1_{F}\ \leq \ \varphi _{k}\ \leq \ 1_{F_{k}}$.

Puisque $1_{F}\ \leq \ \varphi _{k}$, on a

$\limsup _{n}\mathbb {P} \left(X_{n}\in F\right)\leq \ \limsup _{n}\mathbb {E} \left[\varphi _{k}(X_{n})\right]$.

Comme les fonctions $f$ et $x\mapsto d(x,F)$ sont 1-lipschitziennes, $\varphi _{k}$ est uniformément continue, et d'après l'hypothèse 2

$\limsup _{n}\mathbb {E} \left[\varphi _{k}(X_{n})\right]\ =\ \lim _{n}\mathbb {E} \left[\varphi _{k}(X_{n})\right]\ =\ \mathbb {E} \left[\varphi _{k}(X)\right]$.

De $\varphi _{k}\ \leq \ 1_{F_{k}}\$, on déduit que

$\mathbb {E} \left[\varphi _{k}(X)\right]\leq \mathbb {P} \left(X\in F_{k}\right)$.

Par conséquent, pour tout $k\geq 1$,

$\limsup _{n}\mathbb {P} \left(X_{n}\in F\right)\leq \ \mathbb {P} \left(X\in F_{k}\right)$.

Enfin, comme $(F_{k})_{k}$ est décroissante et comme $\bigcap _{k\geq 1}F_{k}={\overline {F}}=F$, on a

$\inf _{k}\mathbb {P} \left(X\in F_{k}\right)\ =\ \lim _{k}\mathbb {P} \left(X\in F_{k}\right)\ =\ \mathbb {P} \left(X\in F\right)$,

d'où le résultat.

3 et 4 sont équivalents

Supposons le point 3 vrai, et considérons un ouvert O de E. Alors O^c est un fermé et on a, en vertu, entre autres, du point 3 :

${\begin{aligned}\liminf _{n}\mathbb {P} \left(X_{n}\in {\mathcal {O}}\right)&=\liminf _{n}\left(1-\mathbb {P} \left(X_{n}\in {\mathcal {O}}^{c}\right)\right)\\&=1-\limsup _{n}\mathbb {P} \left(X_{n}\in {\mathcal {O}}^{c}\right)\\&\geq \ 1-\mathbb {P} \left(X\in {\mathcal {O}}^{c}\right)\\&=\mathbb {P} \left(X\in {\mathcal {O}}\right).\end{aligned}}$

La démonstration de « 4 implique 3 » est identique.

3 et 4 entraînent 5

Soit A un borélien de E tel que

$\mathbb {P} \left(X\in \partial A\right)=0$.

Comme

${\stackrel {\ \circ }{A}}\subset A\subset {\overline {A}}={\stackrel {\ \circ }{A}}\cup \partial A$,

on en déduit que

$\mathbb {P} \left(X\in {\overline {A}}\right)\ =\ \mathbb {P} \left(X\in A\right)\ =\ \mathbb {P} \left(X\in {\stackrel {\ \circ }{A}}\right)$.

Or, d'après le point 3

$\limsup _{n}\mathbb {P} \left(X_{n}\in A\right)\leq \limsup _{n}\mathbb {P} \left(X_{n}\in {\overline {A}}\right)\leq \mathbb {P} \left(X\in {\overline {A}}\right)$

et d'après le point 4

$\liminf _{n}\mathbb {P} \left(X_{n}\in A\right)\geq \liminf _{n}\mathbb {P} \left(X_{n}\in {\stackrel {\ \circ }{A}}\right)\geq \mathbb {P} \left(X\in {\stackrel {\ \circ }{A}}\right)$.

Finalement,

$\lim _{n}\mathbb {P} \left(X_{n}\in A\right)=\mathbb {P} \left(X\in A\right)$.

5 entraîne 1

Commençons par traiter le cas où $\psi$ est une fonction continue et bornée, telle que $0<\psi <1$. Alors :

• comme $0<\psi <1$,$\mathbb {E} \left[\psi (X)\right]=\int _{0}^{1}\mathbb {P} \left[\psi (X)>x\right]\,\mathrm {d} x$ et de même pour les $X_{n}$ ;
• comme $\psi$ est continue, $\partial \psi ^{-1}(\left]x,+\infty \right[)\subset \psi ^{-1}(\left\{x\right\})$ donc$\mathbb {P} \left(X\in \partial \psi ^{-1}(\left]x,+\infty \right[)\right)=0$ sauf pour un ensemble au plus dénombrable $D_{0}$ de valeurs de $x$et de même, pour tout $n\geq 1$,$\mathbb {P} \left(X_{n}\in \partial \psi ^{-1}(\left]x,+\infty \right[)\right)=0$ sauf pour un ensemble au plus dénombrable $D_{n}$ de valeurs de $x$.

L'ensemble $\cup _{n\geq 0}D_{n}$ est au plus dénombrable donc Lebesgue-négligeable. Par conséquent, en vertu du point 5 :

pour presque tout $x\in \left[0,1\right]$, $\mathbb {P} \left[\psi (X_{n})>x\right]\to \mathbb {P} \left[\psi (X)>x\right]$.

On conclut par convergence dominée :

$\mathbb {E} \left[\psi (X_{n})\right]=\int _{0}^{1}\mathbb {P} \left[\psi (X_{n})>x\right]\,\mathrm {d} x\to \int _{0}^{1}\mathbb {P} \left[\psi (X)>x\right]\,\mathrm {d} x=\mathbb {E} \left[\psi (X)\right]$.

Enfin, dans le cas général, pour une fonction continue bornée $\varphi$, telle que $a<\varphi <b$, on se ramène au cas précédent en posant

$\psi \ :=\ {\frac {\varphi -a}{b-a}}$

de sorte que $0<\psi <1$.

Historique

D'après Billingsley ou Kallenberg, le théorème porte-manteau est dû à Alexandrov. Dans la deuxième édition de Convergence of Probability Measures, Billingsley attribue le théorème à Jean-Pierre Portmanteau, de l'université de Felletin, dans un article de 4 pages que Jean-Pierre Portmanteau aurait publié en 1915 dans les Annales de l'Université de Felletin, sous le titre farfelu « Espoir pour l'ensemble vide ? ». Il s'agit d'un canular : il n'y a pas de mathématicien portant le nom de Jean-Pierre Portmanteau, et il n'y a jamais eu d'université à Felletin.