Chirurgie (topologie)

En mathématiques, et particulièrement en topologie géométrique, la chirurgie est une technique, introduite en 1961 par John Milnor[1], permettant de construire une variété à partir d'une autre de manière « contrôlée ». On parle de chirurgie parce que cela consiste à « couper » une partie de la première variété et à la remplacer par une partie d'une autre variété, en identifiant les frontières ; ces transformations sont étroitement liées à la notion de décomposition en anses. La chirurgie est un outil essentiel dans l'étude et la classification des variétés de dimension supérieure à 4.
Plus précisément, l'idée est de partir d'une variété qu'on connaît bien, et d'opérer chirurgicalement sur elle pour construire une variété ayant les propriétés que l'on souhaite, de telle sorte que les effets de ces opérations sur les groupes d'homologie, d'homotopie, ou sur d'autres invariants de la variété soient calculables.
La classification des sphères exotiques par Kervaire et Milnor[2] en 1963 amena à l'émergence de la chirurgie comme un outil majeur de la topologie en grande dimension.
Chirurgie sur une variété[modifier | modifier le code]
Dans tout cet article, on note la sphère de dimension p, et la boule (fermée) de dimension p+1 dont est le bord. L'observation fondamentale justifiant la chirurgie est que l'espace peut être vu, soit comme la frontière de , soit comme la frontière de . Par conséquent, étant donné une variété de dimension et un plongement , on peut définir une autre variété de dimension par
On dit que la variété est produite par chirurgie, coupant et collant , ou plus précisément par -chirurgie si l'on veut expliciter . À proprement parler, est une variété à coins, mais il y a une façon canonique de les lisser.
La chirurgie est proche de l'opération d'attachement d'anses (mais ne lui est pas identique). Étant donné une variété à bord de dimension , , et un plongement , on définit une autre variété à bord de dimension , , par
On dit que est obtenue en attachant une -anse, étant obtenue à partir de par la -chirurgie
Une opération de chirurgie sur ne construit pas seulement une nouvelle variété , mais aussi un cobordisme entre et . La cicatrice de l'opération est le cobordisme , où
- ,
la variété de dimension ayant pour bord étant obtenue à partir du produit en attachant une -anse .
La chirurgie est une opération symétrique, en ce que la variété peut être reconstruite à partir de la variété par une -chirurgie, dont la cicatrice coïncide avec celle de la chirurgie initiale (à l'orientation près).
Dans la plupart des applications, la variété possède une structure géométrique supplémentaire, par exemple une application vers un espace de référence, ou la donnée d'une fibration. On veut alors qu'après chirurgie, la variété possède une structure analogue. Par exemple, un outil important de la théorie est la chirurgie sur les applications normales (en) : une telle opération change une application normale en une autre application normale ayant la même classe de bordisme.
Exemples[modifier | modifier le code]
Chirurgie sur le cercle[modifier | modifier le code]
Comme le veut la définition, une chirurgie sur le cercle consiste à couper une copie de et à coller à sa place . La figure 1 montre que le résultat de cette opération est soit à nouveau, soit deux copies de .
-
Figure 1
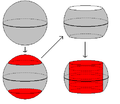
Chirurgie sur la 2-sphère[modifier | modifier le code]
Il y a à présent deux classes de possibilités distinctes, puisqu'on peut couper ou .
- : on retire un cylindre de la 2-sphère, ce qui laisse deux disques. Recollant , c'est-à-dire deux autres disques, il est clair que le résultat est deux sphères disjointes (figure 2a).
- : ayant coupé deux disques , on recolle le cylindre . Cela peut se faire de deux façons différentes, selon l'orientation du recollement sur chacun des disques frontières : si les orientations sont les mêmes (figure 2b), la variété obtenue est le tore ; sinon, on obtient la bouteille de Klein (figure 2c).
-
Figure 2a
-
Figure 2b
-
Figure 2c. Cette variété, isomorphe à une bouteille de Klein, ne peut se plonger dans l'espace usuel.
Fonctions de Morse[modifier | modifier le code]
Soit une fonction de Morse sur une variété de dimension , et une valeur critique dont la pré-image contient un seul point critique. Si l'indice de ce point critique est , alors l'hypersurface de niveau est obtenu à partir de par une -chirurgie, et le bordisme s'identifie à la cicatrice de cette chirurgie.
| Image externe | |
| Figure 3 | |
Plus explicitement, il existe une carte locale autour du point critique dans laquelle la fonction prend la forme , avec , et . La figure 3 montre, dans cette carte locale, la variété en bleu et la variété en rouge. La région colorée entre et correspond au bordisme . On voit sur cette figure que est difféomorphe à l'union (en négligeant le problème du lissage des coins), où est colorée en jaune, et en vert. La variété , étant une composante de la frontière de , s'obtient par conséquent à partir de par une -chirurgie.
Comme chaque bordisme entre variétés fermées correspond à une fonction de Morse dont les différents points critiques ont des valeurs critiques distinctes, il en résulte que tout bordisme peut se décomposer en cicatrices de chirurgies (décomposition en anses). En particulier, toute variété peut être vue comme un bordisme allant de la frontière (qui peut être vide) vers la variété vide, et donc peut être obtenue à partir de en attachant des anses.
Effets sur les groupes d'homotopie, et comparaison avec l'attachement de cellules[modifier | modifier le code]
Intuitivement, la chirurgie est l'analogue, pour les variétés, de l'adjonction d'une cellule à un espace topologique (au sens des complexes simpliciaux, ou des CW-complexes), le plongement remplaçant l'application d'attachement. Coller simplement une -cellule à une -variété détruirait la structure de variété (pour des raisons de dimensions) ; la cellule doit donc être épaissie en en faisant le produit avec une autre cellule.
À homotopie près, la chirurgie sur un plongement peut être décrite comme l'adjonction d'une (p + 1)-cellule, donnant le type d'homotopie de la cicatrice, et l'excision d'une q-cellule pour obtenir . La nécessité de l'excision peut se voir comme un effet de la dualité de Poincaré.
De la même façon qu'on peut attacher une cellule à un espace pour supprimer un élément d'un des groupes d'homotopie de l'espace (intuitivement, cela correspond à « boucher un trou »), une -chirurgie sur une variété peut souvent être utilisée pour supprimer un élément . Il y a cependant deux aspects importants à considérer : d'abord, l'élément doit être représentable par un plongement (la sphère correspondante doit être plongée par l'intermédiaire d'un fibré normal trivial) ; ainsi, il n'est pas possible d'effectuer une opération de chirurgie sur une boucle renversant l'orientation. Ensuite, l'effet de l'opération d’excision doit aussi être pris en compte, puisque cela peut modifier le groupe d'homotopie considéré (ce dernier point n'est important que lorsque est au moins de l'ordre de la moitié de la dimension de ).
Application à la classification des variétés[modifier | modifier le code]
La principale application de la théorie reste la classification des variétés (en) de dimension plus grande que quatre. Les questions centrales auxquelles cherche à répondre la théorie sont :
- Un espace donné X a-t-il le même type d'homotopie qu'une variété différentielle de même dimension ?
- Est-ce qu'une équivalence homotopique donnée entre deux variétés différentielles est homotope à un difféomorphisme ?
La seconde question est d'ailleurs essentiellement une forme plus précise de la première.
La chirurgie ne fournit pas un ensemble complet d'invariants permettant de répondre à ces questions. C'est plutôt une théorie de l'obstruction : on détermine une obstruction primaire, et il apparait une obstruction secondaire appelée l’obstruction chirurgicale (en) qui n'est définie que lorsque l'obstruction primaire est nulle, et qui dépend d'ailleurs des choix faits lors de la vérification de cette nullité.
L'approche chirurgicale[modifier | modifier le code]
Dans l'approche classique, développée par Browder, Novikov, Sullivan et Wall, la chirurgie est faite sur des applications normales (en) de degré 1. Grâce à la chirurgie, la question « L'application normale de degré un est-elle cobordante à une équivalence homotopique ? » peut se traduire (en dimension supérieure à quatre) par une question algébrique concernant un élément d'un L-groupe de l'algèbre du groupe d'homotopie . Plus précisément, la réponse est positive si et seulement si l'obstruction de chirurgie (en) est nulle, n étant la dimension de M.
Par exemple, considérons le cas où la dimension n = 4k est un multiple de 4, et . On sait que est isomorphe à ; par cet isomorphisme, l'obstruction de chirurgie de f est envoyée (à un facteur scalaire près) sur la différence des signatures (en) de X et de M. Par conséquent, une application normale de degré un est cobordante à une équivalence homotopique si et seulement si le domaine et le codomaine ont la même signature.
Revenant à la question d'« existence » posée plus haut, on voit qu'un espace X a le type d'homotopie d'une variété différentielle si et seulement s'il provient d'une application normale de degré 1 dont l'obstruction de chirurgie est nulle. Cela amène à une suite d'obstructions : pour pouvoir parler d'applications normales, il faut que X satisfasse une version appropriée de la dualité de Poincaré, faisant de X un complexe de Poincaré (en). Si X est un complexe de Poincaré, la construction de Pontryagin-Thom (en) montre qu'une application normale de degré un vers X existe si et seulement si la fibration normale de Spivak de X se réduit à un fibré vectoriel stable (en). Si ces applications normales existent, leurs classes de bordisme (appelées invariants normaux) sont classées par les ensembles de classes d'homotopie . Chaque invariant normal a une obstruction de chirurgie ; X est homotope à une variété différentielle si et seulement si l'une de ces obstructions est nulle ; autrement dit, il existe alors un invariant normal dont l'image par l’application d'obstruction de chirurgie est nulle.
Ensembles structuraux et suite exacte de chirurgie[modifier | modifier le code]
La notion d'ensemble structural (en) donne un cadre unifié aux questions d'existence et d'unicité. Schématiquement, l'ensemble structural d'un espace est formé d'équivalences homotopiques d'une variété vers X, deux applications étant identifiées par une relation de bordisme. Une condition nécessaire (mais non suffisante en général) pour que l'ensemble structural de soit non vide est que soit un complexe de Poincaré de dimension , c'est-à-dire que les groupes d'homologie et de cohomologie soient reliés par des isomorphismes d'une variété de dimension . Selon le choix précis de variété (différentielle, linéaire par morceaux ou topologique), il y a plusieurs définitions possibles des ensembles structuraux. Comme, d'après le théorème de s-cobordisme (en), certains bordismes entre variétés sont isomorphes (dans la catégorie correspondante) à des cylindres, les ensembles structuraux permettent une classification même à un difféomorphisme près.
Les ensembles structuraux et les applications d'obstruction de chirurgie sont reliés par la suite exacte de chirurgie (en). Cette suite permet de déterminer l'ensemble structural d'un complexe de Poincaré lorsqu'on connaît l'application d'obstruction de chirurgie. Ce calcul est possible dans de nombreux cas importants, et a permis de classifier les sphères exotiques, ainsi que de démontrer la conjecture de Borel (en) pour les variétés de courbure négative et pour celles de groupe fondamental hyperbolique.
Notes[modifier | modifier le code]
Références[modifier | modifier le code]
- (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Surgery theory » (voir la liste des auteurs).
- (en) William Browder, Surgery on simply-connected manifolds, Berlin, New York, Springer,
- (en) Sylvain Cappell, Andrew Ranicki et Jonathan Rosenberg (eds.), Surveys on surgery theory, vol. 1, PUP, coll. « Annals of Mathematics Studies » (no 145), , 448 p. (ISBN 978-0-691-04938-0, MR 1746325, lire en ligne)
- (en) Sylvain Cappell, Andrew Ranicki et Jonathan Rosenberg (eds.), Surveys on surgery theory, vol. 2, PUP, coll. « Annals of Mathematics Studies » (no 149), , 380 p. (ISBN 978-0-691-08815-0, lire en ligne)
- (en) Michel A. Kervaire et John Willard Milnor, « Groups of homotopy spheres: I », Ann. Math., vol. 77, no 3, , p. 504–537 (DOI 10.2307/1970128, JSTOR 1970128)
- (en) John Willard Milnor, « A procedure for killing homotopy groups of differentiable manifolds », dans Proc. Sympos. Pure Math., Vol. III, Providence, R.I., AMS, , p. 39–55
- (en) John Willard Milnor, Lectures on the h-cobordism theorem : Notes by L. Siebenmann and J. Sondow, PUP,
- (en) M. M. Postnikov et Yu. B. Rudyak, « Morse surgery », dans Michiel Hazewinkel, Encyclopædia of Mathematics, Springer, (ISBN 978-1556080104, lire en ligne)
- (en) Andrew Ranicki, « The algebraic theory of surgery. I. Foundations », Proc. London Math. Soc., vol. 40, no 3, , p. 87–192 (DOI 10.1112/plms/s3-40.1.87, lire en ligne)
- (en) Andrew Ranicki, « The algebraic theory of surgery. II. Applications to topology », Proc. London Math. Soc., vol. 40, , p. 193–283 (DOI 10.1112/plms/s3-40.2.193, lire en ligne)
- (en) Andrew Ranicki, Algebraic and Geometric Surgery, Clarendon Press, coll. « Oxford Mathematical Monographs », , 373 p. (ISBN 978-0-19-850924-0, lire en ligne), MR 2061749
- (en) C. T. C. Wall et Andrew Ranicki (ed.), Surgery on compact manifolds, Providence, R.I., AMS, coll. « Mathematical Surveys and Monographs » (no 69), , 2e éd. (1re éd. 1970), 302 p. (ISBN 978-0-8218-0942-6, lire en ligne)











































![{\displaystyle W:=f^{-1}([c-\epsilon ,c+\epsilon ])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93bf0475121a594432dff533cbe528c78a75af8a)













![{\displaystyle Z[\pi _{1}(X)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67d630a9d81b415e1d875cc350ee9c07b048b806)
![{\displaystyle \sigma (f)\in L_{n}(Z[\pi _{1}X])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9448b7dab70c889064a38885f8adf872930e81a0)




![{\displaystyle [X,G/O]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/569533f20783c1029a1270bae080aaa9325f0586)
![{\displaystyle [X,G/O]\to L_{n}(Z[\pi _{1}(X)])}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4ed6f6a46933b70eb5ac5316a95f4f1f86eb1510)


