Théorème de restriction cristallographique

Le théorème de restriction cristallographique est fondé sur l'observation du fait que les opérations de symétrie rotationnelles d'un cristal sont limitées à des opérations d'ordre 1, 2, 3, 4 et 6. Cependant, les quasi-cristaux, découverts en 1984, peuvent posséder d'autres symétries, comme la rotation d'ordre 5.

Avant la découverte des quasi-cristaux, un cristal était défini comme étant un réseau, généré par une liste de translations finies indépendantes. Parce que la nature discrète du réseau impose une limite inférieure sur la distance entre les nœuds, le groupe des symétries de rotation du réseau en un point quelconque doit être un groupe fini (plus simplement, seul le point possède une infinité de symétries rotationnelles). La conséquence du théorème de restriction cristallographique est que tous les groupes finis ne sont pas forcément compatibles avec un réseau discret : chaque dimension ne possède qu'un nombre fini de groupes compatibles.

Dimensions 2 et 3

Les cas particuliers des dimensions 2 (groupe de papier peint) et 3 (groupes d'espace) sont le plus souvent utilisés et peuvent être traités ensemble.

Preuve dans le réseau

Polygones de restriction cristallographique. Ordres de rotation compatibles : 6 (3), 4 (2) ; incompatibles : 8, 5.

Une symétrie rotationnelle en dimension 2 (2D) ou 3 (3D) doit déplacer un nœud du réseau vers un ensemble d'autres nœuds du réseau dans le même plan, générant un polygone régulier de nœuds coplanaires. Il suffit donc de considérer le plan dans lequel agit l'opération de symétrie.

Considérons maintenant une rotation d'ordre 8 et les vecteurs de translation entre des points adjacents du polygone (en noir sur la figure). Un vecteur de translation doit laisser le réseau invariant lors de l'application de la translation. Si un vecteur de translation existe entre deux nœuds quelconques du réseau, alors ce vecteur doit être présent partout dans le réseau. On peut alors placer l'origine de tous les vecteurs correspondant aux côtés du polygone sur un point du réseau. Ces vecteurs deviennent des vecteurs radials et la symétrie d'ordre 8 impose la présence d'un octogone régulier de points autour du barycentre. Cependant, ceci est impossible, car la taille du nouveau polygone est environ 80 % de celle du polygone de départ. La réduction de la taille du polygone par applications successives de cette procédure est illimitée : la même construction peut être répétée avec le nouvel octogone et ainsi de suite jusqu'à ce que la distance entre deux points devienne infiniment petite. Ainsi, aucun réseau discret ne peut posséder une symétrie rotationnelle d'ordre 8. Le même argument s'applique à toute rotation d'ordre k avec k > 6.

La rotation d'ordre 5 est aussi éliminée par un argument de réduction de taille. Considérons un pentagone régulier de nœuds. Si un tel pentagone existe, alors il est possible de former une étoile à cinq branches avec tous les vecteurs de translation correspondant aux côtés du pentagone. Les sommets de cette étoile forment à nouveau les sommets d'un pentagone régulier, dont la taille est environ 60 % de celle du pentagone de départ.

Ainsi le théorème est prouvé.

L'existence des quasi-cristaux et des pavages de Penrose montre que l'hypothèse d'une translation linéaire est nécessaire. Les pavages de Penrose possèdent une symétrie rotationnelle d'ordre 5 et un ensemble de points discret, les environnements locaux étant répétés à l'infini, mais il n'existe pas de translation linéaire pour l'ensemble du pavage. Sans l'hypothèse d'un réseau discret, la construction ci-dessus ne peut pas conduire à une contradiction et produit même un contre-exemple (non-discret). Ainsi la symétrie rotationnelle d'ordre 5 ne peut pas être éliminée par un argument ne contenant pas l'une de ces hypothèses. Un pavage de Penrose du plan (infini) ne possède qu'un élément de symétrie rotationnelle d'ordre 5 autour d'un seul point, alors que les réseaux plans quadratique (rotation d'ordre 4) et hexagonal (rotation d'ordre 6), par exemple, possèdent une infinité de centres de rotation.

Preuve mathématique simple

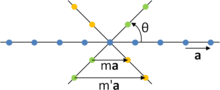
Considérons une ligne du réseau sur laquelle les nœuds sont séparés par le vecteur de translation a. En appliquant une opération de symétrie rotationnelle R d'ordre n (d'angle θ = 360°/n) sur cette ligne, on obtient une ligne de points (en vert sur la figure) séparés par la distance a ; ceci est aussi valable en appliquant l'opération inverse R^–1 d'angle –θ (points orange).

Pour que l'opération R soit une opération de symétrie du réseau, les points obtenus doivent correspondre à des nœuds. En particulier, les vecteurs de translation entre les nœuds des deux nouvelles lignes doivent être des multiples de a : ma, m'a, etc.

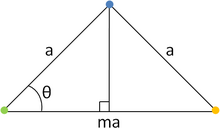
Dans le triangle isocèle de côtés a, a et ma ainsi obtenu, on peut écrire :

$\cos {\theta }={\frac {{\frac {1}{2}}ma}{a}}={\frac {m}{2}}\,,$

m devant être un nombre entier. Comme de plus le cosinus doit être compris entre –1 et +1, il n'y a que cinq possibilités :

m	–2	–1	0	1	2
cos θ	–1	–1/2	0	1/2	1
θ	180°	± 120°	± 90°	± 60°	360°
n	2	3	4	6	1

Preuve matricielle

Pour une preuve alternative, considérons les propriétés des matrices. En dimensions 2 et 3, toutes les rotations agissent dans un plan et la trace de la matrice associée à une rotation ne dépend que de l'angle de rotation θ. La somme des éléments diagonaux d'une matrice est appelée la trace (Tr) de la matrice. Pour une rotation dans l'espace à deux dimensions, la trace de la matrice est $2\cos {\theta }$ ; pour une rotation dans l'espace à trois dimensions, $1+2\cos {\theta }$. Du fait que la rotation doit laisser le réseau invariant, un nœud du réseau doit avoir pour image un autre nœud. La trace de la matrice doit donc être un nombre entier.

Considérons la matrice R associée à une rotation d'angle θ dans une base orthonormale des espaces à deux et trois dimensions :

$R_{2}={\begin{bmatrix}\cos {\theta }&-\sin {\theta }\\\sin {\theta }&\cos {\theta }\end{bmatrix}},\ \ \ R_{3}={\begin{bmatrix}\cos {\theta }&-\sin {\theta }&0\\\sin {\theta }&\cos {\theta }&0\\0&0&1\end{bmatrix}}.$

Par commodité d'écriture, R₃ correspond à une rotation d'angle θ autour de la direction z ; cette convention ne change rien au résultat puisque la trace d'une matrice est invariante par changement de base.

Éléments et trace de la matrice de rotation

n	1	2	3	4	5	6	7	8	9	10
θ	360°	180°	120°	90°	72°	60°	51,4°	45°	40°	36°
cos θ	1	-1	-1/2	0	0,309	1/2	0,623	0,707	0,766	0,809
sin θ	0	0	0,866	1	0,951	0,866	0,782	0,707	0,643	0,588
Tr (R2)	2	-2	-1	0	0,618	1	1,246	1,414	1,532	1,618
Tr (R3)	3	-1	0	1	1,618	2	2,246	2,414	2,532	2,618

Ainsi, par exemple, les cristaux ne peuvent pas présenter une symétrie rotationnelle d'ordre 8. Les seuls angles de rotation possibles sont des multiples de 60° (2π/6), 90° (2π/4), 120° (2π/3), 180° (2π/2) et 360° (2π/1), correspondant à des rotations d'ordre 6, 4, 3, 2 et 1 respectivement.

Le théorème de restriction cristallographique ne garantit cependant pas qu'une rotation soit compatible avec n'importe quel réseau. Par exemple, une rotation d'ordre 6 ne peut pas être présente dans un réseau quadratique, ni une rotation d'ordre 4 dans un réseau orthorhombique.

Dimensions supérieures

Dans un espace de dimension supérieure à 3, les rotations n'agissent plus forcément dans un plan : la preuve du théorème dans l'espace à deux dimensions ne fonctionne plus. Cependant, il y a toujours des restrictions, bien que plus de symétries soient permises. Par exemple, le réseau hypercubique possède une symétrie rotationnelle d'ordre 8 correspondant à celle de l'hypercube. Ceci n'est pas seulement intéressant d'un point de vue mathématique mais aussi pour la physique des quasi-cristaux : un quasi-cristal peut être décrit comme la projection dans l'espace à trois dimensions d'une coupe d'un cristal de dimension 4, possédant par exemple une rotation d'ordre 8. En cristallographie, des groupes d'espace 4D, 5D et même 6D peuvent ainsi être utilisés pour décrire les structures modulées.

La matrice de rotation 4D suivante correspond à la rotation d'ordre 8 de l'hypercube (et du polytope croisé) dans le système de coordonnées cristallographique :

$A={\begin{bmatrix}0&0&0&-1\\1&0&0&0\\0&-1&0&0\\0&0&-1&0\end{bmatrix}}.$

Le changement de base vers une autre base orthonormée par la matrice de passage (orthogonale)

$B={\begin{bmatrix}-1/2&0&-1/2&{\sqrt {2}}/2\\1/2&{\sqrt {2}}/2&-1/2&0\\-1/2&0&-1/2&-{\sqrt {2}}/2\\-1/2&{\sqrt {2}}/2&1/2&0\end{bmatrix}}$

donne :

$BAB^{-1}={\begin{bmatrix}{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\-{\sqrt {2}}/2&{\sqrt {2}}/2&0&0\\0&0&-{\sqrt {2}}/2&{\sqrt {2}}/2\\0&0&-{\sqrt {2}}/2&-{\sqrt {2}}/2\end{bmatrix}}.$

Cette troisième matrice correspond à une rotation de 45° dans les deux premières dimensions et de 135° dans les deux autres. La projection d'une coupe d'hypercube le long des deux premières dimensions du nouveau système de coordonnées produit un pavage d'Ammann–Beenker (en) (ainsi que la projection le long des deux autres dimensions), qui possède donc en moyenne une symétrie rotationnelle d'ordre 8.

Les réseaux A4 et F4 possèdent des symétries rotationnelles d'ordre 10 et 12 respectivement.

Afin de trouver les restrictions pour toutes les dimensions, il est préférable, au lieu de considérer les rotations, de se concentrer sur les matrices entières (c'est-à-dire : à coefficients entiers). En effet, pour tout réseau, il existe une base (non orthonormée en général) dans laquelle toutes les symétries du réseau sont représentées par des matrices entières. On dit qu'une matrice A est d'ordre k quand sa puissance k^e, A^k, est égale à l'identité (k étant le plus petit entier satisfaisant cette relation). Ainsi la matrice correspondant à une rotation d'ordre 6 est une matrice d'ordre 6 (dans n'importe quelle base) et entière (dans une base bien choisie). Soit Ord_N l'ensemble des entiers qui peuvent être l'ordre d'une matrice entière N×N. Par exemple, Ord₂ = {1, 2, 3, 4, 6}. Le but est trouver une formule explicite pour Ord_N.

Définissons une fonction ψ basée sur l'indicatrice d'Euler φ ; à tout entier naturel non nul elle associe un entier naturel. Pour un nombre premier impair p et un entier k strictement positif, posons ψ(p^k) égal à l'indicatrice d'Euler, φ(p^k), qui est dans ce cas p^k−p^k-1. Faisons de même pour ψ(2^k) quand k > 1. Posons ψ(2)=0 et ψ(1)=0. En utilisant le théorème fondamental de l'arithmétique, on peut écrire de façon unique tout entier naturel m non nul comme un produit fini de puissances de nombres premiers,

$m=\prod _{\alpha }p_{\alpha }^{k_{\alpha }}.$

On pose alors

$\psi (m)=\sum _{\alpha }\psi (p_{\alpha }^{k_{\alpha }})~.$

Ceci est différent de l'indicatrice elle-même, puisqu'il s'agit d'une somme et non d'un produit.

La restriction cristallographique dans sa forme générale affirme que Ord_N est constitué des entiers positifs m tels que ψ(m) ≤ N.

Plus petite dimension pour un ordre donné

m	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21	22	23	24	25	26	27	28	29	30	31
ψ(m)	0	0	2	2	4	2	6	4	6	4	10	4	12	6	6	8	16	6	18	6	8	10	22	6	20	12	18	8	28	6	30

Notons que ces symétries supplémentaires ne permettent pas à une coupe plane de posséder, par exemple, une symétrie rotationnelle d'ordre 8. Dans le plan, les restrictions 2D sont toujours en vigueur. Ainsi, les coupes utilisées pour modéliser les quasi-cristaux doivent avoir une épaisseur.

Les matrices entières ne sont pas limitées aux rotations ; par exemple, une réflexion est aussi une opération de symétrie d'ordre 2. En imposant à la matrice d'être de déterminant égal à +1, il est possible de ne retenir que les rotations pures.

Formulation en termes d'isométries

Le théorème de restriction cristallographique peut être formulé en termes d'isométries de l'espace euclidien. Un ensemble d'isométries peut former un groupe. Un groupe discret d'isométries signifie ici un groupe d'isométries qui fait correspondre chaque point vers un sous-ensemble discret de R_N, c'est-à-dire un ensemble de points isolés. Avec cette terminologie, le théorème de restriction cristallographique pour les dimensions 2 et 3 peut être formulé comme suit :

Pour chaque groupe discret d'isométries dans l'espace à deux et trois dimensions qui inclut les translations sur tout l'espace, toutes les isométries d'ordre fini sont d'ordre 1, 2, 3, 4 ou 6.

Notons que les isométries d'ordre n incluent, mais pas uniquement, les rotations d'ordre n. Le théorème exclut aussi S₈, S₁₂, D_4d et D_6d (voir la notation de Schoenflies).

Notons aussi qu'une opération de symétrie rotationnelle d'ordre quelconque autour d'un axe est compatible avec une symétrie translationnelle le long de cet axe.

D'après le tableau ci-dessus, pour chaque groupe discret d'isométries dans l'espace à 4 et 5 dimensions qui inclut les translations sur tout l'espace, toutes les isométries d'ordre fini sont d'ordre 1, 2, 3, 4, 5, 6, 8, 10, or 12.

Toutes les isométries d'ordre fini dans l'espace à 6 et 7 dimensions sont d'ordre 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 18, 20, 24 or 30.

Notes et références

• (en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Crystallographic restriction theorem » (voir la liste des auteurs).

Bibliographie

• (en) Stephen Elliott, The Physics and Chemistry of Solids, Wiley, 1998, 794 p. (ISBN 0-471-98194-X)

Voir aussi

Articles connexes

• Groupe de symétrie
• Groupe ponctuel de symétrie
• Cristallographie

Lien externe

(en) John J. O'Connor et Edmund F. Robertson, « The crystallographic restriction », sur MacTutor, université de St Andrews.