Théorème de Brooks

Un article de Wikipédia, l'encyclopédie libre.
Le graphe de Petersen a pour degré maximal (et minimal) 3. On peut effectivement le colorer avec 3 couleurs.

En mathématiques, et plus particulièrement dans la théorie des graphes, le théorème de Brooks donne une relation entre le degré maximal d'un graphe connexe non orienté et son nombre chromatique.

Selon ce théorème, dans un graphe où chaque sommet a au plus Δ voisins, les sommets peuvent être colorés avec au plus Δ couleurs, sans que deux sommets adjacents n'aient la même couleur, sauf dans deux cas, les graphes complets et les graphes cycles de longueur impaire, qui ont besoin de Δ + 1 couleurs.

Énoncé[modifier | modifier le code]

Théorème — Dans tout graphe connexe non orienté G de degré maximal Δ, le nombre chromatique χ(G) vérifie χ(G) ≤ Δ, sauf si G est un graphe complet ou un cycle de longueur impaire, auquel cas χ(G) = Δ + 1.

Histoire et contexte[modifier | modifier le code]

Le théorème porte le nom de R. Leonard Brooks, qui en a publié une démonstration en 1941[1]. Une coloration avec le nombre de couleurs décrit par le théorème de Brooks est parfois appelée coloration de Brooks ou Δ-coloration. László Lovász a donné une démonstration plus simple du théorème en 1975[2].

Il n'est pas très dur de démontrer que, pour tout graphe, χ(G) ≤ Δ + 1. En effet, n'importe quel sommet v possède au maximum Δ sommets voisins, qui dans le pire des cas sont tous de couleur différente. Même dans ce cas, on peut toujours prendre la (Δ + 1)ème couleur pour colorer v. Le mérite de Brooks a été de diminuer cette majoration de 1 unité dans la plupart des cas.

Démonstration[modifier | modifier le code]

Il existe plusieurs démonstrations du théorème de Brooks. On peut par exemple raisonner par récurrence sur le nombre de sommets du graphe. La démonstration qui suit procède autrement, elle s'appuie sur l'algorithme glouton de coloration des graphes et a donc le mérite de donner des algorithmes pour colorer le graphe (c'est une démonstration constructive).

Cette démonstration a été présentée par Ross Churchley en 2010[3] d'après les travaux de John Adrian Bondy en 2003[4]. La fin remplace le raisonnement de Bondy par d'autres travaux pour ne pas avoir à faire appel aux résultats concernant les arbres de parcours en profondeur d'abord.

Dans ce qui suit, nous examinons successivement quatre cas :

  • les graphes non réguliers ;
  • les graphes réguliers non biconnexes ;
  • les graphes réguliers biconnexes de degré inférieur à 3 ;
  • les graphes réguliers biconnexes de degré supérieur ou égal à 3.

Cas des graphes non réguliers[modifier | modifier le code]

Le principe, dans le cas des graphes non réguliers, est d'ordonner les sommets d'une certaine façon, et ensuite de les colorer l'un après l'autre à l'aide de l'algorithme glouton.

Numérotation, puis coloration d'un graphe non régulier de degré maximal 4.

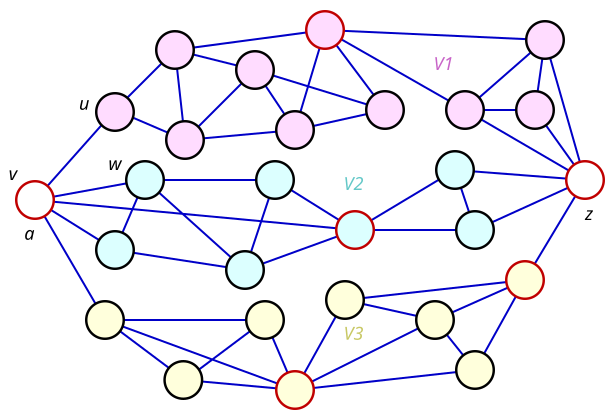
Soit G un graphe non régulier à n sommets et de degré maximal Δ. Comme G n'est pas régulier, il existe au moins un sommet x de degré s strictement inférieur à Δ. On place ce sommet à la fin de l'ordonnancement, c'est-à-dire vn = x (figure 1). Les sommets adjacents à x sont placés juste avant dans cet ordonnancement, c'est-à-dire en vn-s, vn-s-1, …, vn-1 (figure 2).

On considère ensuite les sommets adjacents à vn-1 qui n'ont pas déjà été ordonnés (figure 3), puis ceux qui sont adjacents à vn-2 et qui n'ont pas encore été ordonnés, et ainsi de suite jusqu'à les ordonner tous, ce qui est possible puisque G est connexe (figure 4).

Dans cet ordonnancement (v1, v2, …, vn), tous les sommets ont au moins un sommet adjacent postérieur (d'indice supérieur), sauf le sommet x. Par conséquent, ils ont tous, sauf le sommet x, un nombre de sommets adjacents antérieurs (d'indice inférieur) strictement inférieur à Δ. Le dernier sommet x a aussi, de par son choix initial, un nombre de sommets adjacents antérieurs strictement inférieur à Δ.

On colore ensuite les sommets vi les uns après les autres, pour i variant de 1 à n. À chaque étape, le sommet vi n'a pas encore été coloré. Ses sommets adjacents antérieurs, qui ont déjà été colorés, sont au maximum au nombre de Δ − 1, et utilisent donc a fortiori au maximum Δ − 1 couleurs. On peut donc prendre pour le nouveau sommet, dans le pire des cas, la couleur restante parmi Δ (figures 5 à 8).

Cas des graphes réguliers non biconnexes[modifier | modifier le code]

Dans un graphe non biconnexe, il existe au moins un point d'articulation, c'est-à-dire un sommet qui, s'il est retiré, rend le graphe non connexe.

Coloration d'un graphe 3-régulier non biconnexe.

Considérons un tel graphe G régulier de degré Δ non biconnexe et soit x un point d'articulation de G (en rouge sur la figure 1).

On décompose G en démultipliant le point d'articulation comme sur la figure 2. On obtient au moins deux graphes non réguliers connexes de degré maximal Δ : en effet, les sommets obtenus en démultipliant x sont chacun de degré strictement inférieur à Δ.

On est donc ramené au cas précédent et on peut colorer chaque composante connexe non régulière en utilisant la méthode exposée auparavant. On peut s'arranger pour que les sommets obtenus en démultipliant x aient la même couleur : pour cela, on permute les couleurs au sein des composantes connexes si c'est nécessaire.

Il ne reste plus qu'à réassembler les parties de graphe pour obtenir un graphe coloré avec Δ couleurs.

Cas des graphes réguliers biconnexes de degré inférieur à 3[modifier | modifier le code]

Le seul graphe régulier de degré 0 qui soit connexe est le graphe 0-régulier composé d'un seul sommet. Il peut être coloré avec 1 couleur (figure 1). Comme il entre dans la catégorie des graphes complets, il vérifie l'énoncé du théorème de Brooks.

Le seul graphe régulier de degré 1 qui soit connexe est le graphe 1-régulier constitué de deux sommets seulement, avec une arête entre ces deux sommets (figure 2). Il peut être coloré avec 2 couleurs et là aussi on est dans le cas d'un graphe complet : il vérifie l'énoncé du théorème de Brooks.

Les seuls graphes réguliers connexes de degré 2 sont les cycles. Les cycles comportant un nombre de sommets pair peuvent être colorés avec 2 couleurs (figure 4), et il faut 3 couleurs pour les cycles comportant un nombre de sommets impair (figures 3 et 5). Dans les deux cas, l'énoncé du théorème de Brooks est vérifié.

Coloration des graphes réguliers connexes de degré 0, 1 ou 2.

Cas des graphes réguliers biconnexes de degré supérieur ou égal à 3[modifier | modifier le code]

Si le graphe G est complet et de degré Δ, il comporte Δ + 1 sommets que l'on peut chacun colorer avec une couleur différente. Dans ce cas aussi, l'énoncé du théorème de Brooks est vérifié.

Si le graphe n'est pas complet, on va de nouveau ordonner un certain nombre de sommets, puis les colorer à l'aide de l'algorithme glouton. Ce n'est toutefois pas aussi simple que dans le cas du graphe non régulier, car rien ne nous garantit a priori de disposer d'une couleur de libre quand on arrive au dernier sommet. On va donc s'arranger pour que le dernier sommet v coloré ait deux voisins u et w déjà colorés dans la même couleur, ce qui assure qu'on aura au moins encore une couleur de libre lorsqu'il s'agira de colorer v.

Soit G un graphe non complet, biconnexe, et de degré Δ ≥ 3. Il existe trois sommets u, v et w tels que

  • u est relié à v ;
  • v est relié à w ;
  • mais u n'est pas relié à w.
Démonstration
Lemme 1
Dans un graphe G connexe et non complet, on peut trouver des sommets u et w voisins d'un même sommet v, mais non voisins entre eux.

Comme G n'est pas complet, il existe deux sommets a et b qui ne sont pas directement reliés par une arête. Comme le graphe est connexe, il existe un chemin (a, v1, v2, …, vp, b) reliant a à b. Soit i la plus grande valeur telle que vi soit relié à a. Prenons u = a, v = vi et w = vi+1. Ces trois sommets vérifient bien que u et w sont liés à v sans être liés entre eux.

Dans un graphe connexe et non complet, on peut trouver u, v et w tels que u et w soient des voisins de v, mais ne soient pas voisins entre eux.

Comme le graphe est biconnexe, on peut en retirer u ou w sans qu'il cesse d'être connexe : G - { u } et G - { w } sont connexes. On peut même s'arranger pour prendre u, v et w tels que G - { u, w } soit encore connexe.

Démonstration
Lemme 2
Dans un graphe G biconnexe, de degré minimal 3 ou plus et non complet, on peut trouver des sommets u et w voisins d'un même sommet v, mais non voisins entre eux, tels que G - { u, w } est encore connexe[5],[6].

Comme le graphe n'est pas complet, il existe au moins un sommet a qui n'est pas adjacent à tous les autres.

Si G - { a } est biconnexe, on prend, comme dans la démonstration du Lemme 1, u = a et w égal à n'importe quel sommet à une distance 2 de a. Comme G - { a } est biconnexe, on peut en retirer w sans perdre la connexité, et G - { u, w } est connexe.

Considérons à présent le cas où G - { a } est connexe, mais non biconnexe. Il comporte donc des points d'articulation (en rouge sur la figure). Soit z un de ces points d'articulation. G - { a, z } est non connexe, il est même découpé en au moins deux composantes connexes disjointes. Chacune de ces composantes connexes V1, V2, … Vn peut à son tour être découpée en composantes biconnexes reliées par les points d'articulation. Ces composantes biconnexes forment un arbre de racine z.

Un graphe biconnexe qui devient non connexe quand on supprime deux de ses sommets a et z.

Dans G, a possède un voisin dans chacune des feuilles à l'extrémité de cet arbre. En effet, si l'on enlève le point d'articulation zi à laquelle est accrochée la feuille, si elle n'était pas reliée à a à l'autre bout, G - { zi } serait non connexe, ce qui est impossible, puisque G est biconnexe.

Prenons u dans une des feuilles au bout de V1 et w dans une des feuilles au bout de V2 et posons v = a. Les sommets u et w sont bien voisins de v. Ils ne sont pas adjacents, puisqu'ils sont pris dans des composantes connexes différentes.

Les sommets u et w étant pris dans des composantes biconnexes de G - { a } tout en étant différents des points d'articulation de G - { a }, G - { a, u, w } reste connexe. Comme, de plus, le degré de a est supérieur ou égal à 3, il existe un troisième sommet permettant de relier a à G - { a, u, w }. Le graphe G - { u, w } est donc connexe.

Comme G - { u, w } est connexe, on peut l'ordonner comme dans les cas précédents en donnant à v le numéro le plus fort. On colore ensuite G de la manière suivante :

  • on colore u et w avec la même couleur, ce qui est possible puisqu'ils ne sont pas reliés (figure 1) ;
  • on colore ensuite le reste du graphe en respectant l'ordre que l'on vient d'établir. Comme chacun des sommets sauf le dernier possède au moins un voisin non coloré, il possède au plus Δ − 1 voisins colorés et peut être coloré en restant dans les Δ couleurs imposées.

Coloration d'un graphe régulier biconnexe de degré au moins 3 et non complet.

Lorsqu'on en arrive à colorer le dernier sommet v, on a la garantie qu'il reste une couleur de libre, puisque ses deux voisins u et w ont la même couleur (figure 2).

Résultats voisins[modifier | modifier le code]

Une généralisation du théorème de Brooks s'applique à la coloration par liste : étant donné un graphe non orienté et connexe de degré maximal Δ qui n'est ni un graphe complet ni un cycle de longueur impaire, et une liste de Δ couleurs pour chaque sommet, il est possible de choisir une couleur pour chaque sommet prise dans sa liste de manière que deux sommets adjacents n'aient jamais la même couleur. En d'autres termes, le nombre chromatique de liste d'un graphe connexe non orienté n'est jamais plus grand que Δ, sauf dans le cas d'un graphe complet ou d'un cycle de longueur impaire. Cela a été démontré par Vadim Vizing en 1976[7].

Avec certains graphes, on a même besoin de moins de Δ couleurs. Bruce Reed montre que Δ − 1 couleurs suffisent si et seulement si le graphe n'a pas de Δ-clique lorsque Δ est suffisamment grand[8]. Pour les graphes sans triangle (sans ensemble de trois sommets adjacents deux à deux), ou plus généralement les graphes où le voisinage de chaque sommet est suffisamment creux, O(Δ / log Δ) couleurs suffisent[9].

Le degré d'un graphe apparaît aussi dans les bornes supérieures du nombre de couleurs nécessaires à d'autres types de colorations :

  • dans la coloration des arêtes d'un graphe, le résultat selon lequel l'indice chromatique est inférieur ou égal à Δ + 1 est le théorème de Vizing;
  • une extension du théorème de Brooks à la coloration totale (en) d'un graphe qui affirme que le nombre chromatique total est au maximum Δ + 2, a été conjecturée par Behzad et Vizing ;
  • le théorème de Hajnal-Szemerédi sur la coloration équitable d'un graphe affirme que tout graphe peut être coloré avec au plus Δ + 1 couleurs de manière que le nombre de sommets de chaque couleur ne diffère au maximum que de 1.

Algorithmes[modifier | modifier le code]

Une coloration avec Δ couleurs, ou même une coloration par liste avec Δ couleurs, d'un graphe de degré maximal Δ peut être obtenue dans un temps linéaire (proportionnel au nombre de sommets et d'arêtes)[10]. Des algorithmes efficaces qui permettent de trouver des colorations de Brooks en utilisant des traitements parallèles ou distribués sont également connus[11],[12],[13],[14].

Notes et références[modifier | modifier le code]

  1. ↑ (en) R. L. Brooks, « On colouring the nodes of a network », Proc. Cambridge Philosophical Society, Math. Phys. Sci., vol. 37,‎ , p. 194-197 (lire en ligne).
  2. ↑ (en) L. Lovász, « Three short proofs in graph theory », J. Combin. Th., Series B, vol. 19,‎ , p. 269–271 (DOI 10.1016/0095-8956(75)90089-1)
  3. ↑ (en) Ross Churchley, « Graph theory haiku - Three short and beautiful proofs », novembre 2010.
  4. ↑ (en) J. A. Bondy, « Short proofs of classical theorems », Journal of Graph Theory, vol. 44, no 3,‎ , p. 159 à 165
  5. ↑ (en) Bradley Baetz et David R. Wood, « Brooks' Vertex-Colouring Theorem in Linear Time, Technical Report CS-AAG-2001-05, The University of Sidney, octobre 2001.
  6. ↑ (en) Dieter Jungnickel, « Graphs, Networks and Algorithms », Volume 5, Second Edition, Springer Verlag, mai 2003, (ISBN 3-540-63760-5).
  7. ↑ (ru) V. G. Vizing, « Vertex colorings with given colors », Diskret. Analiz., vol. 29,‎ , p. 3–10
  8. ↑ (en) Bruce Reed, « A strengthening of Brooks' theorem », J. Combin. Th., Series B, vol. 76, no 2,‎ , p. 136–149 (DOI 10.1006/jctb.1998.1891)
  9. ↑ (en) Noga Alon, Michael Krivelevich et Benny Sudakov, « Coloring graphs with sparse neighborhoods », J. Combin. Th., Series B, vol. 77, no 1,‎ , p. 73–82 (DOI 10.1006/jctb.1999.1910)
  10. ↑ (en) San Skulrattanakulchai, « Δ-List vertex coloring in linear time », Inf. Process. Lett., vol. 98, no 3,‎ , p. 101–106 (DOI 10.1016/j.ipl.2005.12.007)
  11. ↑ (en) H. J. Karloff, « An NC algorithm for Brooks' theorem », TCS, vol. 68, no 1,‎ , p. 89–103 (DOI 10.1016/0304-3975(89)90121-7)
  12. ↑ (en) Péter Hajnal et Endre Szemerédi, « Brooks coloring in parallel », SIAM J. Discrete Math., vol. 3, no 1,‎ , p. 74–80 (DOI 10.1137/0403008)
  13. ↑ (en) Alessandro Panconesi et Aravind Srinivasan, « The local nature of Δ-coloring and its algorithmic applications », Combinatorica, vol. 15, no 2,‎ , p. 255–280 (DOI 10.1007/BF01200759)
  14. ↑ (en) David A. Grable et Alessandro Panconesi, « Fast distributed algorithms for Brooks-Vizing colourings », dans SODA '98: Proceedings of the 9th Annual ACM-SIAM Symposium on Discrete Algorithms, Philadelphia, PA, USA, SIAM, coll. « Journal of Algorithms » (no 37), (DOI 10.1006/jagm.2000.1097, lire en ligne), p. 473–480

Lien externe[modifier | modifier le code]

(en) Eric W. Weisstein, « Brooks' Theorem », sur MathWorld

Ce document provient de « https://fr.wikipedia.org/w/index.php?title=Théorème_de_Brooks&oldid=187876408 ».