Symédiane

Définition

En géométrie, les symédianes d'un triangle sont les droites symétriques des médianes par rapport aux bissectrices.

La symédiane en un sommet A d'un triangle est l'isogonale de la médiane par rapport aux côtés de l'angle Â.

Les symédianes (en jaune) sont les symétriques des médianes (en vert) par rapport aux bissectrices (en pointillés). Les symédianes se coupent au point de Lemoine du triangle.

Point de Lemoine

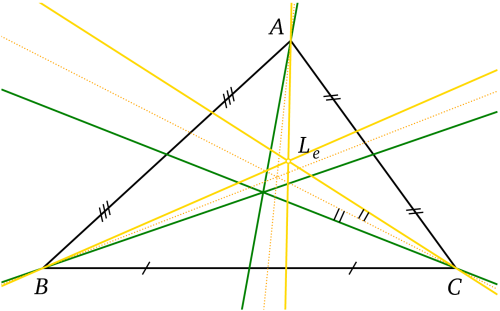
Émile Lemoine a démontré que les trois symédianes d'un triangle sont concourantes. Leur point d'intersection s'appelle le point de Lemoine du triangle $ABC$. De ce fait, c'est le conjugué isogonal du centre de gravité $G$ du triangle.

Il s'ensuit que le point de Lemoine est le barycentre des points pondérés : $(A,a^{2})$, $(B,b^{2})$ et $(C,c^{2})$.

Les distances de ce point aux trois côtés du triangle sont proportionnelles à ces côtés.

C'est le point dont la somme des carrés des distances aux côtés du triangle est minimale.

Ce point est aussi appelé point de Grèbe par les auteurs allemands.

Droite de Lemoine

La droite de Lemoine du triangle est la polaire du point de Lemoine par rapport au cercle circonscrit du triangle. C'est sur cette droite que repose aussi les trois centres des cercles d'Apollonius, cercles correspondants aux triplets (A, B, CA/CB), (B, C, AB/AC) et (C, A, BC/BA).

Milieu d'une antiparallèle

La symédiane coupe une antiparallèle au côté opposé en son milieu.

Milieu d'une symédiane

Milieu d'une symédiane

En effet, dans le triangle ABC, soit (DE) une antiparallèle à (BC) qui coupe la symédiane de issue du sommet A en M. L'antiparallèle (DE) est parallèle à la tangente en A au cercle circonscrit de ABC.

Par la symétrie d'axe la bissectrice (AI) de BÂC, les points D, M, E ont pour images D’, M’, E’. (D’E’) est parallèle à (BC). M’, situé sur la médiane [AA’], est le milieu de [D’E’]. Par symétrie réciproque, M est le milieu de [DE].

Autre démonstration

Dans le triangle ABC, soit M le milieu de (DE) une antiparallèle à (BC). Montrons que (AM) est la symédiane passant par A :

En effet, la droite (AM) est conjuguée harmonique de la tangente en A à (Γ) par rapport à (AB, AC). La droite (AM) est donc la polaire, par rapport à (Γ) du point T, intersection de (BC) avec la tangente en A à (Γ). Par réciprocité polaire, la droite (AM) contient le pôle T1 de (BC). (AM) est la symédiane issue de A.

Application : cercles de Tücker

Références

• Jean-Denis Eiden, Géométrie analytique classique, Calvage & Mounet, 2009, ISBN 978-2-916352-08-4