Sustentation électromagnétique

La sustentation électromagnétique est une méthode permettant de faire léviter un objet en le faisant reposer sur un champ magnétique. Les forces magnétiques appliquées à cet objet s'opposent ainsi à l'action de son propre poids, empêchant sa chute.
Il existe deux concepts fondamentaux concernant la physique et les propriétés de lévitation de la matière :
- le concept électromagnétique (EML) : la lévitation est générée par des électroaimants régulés. Le Transrapid (allemand) et le Swissmetro sont des trains basés sur le concept EML ;
- le concept électrodynamique (EDL) : la lévitation est basée sur les forces de répulsion générées par les courants induits (dits courants de Foucault) qui n'apparaissent que lors d'un déplacement relatif des corps en présence. Il est donc nécessaire de propulser initialement le train avant qu'il puisse léviter magnétiquement. Le seul projet actuellement très avancé utilisant ce concept de sustentation est le Maglev japonais.
Aujourd'hui, la plus grande utilisation de dispositifs à sustentation magnétique pilotée est la pompe à vide secondaire. La production annuelle de ces machines devrait représenter plus de 10 000 unités.
Introduction[modifier | modifier le code]

Le procédé de mise en lévitation magnétique proposé[1] présente une technique très simple en principe, mais qui peut s’avérer délicate en pratique lorsque l'on prend en considération des perturbations externes agissant sur le système.
L’objectif principal de ce projet est de maintenir une charge pour que celle-ci reste en lévitation en se basant sur un modèle complet du système de lévitation ; en déterminant les paramètres qui caractérisent chaque élément qui constitue la plateforme de lévitation magnétique. Le but alors de ce travail est de concevoir un compensateur à avance de phase (lead compensator) afin de rendre le système plus performant au niveau de sa stabilité.

Modélisation du système par la loi de physique[modifier | modifier le code]
Kap, Kea, xap et xea sont les paramètres de l'aimant et de l'électroaimant. M est la masse de la charge et g, la constante de gravité.
L'équation dynamique du système doit être linéarisée afin d'étudier la stabilité du système à un point d'équilibre bien déterminé.
Pour cela on doit linéariser le modèle au complet du système, concernant le capteur de position, le modèle dynamique, et la partie du contrôleur (hacheur et PWM).
Modélisation du système linéaire par résolution numérique informatique[modifier | modifier le code]
La simulation du système montre que ce dernier est à la limite de stabilité, c'est-à-dire le système diverge si on applique une petite perturbation externe, ce que montre la figure de simulation.
Alors pour ramener le système à la stabilité globale, on doit concevoir un compensateur à avance de phase.
Conception du contrôleur à avance de phase[modifier | modifier le code]
La conception du compensateur vient d’améliorer la stabilité de système de telle sorte à déplacer tous les pôles dans le demi-plan à gauche.
Il existe plusieurs méthodes pour déterminer les paramètres du compensateur. Premièrement, on cherche un pôle désiré pour que le lieu géométrique passe par ce pôle, pour cela on impose certains critères de performance comme le temps de stabilisation, le dépassement et l’erreur stationnaire. Lorsque l'on fixe le pôle désiré, on cherche la contribution de l’angle du compensateur qui représente l’angle manquant pour que le lieu géométrique passe par le pôle désiré, pour cela on applique le critère de phase. La méthode la plus simple consiste à imposer le pôle et le zéro du compensateur de telle façon que l'on place le zéro du compensateur en dessous du pôle désiré sur l’axe réel et on cherche ensuite la position du pôle. Finalement, on détermine le gain du compensateur en appliquant le critère du module.
-
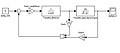
Diagrame de la modélisation
-
Le système n'est pas métastable
-
Position du pôle.
-
Paramètres (pôle et zéro) du compensateur.
-
Simulation du système avec compensateur à avance de phase.
Notes et références[modifier | modifier le code]
- K. H. Lundberg, K. A. Lilienkamp and G. Marsden, “Low-Cost Magnetic Levitation Project Kits”, IEEE Control Systems Magazine, Octobre 2004, pp. 65 - 69.
Voir aussi[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- K. Ogata, Modern Control Engineering, 4e édition.
Liens externes[modifier | modifier le code]
- Train à lévitation magnétique, Département de physique de l'université de Sherbrooke
- (en) Transrapid allemand
- (en) Maglev
- (en) Sur les problèmes de stabilité des objets en lévitation
- (en) magnetbahnforum