Radiosité (infographie)

La radiosité, ou plus exactement la radiance, est une technique de calcul d'éclairage (ou illumination) d'une scène 3D. Elle utilise les formules physiques de transfert radiatif de la lumière entre les différentes surfaces élémentaires composant la scène.

L'illumination est dite globale car l'illumination de chaque surface élémentaire ne peut être calculée séparément des autres et le système modélisant l'ensemble des transferts ne peut être rendu que globalement.

La radiance ne permet pas de calculer directement une image, il s'agit d'une technique d'illumination au même titre que l'algorithme de Phong ou que l'algorithme de Gouraud qui sont eux des techniques d'illumination locales. Pour cela la radiance est souvent associée au lancer de rayon (raytracing) ou encore au Z-buffer qui permettent de créer des images visibles à partir de ses calculs.

La radiance permet de produire des éclairages d'un grand réalisme mais au prix d'une grande complexité de calcul.

La radiance n'est pas encore accélérée matériellement (2011).

Néologie et terminologie[modifier | modifier le code]

Le terme radiosité n'est pas accepté officiellement en français, car étymologiquement incorrect : radiosité, accepté comme néologisme, ne pourrait signifier que le caractère de ce qui est radieux, pas radial ni rayonnant^{[réf. souhaitée]}.

Techniques de radiance[modifier | modifier le code]

Il existe principalement deux techniques pour résoudre une illumination globale. Une résolution type Monte Carlo ou une résolution par le calcul des « coefficients angulaires » (base de la technique des hémicubes). Ces deux techniques présentent chacune avantages et inconvénients. Il est également possible de tirer profit des deux techniques à la fois pour obtenir une méthode précise et efficace.

Light Tracing[modifier | modifier le code]

L'idée est très simple, on lance des rayons aléatoirement depuis une source de lumière (qui peut être décrite par une surface par exemple) selon une certaine distribution angulaire (on utilise classiquement une distribution proportionnelle à une puissance du cosinus de l'angle par rapport à la normale de la surface au point d'émission). On calcule ensuite l'intersection de ces rayons avec les objets de la scène et on les fait rebondir aléatoirement en respectant la distribution angulaire de la diffusion (proportionnelle au cosinus de l'angle avec la normale) et les spectres d'émission/absorption. Chaque fois qu'un rayon est absorbé, on recommence de la source. Il suffit ensuite d'incrémenter chaque élément de surface (texel) lorsque celui-ci est touché, on normalise chaque texel par rapport à sa surface visible et au bout d'un très grand nombre de rayons on obtient le résultat. L'image ci-contre montre une scène de ~170 000 texels obtenue après 37 millions de rayons dont 9 millions au départ de la source. Cette image a demandé environ trois minutes de calcul sur un Quad Core 2,4 GHz. On voit encore nettement le bruit dû au procédé de calcul. La méthode converge naturellement et ce bruit s'atténue lentement avec le nombre de rayons, l'erreur commise est proportionnelle à 1/ ${\sqrt {n}}$ où n représente le nombre de rayons au départ de la source. L'image finale a demandé ~7 heures de calcul (5,1 milliards de rayons). On peut également appliquer des filtres de lissage sur les textures afin d'obtenir un résultat « lissé » plus rapidement. Il existe de nombreux articles sur internet qui traitent des différentes techniques nécessaires. Cependant, la génération aléatoire d'une distribution angulaire proportionnelle à une puissance de cosinus n'est pas souvent évoquée.

Distribution angulaire[modifier | modifier le code]

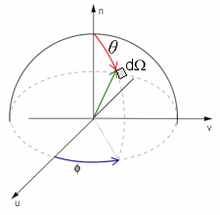
Le plan (u,v) est tangent à la surface, le vecteur n est normal. On utilise le système de coordonnées sphériques. Le but est de générer aléatoirement une direction respectant la distribution angulaire souhaitée (les positions de départ, quand la surface est une source, sont généralement réparties uniformément) :

Angle solide :

$\displaystyle d\Omega =\sin \theta d\phi d\theta$

Proportionnel à $\cos ^{n}\theta$

$\displaystyle d\Omega _{n}=\alpha \cos ^{n}\theta \sin \theta d\phi d\theta$

Normalisation sur la surface visible :

$\displaystyle \int _{\Omega }d\Omega _{n}=2\pi$

$\displaystyle \int _{0}^{2\pi }\int _{0}^{\frac {\pi }{2}}\alpha \cos ^{n}\theta \sin \theta d\theta d\phi =2\pi$

$\displaystyle \int _{0}^{\frac {\pi }{2}}\alpha \cos ^{n}\theta \sin \theta d\theta =1$

$\displaystyle \alpha \left[{\frac {-1}{n+1}}cos^{n+1}\theta \right]_{0}^{\frac {\pi }{2}}=1$

$\displaystyle \alpha =n+1$

Ce qui donne la densité de probabilité de $\theta$ :

$\displaystyle p(\theta )=(n+1)\sin \theta \cos ^{n}\theta$

La fonction de répartition est donc :

$\displaystyle F(\theta )=1-\cos ^{n+1}\theta$

On peut maintenant déterminer $\theta$ et $\phi$ en fonction de 2 variables aléatoires X et Y chacune repartie uniformément sur l'intervalle [0,1] :

$\displaystyle \theta =\arccos((1-X)^{\frac {1}{n+1}})$ ou $\theta =\arccos(X^{\frac {1}{n+1}})$

$\displaystyle \phi =2\pi Y$

Pour n = 0, on obtient une répartition uniforme (équiprobable dans toutes les directions) et au fur et à mesure que n augmente, les directions générées se rapprocheront de la normale. Pour les surfaces lambertiennes diffusant la lumière selon la loi du cosinus, on utilisera n = 1 (cas le plus courant). On rencontre parfois dans la littérature cette formule écrite sous la forme (pour n = 1) : $\theta =\arcsin({\sqrt {X}})$ , ceci est du fait que $F(\theta )=1-\cos ^{2}\theta =\sin ^{2}\theta$ .

Note: Il est également possible de simuler des miroirs plans ou curvilignes à l'aide de cette méthode, la réflexion est alors dépendante de l'angle d'incidence contrairement à la diffusion.

L'utilisation d'un générateur aléatoire type Mersenne Twister est de rigueur.

Coefficients angulaires[modifier | modifier le code]

2 éléments de surface orientés arbitrairement

La méthode par le calcul des coefficients angulaires est moins intuitive que la méthode présentée ci-dessus. L'idée de base est de pré-calculer l'ensemble des relations qui existent entre les N éléments de surface. On peut en déduire une matrice carrée (NxN) représentant l'ensemble de ces relations ainsi qu'une relation de récurrence qui nous permettra de résoudre l'illumination. Le problème évident étant la taille de cette matrice. La technique des hémicubes est dérivée de cette méthode.

L'équation régissant « le flux d'énergie » entre 2 éléments de surface infinitésimaux est donnée par la loi du cosinus et peut être écrite sous forme différentielle de la manière suivante :

$\displaystyle d\gamma _{(dF1\leftarrow dF2)}={\frac {\cos \theta _{1}\cos \theta _{2}}{\Pi r^{2}}}dF_{1}$

Si les éléments de surface sont suffisamment petits, on peut faire l'approximation suivante :

$\displaystyle P_{i}=\sum _{j=1}^{N}{\frac {\cos \theta _{i}\cos \theta _{j}}{\Pi r^{2}}}A_{i}P_{j}$ où $P_{i}$ représente le nombre de photons reçus par l'élément i.

La normalisation $D_{i}=P_{i}/A_{i}$ donne :

$\displaystyle D_{i}=\sum _{j=1}^{N}{\frac {\cos \theta _{i}\cos \theta _{j}}{\Pi r^{2}}}A_{j}D_{j}$ où $D_{i}$ représente la densité sur l'élément i (en nombre de photons par unité de surface)

On pose :

$\displaystyle C_{ij}={\frac {\cos \theta _{i}\cos \theta _{j}}{\Pi r^{2}}}A_{j}$

ou C est une matrice carrée NxN et $A_{j}$ l'aire de l'élément j, s'il y a un obstacle entre deux éléments, qu'il ne se voit pas ou que i=j alors le $C_{ij}$ correspondant est égal à 0. On appelle la matrice C, la matrice des coefficients angulaires.

On définit ensuite un vecteur de N éléments noté D dont la i^e coordonnée représente la densité accumulée par l'élément i. On initialise $D_{i}^{(0)}$ avec $1$ si l'élément i appartient à la source sinon 0. On définit un autre vecteur E (émission intrinsèque) que l'on initialise de la même manière. L'itération suivante converge vers la solution, chaque itération représentant un « rebond global », n est le nombre de rebonds :

$\displaystyle D_{i}^{(n+1)}=\sum _{j=1}^{N}C_{ij}D_{j}^{(n)}+E_{i}$

Tel quel, cet algorithme simule des surfaces lambertiennes non absorbantes (blanche comme le vase) et une source en cosinus comme sur l'image rendue par le Monte Carlo, il est possible d'intégrer l'absorption en corrigeant proportionnellement $C_{ij}$ (voir ci-dessous) ainsi que les sources en puissance de cosinus. Il est préférable pour cela de « découper » l'itération en deux, une pour les surfaces qui diffusent et une pour les sources.

Pour la réflectivité, on définit un vecteur $\rho$ tel que : $\rho _{i}$ = 0 si l'élément i absorbe la totalité de l'énergie (surface noire), 1 si la surface diffuse toute l'énergie reçue (surface blanche), l'équation devient alors :

$\displaystyle D_{i}^{(n+1)}=\rho _{i}\sum _{j=1}^{N}C_{ij}D_{j}^{(n)}+E_{i}\ \$

Note: Cette itération revient à résoudre le système linéaire $\displaystyle D_{i}=\rho _{i}\sum _{j=1}^{N}C_{ij}D_{j}+E_{i}$ en utilisant la méthode de Jacobi

Hémicubes[modifier | modifier le code]

De façon à réduire la taille de la matrice et à permettre un calcul plus rapide de la quantité d'énergie qui est rayonnée d'un polygone sur un élément de surface (Ai), il est possible de projeter ce polygone sur un hémicube, il suffit ensuite de sommer les coefficients angulaires des hemisamples recouverts et on obtient le «facteur de forme» mais on introduit une erreur (surface verte), de plus selon la géométrie, dans certains cas, il se peut que le calcul soit plus long que la méthode simple par maillage du polygone.

Avantages et inconvénients[modifier | modifier le code]

Cette section a besoin d'être recyclée (22 mars 2020).
Une réorganisation et une clarification du contenu sont nécessaires.

	Monte Carlo	Coefficients angulaires	Hémicubes
Mémoire	Faible	Énorme	Raisonnable
Vitesse	Lente	Lente pour le calcul de la matrice puis rapide	Lente pour le calcul de la matrice puis très rapide
Précision	Excellente	Excellente	Moyenne
Maillage adaptatif	Possible (Intérêt limité)	Possible	Possible
Source et réflectivité variable	Pas d'optimisation possible	Immédiat	Immédiat
Géométrie variable	Pas d'optimisation possible	Possibilité de recalculer seulement un sous ensemble de coefficient	Possibilité de recalculer seulement un sous ensemble de coefficient
Parallélisation	Facile et efficace	Moyennement difficile (Efficace en CUDA pour l'itération)	Moyennement difficile (Efficace en CUDA pour l'itération)
Surfaces curvilignes analytiques	Facile	Impossible (Obligation de mailler)	Impossible (Obligation de mailler)
Surfaces/Sources non lambertiennes	Facile	Difficile	Très difficile (voire impossible)
Miroir	Facile	Post processing uniquement *	Post processing uniquement *
Effets atmosphériques	Facile	Difficile (Post)	Difficile et plutôt imprécis (Post)
Réfraction	Facile	Très difficile et en Post	Sans commentaire
Diffraction	Jouable	Pour ceux qui aiment la grande difficulté	Sans commentaire