Tri rapide

Quicksort en action sur une liste de nombres aléatoires. Les lignes horizontales sont les valeurs des pivots.

Découvreur ou inventeur	Charles Antony Richard Hoare^[1]
Date de découverte	1961^[1]
Problèmes liés	Tri par comparaison, diviser pour régner, algorithme de tri
Structure des données	liste ou tableau

Complexité en temps
Pire cas	$O(n^{2})$ ^[2]
Moyenne	$O(n\log n)$ ^[2]
Meilleur cas	$O(n\log n)$ ^[2]

Complexité en espace
Pire cas	$O(n)$
Moyenne	$O(\log n)$

En informatique, le tri rapide ou tri pivot (en anglais quicksort) est un algorithme de tri inventé par C.A.R. Hoare en 1961^[3] et fondé sur la méthode de conception diviser pour régner. Il est généralement utilisé sur des tableaux, mais peut aussi être adapté aux listes. Dans le cas des tableaux, c'est un tri en place mais non stable.

La complexité moyenne du tri rapide pour n éléments est proportionnelle à n log n, ce qui est optimal pour un tri par comparaison, mais la complexité dans le pire des cas est quadratique. Malgré ce désavantage théorique, c'est en pratique un des tris les plus rapides, et donc un des plus utilisés. Le pire des cas est en effet peu probable lorsque l'algorithme est correctement mis en œuvre et il est possible de s'en prémunir définitivement avec la variante Introsort.

Le tri rapide ne peut cependant pas tirer avantage du fait que l'entrée est déjà presque triée. Dans ce cas particulier, il est plus avantageux d'utiliser le tri par insertion ou l'algorithme smoothsort.

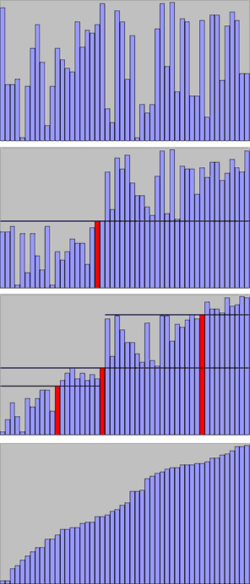
Histoire[modifier | modifier le code]

Le tri rapide est créé en 1960 par Tony Hoare, alors étudiant en visite à l'université d'État de Moscou, lors d'une étude sur la traduction automatique pour le National Physical Laboratory. Il a alors besoin de l'algorithme pour trier les mots devant être traduits, afin de les faire correspondre à un dictionnaire russe-anglais déjà existant, stocké sur une bande magnétique^[4].

« J'ai écrit la procédure immodestement appelée QUICKSORT, sur laquelle s'est construite ma carrière d'informaticien. Sans aucun doute, il faut attribuer cela au génie des concepteurs d'Algol 60 qui ont inclus la récursivité dans leur langage et m'ont permis de décrire mon invention si élégamment pour le monde entier. Je considère que c'est l'un des objectifs primordiaux des langages de programmation que de permettre d'exprimer élégamment des bonnes idées. »

C. A. R. Hoare, « The emperor's old clothes », Communications of the ACM, vol. 24, n^o 2,‎ février 1981, p. 5–83 (DOI 10.1145/358549.358561, lire en ligne [PDF])

Description de l'algorithme[modifier | modifier le code]

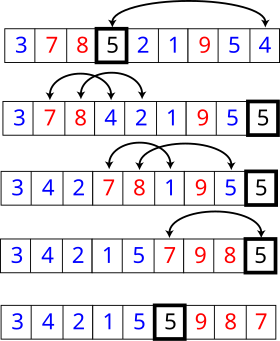
La méthode consiste à placer un élément du tableau (appelé pivot) à sa place définitive, en permutant tous les éléments de telle sorte que tous ceux qui sont inférieurs au pivot soient à sa gauche et que tous ceux qui sont supérieurs au pivot soient à sa droite.

Cette opération s'appelle le partitionnement. Pour chacun des sous-tableaux, on définit un nouveau pivot et on répète l'opération de partitionnement. Ce processus est répété récursivement, jusqu'à ce que l'ensemble des éléments soit trié.

Concrètement, pour partitionner un sous-tableau :

le pivot est placé à la fin (arbitrairement), en l'échangeant avec le dernier élément du sous-tableau ;
tous les éléments inférieurs au pivot sont placés en début du sous-tableau ;
le pivot est déplacé à la fin des éléments déplacés.

partitionner(tableau T, entier premier, entier dernier, entier pivot)
    échanger T[pivot] et T[dernier]  // échange le pivot avec le dernier du tableau , le pivot devient le dernier du tableau
    j := premier
    pour i de premier à dernier - 1 // la boucle se termine quand i = (dernier élément du tableau).
        si T[i] <= T[dernier] alors
            échanger T[i] et T[j]
            j := j + 1
    échanger T[dernier] et T[j]
    renvoyer j

tri_rapide(tableau T, entier premier, entier dernier)
        si premier < dernier alors
            pivot := choix_pivot(T, premier, dernier)
            pivot := partitionner(T, premier, dernier, pivot)
            tri_rapide(T, premier, pivot-1)
            tri_rapide(T, pivot+1, dernier)

Choisir un pivot aléatoirement dans l'intervalle [premier, dernier] garantit l'efficacité de l'algorithme, mais il existe d'autres possibilités (voir la section « Choix du pivot et complexité »).

Le partitionnement peut être fait en temps linéaire, en place. La mise en œuvre la plus simple consiste à parcourir le tableau du premier au dernier élément, en formant la partition au fur et à mesure : à la i-ème étape de l'algorithme ci-dessous, les éléments $T[0],\cdots ,T[j-1]$ sont inférieurs au pivot, tandis que $T[j],\cdots ,T[i-1]$ sont supérieurs au pivot.

Cet algorithme de partitionnement rend le tri rapide non stable : il ne préserve pas nécessairement l'ordre des éléments possédant une clef de tri identique. On peut résoudre ce problème en ajoutant l'information sur la position de départ à chaque élément et en ajoutant un test sur la position en cas d'égalité sur la clef de tri.

Le partitionnement peut poser problème si les éléments du tableau ne sont pas distincts. Dans le cas le plus dégénéré, c'est-à-dire un tableau de $n$ éléments égaux, cette version de l'algorithme a une complexité quadratique. Plusieurs solutions sont possibles : par exemple se ramener au cas d'éléments distincts en utilisant la méthode décrite pour rendre le tri stable, ou bien utiliser un autre algorithme (voir la section « Algorithme de partitionnement alternatif »).

Choix du pivot et complexité[modifier | modifier le code]

Pivot arbitraire[modifier | modifier le code]

Une manière simple de choisir le pivot est de prendre toujours le premier élément du sous-tableau courant (ou le dernier). Lorsque toutes les permutations possibles des entrées sont équiprobables, la complexité moyenne du tri rapide en sélectionnant le pivot de cette façon est Θ(n log n). Cependant, la complexité dans le pire des cas est Θ(n²), et celle-ci est atteinte lorsque l'entrée est déjà triée ou presque triée^[5].

Si on prend comme pivot le milieu du tableau, le résultat est identique, bien que les entrées problématiques soient différentes.

Il est possible d'appliquer une permutation aléatoire au tableau pour éviter que l'algorithme soit systématiquement lent sur certaines entrées. Cependant, cette technique est généralement moins efficace que de choisir le pivot aléatoirement.

Pivot aléatoire[modifier | modifier le code]

Si on utilise la méthode donnée dans la description de l'algorithme, c'est-à-dire choisir le pivot aléatoirement de manière uniforme parmi tous les éléments, alors la complexité moyenne du tri rapide est Θ(n log n) sur n'importe quelle entrée. Dans le pire des cas, la complexité est Θ(n²). Néanmoins, l'écart type de la complexité est seulement Θ(n), ce qui signifie que l'algorithme s'écarte peu du temps d'exécution moyen^[6].

Dans le cas le meilleur, l'algorithme est en Θ(n log n).

Calcul de la complexité[modifier | modifier le code]

On donne une preuve de la complexité temporelle moyenne du tri rapide d'un tableau de taille $n$ ^[5].

On note $z_{1},\dots ,z_{n}$ les éléments du tableau donnés par ordre croissant. Pour $i<j$ on note $Z_{ij}=\{z_{i},z_{i+1},\dots ,z_{j}\}$ . Initialement, le tableau à trier est $z_{\sigma (1)},\dots ,z_{\sigma (n)}$ où $\sigma$ est une permutation des entiers compris entre 1 et $n$ .

Les opérations à effectuer sont les choix de pivot et les comparaisons qui ont lieu lors des partitions autour de chaque pivot. Dès lors qu'un pivot est choisi il n'est plus impliqué dans les partitions qui suivent et donc une exécution de l'algorithme fait intervenir au plus $n$ choix de pivot, et chaque choix se fait en temps constant. De plus tout élément est comparé à un élément au plus une fois, car tout élément n'est comparé qu'à un pivot, et une fois effectuée la partition autour d'un pivot donné, celui-ci n'intervient plus dans l'exécution de l'algorithme une fois la partition finie. En notant $X$ le nombre total de comparaison on obtient que la complexité d'une exécution est donc $O(X+n)$ . De plus si l'on note $X_{ij}$ la variable aléatoire qui vaut 1 si $z_{i}$ est comparé à $z_{j}$ et 0 sinon, on déduit que l'on a pour une exécution donnée $X=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}X_{ij}$ . On cherche à calculer ${\mathtt {E}}[X]$ l'espérance de $X$ . C'est-à-dire ${\mathtt {E}}[X]=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}\mathbb {P} \{{\text{L'algorithme compare }}z_{i}{\text{et }}z_{j}\}$ .

Or $z_{i}$ est comparé à $z_{j}$ si et seulement si le premier élément de $Z_{ij}$ à être choisi comme pivot est soit $z_{i}$ soit $z_{j}$ . En effet si c'est un autre élément qui est choisi en premier comme pivot, alors $z_{i}$ et $z_{j}$ sont envoyés dans deux sous-tableaux différents de la partition, et les comparaisons sont effectuées exclusivement entre éléments d'un même sous-tableau. De plus la probabilité que le premier élément de $Z_{ij}$ à être choisi comme pivot soit $z_{i}$ ou $z_{j}$ vaut ${\frac {2}{j-i+1}}$ car les choix de pivot sont équiprobables et mutuellement exclusifs, et car $Z_{ij}$ contient $j-i+1$ éléments.

On a donc ${\mathtt {E}}[X]=\sum _{i=1}^{n-1}\sum _{j=i+1}^{n}{\frac {2}{j-i+1}}=\sum _{i=1}^{n-1}\sum _{k=1}^{n-i}{\frac {2}{k+1}}$ .

Or $\sum _{k=1}^{n-i}{\frac {2}{k+1}}\leq \sum _{k=1}^{n}{\frac {2}{k}}=O(\log(n))$ (c'est une propriété de la série harmonique).

Par conséquent ${\mathtt {E}}[X]=\sum _{i=1}^{n-1}O(\log(n))=O(n\log(n))$ .

La complexité moyenne du tri rapide lorsque le pivot est choisi aléatoirement est donc $O(n\log(n))$ .

Pivot optimal[modifier | modifier le code]

En théorie, on pourrait faire en sorte que la complexité de l'algorithme soit Θ(n log n) dans le pire cas en prenant comme pivot la valeur médiane du sous-tableau. En effet, dans ce cas l'arbre des appels récursifs de l'algorithme a une hauteur égale à ${\mathtt {log}}_{2}(n)$ et chacun de ses étages a la complexité $\theta (n)$ . L'algorithme BFPRT ou médiane des médianes permet en effet de calculer cette médiane de façon déterministe en temps linéaire^[7].

Mais l'algorithme n'est pas suffisamment efficace dans la pratique, et cette variante est peu utilisée.

Variantes et optimisations[modifier | modifier le code]

Algorithme de partitionnement alternatif[modifier | modifier le code]

Il existe un algorithme de partitionnement plus complexe, qui réduit le nombre d'échanges effectués lors du partitionnement. De plus, les éléments égaux au pivot sont mieux répartis des deux côtés de celui-ci qu'avec l'algorithme précédent. Ainsi, l'algorithme reste en Θ(n log n) même sur un tableau dont tous les éléments sont identiques.

Le principe de l'algorithme est le suivant :

Trouver le plus petit i tel que T[i] soit supérieur ou égal au pivot.
Trouver le plus grand j tel que T[j] soit inférieur ou égal au pivot.
Si i<j, échanger T[i] et T[j] puis recommencer.

Il est possible de formaliser cet algorithme de sorte qu'il soit linéaire :

partitionner(tableau T, premier, dernier, pivot)
    échanger T[pivot] et T[premier]
    i = premier + 1, j = dernier
    tant que i < j
        tant que i < j et T[i] < T[premier], faire i := i + 1
        tant que i < j et T[j] > T[premier], faire j := j - 1
        échanger T[i] et T[j]
        i := i + 1, j := j - 1
    fin tant que
    ''// le tableau est à présent en 3 parties consécutives : pivot, partie gauche, partie droite''
    ''// dans partie gauche, tous les éléments sont <= pivot''
    ''// dans partie droite, tous les éléments sont >= pivot''
    ''// mais les deux parties peuvent se chevaucher : i-j peut être 0, 1 ou 2''
    ''// il faut replacer le pivot entre les 2 parties et retourner l'indice du pivot : c'est assez compliqué...''
    ''// il vaut mieux laisser le pivot à sa place au départ et le déplacer en cas de chevauchement :''

Combinaison avec d'autres algorithmes de tri[modifier | modifier le code]

Traitement spécial des petits sous-problèmes[modifier | modifier le code]

Une optimisation utile consiste à changer d'algorithme lorsque le sous-ensemble de données non encore trié devient petit. La taille optimale des sous-listes dépend du matériel et des logiciels utilisés, mais est de l'ordre de 15 éléments. On peut alors utiliser le tri par sélection ou le tri par insertion. Le tri par sélection ne sera sûrement pas efficace pour un grand nombre de données, mais il est souvent plus rapide que le tri rapide sur des listes courtes, du fait de sa plus grande simplicité.

Robert Sedgewick suggère une amélioration (appelée Sedgesort) lorsqu'on utilise un tri simplifié pour les petites sous-listes^[8] : on peut diminuer le nombre d'opérations nécessaires en différant le tri des petites sous-listes après la fin du tri rapide, après quoi on exécute un tri par insertion sur le tableau entier.

LaMarca et Ladner ont étudié « l'influence des caches sur les performances des tris »^[9], un problème prépondérant sur les architectures récentes dotées de hiérarchies de caches avec des temps de latence élevés lors des échecs de recherche de données dans les caches. Ils concluent que, bien que l'optimisation de Sedgewick diminue le nombre d'instructions exécutées, elle diminue aussi le taux de succès des caches à cause de la plus large dispersion des accès à la mémoire (lorsque l'on fait le tri par insertion à la fin sur tout le tableau et non au fur et à mesure), ce qui entraîne une dégradation des performances du tri. Toutefois l'effet n'est pas dramatique et ne devient significatif qu'avec des tableaux de plus de 4 millions d'éléments de 64 bits. Cette étude est citée par Musser.

Introsort[modifier | modifier le code]

Article détaillé : Introsort.

Une variante du tri rapide devenue largement utilisée^{[réf. nécessaire]} est introsort alias introspective sort^[10]. Elle démarre avec un tri rapide puis utilise un tri par tas lorsque la profondeur de récursivité dépasse une certaine limite prédéfinie. Ainsi, sa complexité dans le cas le pire est Θ(n log n).

Espace mémoire[modifier | modifier le code]

Une mise en œuvre naïve du tri rapide utilise un espace mémoire proportionnel à la taille du tableau dans le pire des cas. Il est possible de limiter la quantité de mémoire à Θ(log n) dans tous les cas en faisant le premier appel récursif sur la liste la plus petite. Le second appel récursif, situé à la fin de la procédure, est récursif terminal. Il peut donc être transformé en itération de la manière suivante :

tri_rapide(T, gauche, droite)
    tant que droite-gauche+1 > 1
        sélectionner un pivot T[pivotIndex]
        pivotNewIndex := partition(T, gauche, droit, pivotIndex)
        si pivotNewIndex-1 - gauche < droit - (pivotNewIndex+1)
            tri_rapide(T, gauche, pivotNewIndex-1)
            gauche := pivotNewIndex+1
        sinon
            tri_rapide(T, pivotNewIndex+1, droit)
            droit := pivotNewIndex-1
        fin_si
   fin_tant_que

Variante pour la sélection d'élément[modifier | modifier le code]

Un algorithme inspiré du tri rapide appelé Quickselect, fonctionnant en temps linéaire en moyenne, permet de déterminer le k-ème plus petit élément dans un tableau. Un cas particulier notable est k=n/2, qui correspond à la recherche de la médiane.

Le principe de l'algorithme Quickselect est le suivant : à chaque étape, on réalise une partition selon un pivot choisi aléatoirement. Une fois la partition effectuée, il est possible de savoir de quel côté de la partition se trouve le k-ème élément (ou bien si c'est le pivot lui-même). Dans le cas où le pivot n'est pas le k-ème élément, on appelle récursivement l'algorithme, mais seulement du côté où se trouve l'élément. À la fin de l'algorithme, le k-ème élément du tableau est alors le k-ème plus petit élément du tableau.

Voir aussi[modifier | modifier le code]

Sur les autres projets Wikimedia :

Implémentations du tri rapide, sur Wikibooks

Articles connexes[modifier | modifier le code]

Loi de Bernoulli, en particulier la section « Coût moyen de l'algorithme de tri rapide ».
Quickselect, l'algorithme de sélection associé à Quicksort.

Liens externes[modifier | modifier le code]

Références[modifier | modifier le code]

↑ ^{a et b} (en) C. A. R. Hoare, « Algorithm 64: Quicksort », Communications of the ACM, New York, ACM, vol. 4, n^o 7,‎ 1^er juillet 1961, p. 321 (ISSN 0001-0782 et 1557-7317, OCLC 1514517, DOI 10.1145/366622.366644)
↑ ^{a b et c} « https://www.khanacademy.org/computing/computer-science/algorithms/quick-sort/a/analysis-of-quicksort » (consulté le 9 mars 2017)
↑ Hoare, C. A. R. « Partition: Algorithm 63, » « Quicksort: Algorithm 64, » and « Find: Algorithm 65. » Comm. ACM 4, 321-322, 1961.
↑ (en) « An Interview with C.A.R. Hoare », Communications of the ACM, March 2009 ("premium content").
↑ ^{a et b} (en) Thomas H. Cormen, Charles E. Leiserson et Ronald L. Rivest, Introduction à l'algorithmique, Paris, Dunod, 2002, xxix+1146 (ISBN 978-2-10-003922-7, SUDOC 068254024), chap. 7 (« Tri rapide »)
↑ Donald E. Knuth, The Art of Computer Programming, Volume 3: Sorting and Searching, Addison-Wesley 1973, (ISBN 0-201-03803-X) (section 5.2.2, p. 121).
↑ (en) Thomas H. Cormen, Charles E. Leiserson et Ronald L. Rivest, Introduction à l'algorithmique, Paris, Dunod, 2002, xxix+1146 (ISBN 978-2-10-003922-7, SUDOC 068254024), chap. 9 (« Médians et rangs »).
↑ R. Sedgewick. Implementing quicksort programs, Communications of the ACM, 21(10):847857, 1978.
↑ A. LaMarca et Richard E. Ladner, « The Influence of Caches on the Performance of Sorting » Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, 1997, p. 370-379.
↑ David Musser. Introspective Sorting and Selection Algorithms, Software Practice and Experience vol 27, number 8, pages 983-993, 1997.

[wikidata-902700ebb24fee7097cfa0aa877efab199ae4eb4Q55952563-1] {a et b} (en) C. A. R. Hoare, « Algorithm 64: Quicksort », Communications of the ACM, New York, ACM, vol. 4, n^o 7,‎ 1^er juillet 1961, p. 321 (ISSN 0001-0782 et 1557-7317, OCLC 1514517, DOI 10.1145/366622.366644)

[wikidata-6ba7c77af82618ecac179a5d4db7f8c913cda63c-2] {a b et c} « https://www.khanacademy.org/computing/computer-science/algorithms/quick-sort/a/analysis-of-quicksort » (consulté le 9 mars 2017)

[3] Hoare, C. A. R. « Partition: Algorithm 63, » « Quicksort: Algorithm 64, » and « Find: Algorithm 65. » Comm. ACM 4, 321-322, 1961.

[4] (en) « An Interview with C.A.R. Hoare », Communications of the ACM, March 2009 ("premium content").

[Cormen7-5] {a et b} (en) Thomas H. Cormen, Charles E. Leiserson et Ronald L. Rivest, Introduction à l'algorithmique, Paris, Dunod, 2002, xxix+1146 (ISBN 978-2-10-003922-7, SUDOC 068254024), chap. 7 (« Tri rapide »)

[6] Donald E. Knuth, The Art of Computer Programming, Volume 3: Sorting and Searching, Addison-Wesley 1973, (ISBN 0-201-03803-X) (section 5.2.2, p. 121).

[Cormen-7] (en) Thomas H. Cormen, Charles E. Leiserson et Ronald L. Rivest, Introduction à l'algorithmique, Paris, Dunod, 2002, xxix+1146 (ISBN 978-2-10-003922-7, SUDOC 068254024), chap. 9 (« Médians et rangs »).

[8] R. Sedgewick. Implementing quicksort programs, Communications of the ACM, 21(10):847857, 1978.

[9] A. LaMarca et Richard E. Ladner, « The Influence of Caches on the Performance of Sorting » Proceedings of the Eighth Annual ACM-SIAM Symposium on Discrete Algorithms, 1997, p. 370-379.

[10] David Musser. Introspective Sorting and Selection Algorithms, Software Practice and Experience vol 27, number 8, pages 983-993, 1997.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]