Principe d'inclusion-exclusion
En combinatoire, le principe d’inclusion-exclusion permet d’exprimer le nombre d’éléments (ou cardinal) d'une réunion finie d'ensembles finis en fonction du nombre d'éléments de ces ensembles et de leurs intersections. Il se généralise en termes de probabilités.
Il est attribué au mathématicien Abraham de Moivre, et connu également (lui ou sa version probabiliste) sous le nom de formule du crible de Poincaré, formule de Poincaré, ou formule du crible.
Le cas de deux ensembles[modifier | modifier le code]
Exemple[modifier | modifier le code]
Parmi 20 étudiants, 10 étudient les mathématiques, 11 étudient la physique, et 4 étudient les deux. Combien y a-t-il d’étudiants qui n’étudient ni les mathématiques ni la physique ?
La construction d'un diagramme de Venn permet de visualiser simplement la répartition générale des étudiants.
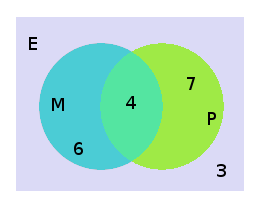
Une zone de couleur représente un groupe. E représente le groupe entier d’étudiants, M représente ceux qui ont la propriété d'« étudier les mathématiques », P représente ceux qui possèdent la propriété d'« étudier la physique ».
On note ensuite pour chaque zone le nombre d’étudiants. Étant donné que quatre personnes étudient à la fois les mathématiques et la physique, l’intersection des deux cercles compte 4 étudiants. Il reste donc 10 – 4 = 6 personnes qui étudient les mathématiques mais pas la physique et 11 – 4 = 7 personnes qui étudient la physique mais pas les mathématiques. Par suite, il reste donc 20 – (6 + 4 + 7) = 3 personnes qui n’étudient ni les mathématiques, ni la physique.
Ce résultat se retrouve facilement en utilisant le principe d’inclusion-exclusion qui donne le nombre d’étudiants ne possédant pas ces deux propriétés : 20 – 10 – 11 + 4 = 3.
Formule pour n = 2[modifier | modifier le code]
Soient A et B deux ensembles finis, la formule s'écrit
où |A| et |B| représentent les cardinaux respectifs de A et B.
En d’autres termes, nous pouvons compter les éléments de la réunion de deux ensembles A et B en additionnant les cardinaux de ces deux ensembles et en soustrayant le cardinal de leur intersection.
Cas général[modifier | modifier le code]
Soient A1, ..., An n ensembles finis. Nous avons
où |A| désigne le cardinal d'un ensemble fini A.
Cette formule peut aussi s'écrire de façon plus condensée :
Théorème — .
Elle peut se démontrer par récurrence sur n, ou en utilisant les fonctions indicatrices[1].
Le terme , somme des cardinaux des intersections k à k des , possède termes.
Si donc les intersections k à k des ont toutes le même nombre d'éléments , la formule de Poincaré s'écrit .
Soit E un ensemble fini, contenant les ensembles Ai. On déduit, par passage au complémentaire, le cardinal de l'ensemble des éléments de E qui n'appartiennent à aucun des Ai :
- .
Le principe d’inclusion-exclusion peut être vu comme un cas particulier d'une généralisation de la formule d'inversion de Möbius.
Version probabiliste[modifier | modifier le code]
Soient un espace probabilisé et éléments de la tribu . Nous avons
- .
Cette formule peut se démontrer par récurrence sur n, ou en utilisant des fonctions indicatrices, de la même manière que la formule précédente. On peut aussi la formuler de la manière suivante :
- .
Applications[modifier | modifier le code]
Inégalités de Bonferroni[modifier | modifier le code]
Les sommes partielles des premiers termes de la formule fournissent alternativement un majorant et un minorant de la somme complète, et peuvent être utilisées comme approximations de celle-ci : ces majorations et minorations sont appelées les inégalités de Bonferroni, du nom de leur auteur, Carlo Emilio Bonferroni.
Dérangements et nombre de points fixes d'une permutation[modifier | modifier le code]
En combinatoire, la formule du crible permet de déterminer le nombre de dérangements d'un ensemble fini, et donc de résoudre le problème des rencontres. Un dérangement d'un ensemble X est une bijection de X sur lui-même sans point fixe. Grâce au principe d'inclusion-exclusion, et en prenant pour Ai l'ensemble des permutations de X laissant i invariant, on peut prouver[1] que si le cardinal de X est égal à n, alors le nombre de dérangements de X est égal à . C'est l'entier le plus proche de n!/e (où e désigne la base des logarithmes népériens). Il s'ensuit que la probabilité pour qu'une bijection prise au hasard[2] soit un dérangement tend rapidement vers 1/e lorsque n tend vers l'infini.
On peut pousser plus loin l'étude statistique des points fixes des permutations. Notons N(ω) le nombre de points fixes d'une permutation ω. Ce nombre est nul si et seulement si ω est un dérangement. En cela, la proposition suivante précise le résultat concernant les dérangements (qui n'est autre que le calcul de ) :
Proposition[1] — Pour tout entier k compris entre 0 et n,
En particulier, la loi de N est très proche de la loi de Poisson de paramètre 1, pour n grand. Cela illustre le paradigme de Poisson, selon lequel une somme d'un grand nombre de variables de Bernoulli de petit paramètre, peu corrélées, suit approximativement la loi de Poisson : N peut être vue comme une telle somme. Cette écriture permet de calculer l'espérance et la variance de N plus rapidement qu'à partir de l'expression ci-dessus de la loi de N.
Le principe d'inclusion-exclusion permet aussi de montrer[3], en prenant pour Aτ l'ensemble des permutations de X admettant un cycle τ d'ordre 2, que le nombre de permutations n'ayant pas de cycle d'ordre 2 est , où m est la partie entière de n/2. Plus généralement, le nombre de permutations n'ayant pas de cycle d'ordre p est , où m est la partie entière de n/p.
Nombre de surjections d'un ensemble fini dans un autre[modifier | modifier le code]
Soient X et Y deux ensembles finis. Considérons l'ensemble des applications de X dans Y et, pour tout élément y de Y, le sous-ensemble des applications qui ne prennent jamais la valeur y. L'ensemble des surjections de X dans Y est alors égal à et son cardinal vaut donc :
ou encore, par changement d'indice :
Proposition[1] — Soient . Le nombre de surjections d'un ensemble à éléments dans un ensemble à éléments est donné par :
Nombres de Worpitzky[modifier | modifier le code]
Soit m et n deux entiers strictement positifs. Le nombre de Wortpitzky[4] est le nombre de façon de colorier m carrés disposés en ligne avec n couleurs, chaque couleur apparaissant au moins une fois, et chaque carré pouvant aussi rester incolore. On peut trouver une expression de en utilisant la version probabiliste du principe d'inclusion-exclusion. Pour chaque carré, on tire une couleur au hasard parmi {1, ..., n+1} avec une loi uniforme. Si la couleur tirée est n+1, cela signifie que le carré est incolore. Pour chaque couleur i variant de 1 à n, on note l'événement : la couleur i n'est utilisée dans aucun carré. On a alors :
- pour tout i < j.
- pour tout i < j < k
etc. La formule d'inclusion-exclusion donne :
La probabilité de l'événement contraire n'est autre que , d'où, finalement :
Notes et références[modifier | modifier le code]
- Voir le lien ci-dessous vers Wikiversité.
- L'espace probabilisé est ici l'ensemble fini des permutations de , muni de la tribu triviale et de la loi uniforme.
- (en) Larry Carter et Stan Wagon, « The mensa correctionnal institute », Amer. Math. Monthly, vol. 125, no 4, , p. 306-319.
- Sam Vandervelde, « The Worpitzky numbers revisited », Amer. Math. Monthly, vol. 125, no 3,















![{\displaystyle \mathbb {P} \left(\,\bigcup _{i=1}^{n}A_{i}\,\right)=\sum _{S\subset [\![1,n]\!],\,S\neq \varnothing }(-1)^{|S|-1}\ \mathbb {P} \left(\bigcap _{i\in S}\,A_{i}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/846f199cfb3a5cc0416bc5ac14f6d8a434d1b2a2)






















![{\displaystyle [\![1,n]\!]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9742260f2c04dfe897a9b8702005a64dcc12a34)