Problème du cavalier

Le problème du cavalier (ou encore polygraphie ou algorithme du cavalier ou cavalier d'Euler) est un problème mathématico-logique fondé sur les déplacements du cavalier du jeu d'échecs : un cavalier partant d'une case quelconque doit visiter chaque case sans y repasser.

Variantes[modifier | modifier le code]

Selon les pièces[modifier | modifier le code]

Si le but est généralement de parcourir toutes les cases du plateau avec un cavalier, une variante a été étudiée au Moyen-Orient médiéval où la pièce alterne entre un mouvement de cavalier et un mouvement en diagonale (voir infra).

Selon les formes de plateau[modifier | modifier le code]

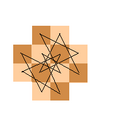
Le problème a initialement porté sur le parcours d'un échiquier carré de 64 cases ou sur un demi-échiquier de 32 cases ; mais il a par la suite été étudié pour d'autres dimensions et également pour des formes non-rectangulaires, dont des croix.

Selon les parcours[modifier | modifier le code]

Le parcours peut être ouvert ou se refermer sur lui-même, auquel cas on parle de tour du cavalier. On peut aussi chercher des solutions avec des symétries particulières ou encore les plus longues solutions sans croisement^[1].

Circuit du cavalier sur un échiquier de taille 24 × 24 obtenu par un réseau de neurones.
Parcours ouvert sur un échiquier de taille 130 x 130 obtenu en utilisant l'heuristique de Warnsdorf.
Parcours ouvert sur un échiquier de taille 5 x 5.
Tour de cavalier sur un plateau en forme de croix.
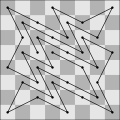
Circuit fermé sans croisement maximal sur un échiquier de taille 49 ; sa longueur est de 24 sauts.
Parcours ouvert sans croisement maximal sur un échiquier de taille 64 ; sa longueur est de 35 sauts.

Histoire[modifier | modifier le code]

Inde[modifier | modifier le code]

On en trouve la première occurrence dans un traité d'ornement poétique indien, le Kavyalankara du poète Rudrata ^[2].

Une solution au problème du parcours de l'intégralité d'un demi-échiquier de 32 cases a été trouvée dans un manuscrit datant du début du X^e siècle ; cette solution pouvant facilement être adaptée pour obtenir par juxtaposition le parcours complet d'un échiquier de 64 cases^[3]. Cette solution n'est pas un circuit car elle ne permet pas de revenir au point de départ.

Une encyclopédie indienne datant du XVII^e siècle donne un exemple de parcours fermé sur un échiquier de 64 cases^[4]. Charles Monneron rapporte d'Inde une autre solution au problème, qui sera imprimée par la suite dans l'Encyclopédie^[5].

Solution du parcours sur un demi échiquier (900 ap. J.-C.).
1	30	9	20	3	24	11	26
16	19	2	29	10	27	4	23
31	8	17	14	21	6	25	12
18	15	32	7	28	13	22	5

Parcours fermé indien du XVII^e siècle.
2	51	6	15	64	25	28	23
7	14	1	50	5	22	43	26
52	3	8	63	16	27	24	29
9	62	13	4	49	42	21	44
12	53	10	17	36	45	30	41
61	56	59	48	31	40	35	20
58	11	54	37	18	33	46	39
55	60	57	32	47	38	19	34

Parcours ouvert à extrémités accolées rapporté par Monneron.
17	20	39	4	37	22	49	6
40	53	18	21	8	5	36	23
19	16	3	38	61	50	7	48
54	41	52	1	64	9	24	35
15	2	13	60	51	62	47	10
42	55	30	63	12	59	34	25
29	14	57	44	27	32	11	46
56	43	28	31	58	45	26	33

Le rajah Krishnaraja Wadiyar III (en) s'est intéressé au sujet dans la première moitié du XIX^e siècle, on lui doit l'un des premiers parcours de cavalier connus dont la numérotation des cases forme un carré magique^[6].

Monde arabe[modifier | modifier le code]

Circuit fermé[modifier | modifier le code]

Le cavalier d'Euler est connu depuis fort longtemps. Vers 840, le joueur et théoricien d'échecs arabe al-Adli ar-Rumi en donne déjà une solution.

Des moyens mnémotechniques permettant de retenir une solution au circuit du cavalier sont attestés dans un manuscrit copié en 1141, lequel reprend des textes datant au plus du X^e siècle ; il s'agit de poèmes de 64 vers dont chacun est associé aux coordonnées d'une case de l'échiquier^[7]. Quatre tels poèmes sont connus, ce qui permet de conclure que le problème du circuit du cavalier était populaire dans le monde arabo-musulman, et qu'aucune méthode générale de construction d'un tel parcours n'était connue^[8].

Autres règles de parcours[modifier | modifier le code]

Les savants arabes ont également étudié un problème voisin dans lequel la pièce à déplacer adopte alternativement le déplacement du cavalier et celui d'une autre pièce, conseiller ou éléphant, du chatrang (la version des échecs pratiquée dans le monde arabe médiéval). Le conseiller (ancêtre de la dame) et l'éléphant (ancêtre du fou) se déplaçant respectivement d'une case en diagonale et de deux cases en diagonale^[9]. Des poèmes ont également été composés pour en mémoriser des solutions^[5].

Parcours fermé arabe d'un cavalier-éléphant.
49	42	40	51	9	34	36	11
47	52	54	45	39	12	14	33
41	50	48	43	37	10	8	35
55	44	46	53	15	32	38	13
61	22	16	63	5	26	28	7
19	56	58	21	31	64	2	25
17	62	60	23	29	6	4	27
59	20	18	57	3	24	30	1

Parcours fermé arabe d'un cavalier-conseiller.
37	14	16	35	33	18	24	31
15	36	34	17	19	32	30	25
13	38	48	11	21	26	28	23
39	12	10	49	27	20	22	29
9	42	40	47	61	50	52	63
43	8	46	41	51	60	62	53
45	6	4	59	57	2	64	55
7	44	58	5	3	56	54	1

Occident[modifier | modifier le code]

Pendant le Moyen Âge et la Renaissance[modifier | modifier le code]

On trouve dans un manuscrit anglo-normand du XIV^e siècle un parcours ouvert dont le but est d'amener le cavalier d'un coin à un autre^[3]. Plusieurs autres manuscrits plus tardifs donnent également des parcours ouverts sur des échiquiers ou des demi-échiquiers^[10].

Solution datée du XIV^e siècle.
23	26	11	4	49	52	45	40
10	3	22	25	46	41	48	51
27	24	5	12	53	50	39	44
2	9	28	21	42	47	54	59
29	20	13	6	61	58	43	38
8	1	16	19	32	35	60	55
17	30	7	14	57	62	37	34
.	15	18	31	36	33	56	63

Au début du XVIII^e siècle[modifier | modifier le code]

Pierre Rémond de Montmort a étudié ce problème, et en donne une solution citée par Martin Grandin^[11]. Ce dernier reprend également deux autres solutions obtenues par Abraham de Moivre et par de Mairan^[12].

Solution de Rémond de Montmort
58	23	62	15	64	21	54	13
61	16	59	22	55	14	51	20
24	57	10	63	18	49	12	53
9	60	17	56	11	52	19	50
34	25	36	7	40	27	48	5
37	8	33	26	45	6	41	28
32	35	2	39	30	43	4	47
1	38	31	44	3	46	29	42

Solution de de Moivre où le carré central est visité après la bordure.
34	49	22	11	36	39	24	1
21	10	35	50	23	12	37	40
48	33	62	57	38	25	2	13
9	20	51	54	63	60	41	26
32	47	58	61	56	53	14	3
19	8	55	52	59	64	27	42
46	31	6	17	44	29	4	15
7	18	45	30	5	16	43	28

Solution fermée de de Mairan.
56	9	26	43	54	7	32	29
25	44	55	8	27	30	53	6
10	57	24	39	42	33	28	31
23	40	45	36	1	52	5	34
46	11	58	41	38	35	64	51
59	22	37	48	19	2	15	4
12	47	20	61	14	17	50	63
21	60	13	18	49	62	3	16

Les travaux d'Euler[modifier | modifier le code]

Le mathématicien Leonhard Euler reprit l'étude scientifique en 1759. La « Solution d'une question curieuse qui ne paraît soumise à aucune analyse »^[13] n'est cependant publiée qu'en 1766. Côme Alexandre Collini en publia une dans le Journal encyclopédique en 1773.

Euler y montre la solution de plusieurs problèmes^[14]:

comment obtenir un trajet complet à partir d'un trajet partiel ;
comment transformer un trajet ouvert en trajet fermé ;
comment obtenir un trajet symétrique ;
l'obtention de parcours sur des échiquiers carrés ou rectangulaires de taille variable ;
l'obtention de parcours complets sur des échiquiers en forme de croix ou de croix rhombiques.

Une solution publiée par Euler^[13].
Une solution proposée par Euler^[13]. Celle-ci est symétrique par rapport au centre de l'échiquier, et parcourt d'abord la moitié inférieure de ce dernier, puis la partie supérieure.
Solution du tour sur un échiquier 10x10, proposée par Euler^[13].

Euler a également commis des erreurs, il a ainsi affirmé qu'aucun trajet fermé n'est possible sur un échiquier de largeur 3 ; un contre-exemple a été donné en 1917 sur un échiquier de taille 3×10^[15]^,^{[N 1]}.

Parcours fermé sur un échiquier de taille 3×10^[15].
1	28	25	6	19	4	21	10	13	16
26	7	30	3	24	9	18	15	22	11
29	2	27	8	5	20	23	12	17	14

Études ultérieures[modifier | modifier le code]

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Au fil des siècles, les mathématiciens étudient ce thème en variant :

les dimensions de l'échiquier,
le nombre de joueurs,
les propriétés du parcours,
la façon dont un cavalier se déplace.

Il a été proposé d'étudier les parcours du cavalier dans lesquels la somme des numéros de passage d'une case est constante suivant les lignes et les colonnes^{[N 2]}. En 1888, 83 tels parcours (dont 27 fermés) ont été déposés au Conservatoire National des Arts et Métiers ; aucun de ces parcours ne donne un carré magique car la somme n'est pas la même en suivant les diagonales^[16]. Un 84^e parcours a été découvert dans les années 1970^[16]^,^{[N 3]}. Une recherche exhaustive a établi en 2003 que sur un échiquier il existe en tout 108 parcours différents formant des carrés magiques dont aucun n'a de diagonales égales^[6]^,^[17]^,^{[N 4]}.

Parcours fermé qui est aussi un carré magique. (Sauf en ce qui concerne les diagonales)
42	59	2	17	40	15	22	63
3	18	41	60	21	64	39	14
58	43	20	1	16	23	62	37
19	4	57	44	61	38	13	24
56	45	6	29	12	25	36	51
5	30	55	48	33	52	11	26
46	7	32	53	28	9	50	35
31	54	47	8	49	34	27	10

Parcours fermé sur 12 × 12 cases qui est aussi un carré magique. (Y compris en ce qui concerne les diagonales)^[18]^,^[19]
1	70	107	112	5	66	103	116	9	64	99	118
108	111	2	69	104	115	6	65	100	117	10	63
71	106	109	4	113	102	67	8	61	98	119	12
110	3	72	105	68	7	114	101	120	11	62	97
73	142	35	40	77	140	17	60	93	122	13	58
36	39	74	141	32	41	92	121	16	59	96	123
143	34	37	76	139	78	55	18	125	94	57	14
38	75	144	33	42	31	126	91	56	15	124	95
81	136	29	44	79	138	19	54	89	128	21	52
28	45	80	137	30	43	90	127	20	53	88	129
135	82	47	26	133	84	49	24	131	86	51	22
46	27	134	83	48	25	132	85	50	23	130	87

En revanche un tel parcours existe pour n'importe quel échiquier carré dont la taille est un multiple de 4 autre que 4 ou 8^[18].

Il est à noter que quelques travaux sont menés sur le thème du parcours de cavalier au XXI^e siècle^[15].

Analyse mathématique[modifier | modifier le code]

Lien avec la théorie des graphes[modifier | modifier le code]

La recherche d'un tour du cavalier est un cas particulier des graphes hamiltoniens dans la théorie des graphes. De plus comme un cavalier passe toujours d'une case noire à une case blanche et vice-versa, il s'ensuit que le graphe des mouvements du cavalier est un graphe biparti.

Existence d'un parcours ouvert sur un échiquier rectangulaire[modifier | modifier le code]

Dans le cas d'une recherche d'un parcours ne bouclant pas nécessairement sur lui-même, il a été prouvé qu'il existe une solution pour tout échiquier rectangulaire dont la longueur et la largeur sont supérieures ou égales à 5^[20]^,^[21].

Existence d'un circuit fermé sur un échiquier rectangulaire[modifier | modifier le code]

Les tours de cavaliers peuvent se faire sur des damiers de différente taille et sur des formes différentes (rectangle, cube, pavé, spirale infinie, etc.), mais il est nécessaire que le nombre de cases soit pair. Dans le cas d'un échiquier rectangulaire on a le résultat d'existence suivant^[22]:

Théorème de Schwenk — Pour tout échiquier m × n tel que m soit inférieur ou égal à n, il existe un tour du cavalier, à moins qu'une des conditions suivantes (ou plus) ne soit vraie :

m et n sont impairs; n est différent de 1.
m = 1, 2, ou 4 ; n est différent de 1.
m = 3 et n = 4, 6 ou 8.

Condition 1[modifier | modifier le code]

La condition 1 empêche l'existence d'un tour fermé, pour de simples raisons de parité et de coloriage. Sur un échiquier noir et blanc standard, un cavalier se déplace du blanc vers le noir ou inversement. Donc un tour fermé doit visiter le même nombre de cases noires et blanches, et le nombre des cases visitées doit être pair. Or si m et n sont impairs, le nombre de cases est impair donc aucun tour fermé n'existe. Par contre il peut exister des tours ouverts.

Condition 2[modifier | modifier le code]

Selon cette condition, il n'existe pas de tour fermé si le plus petit côté est 1, 2, ou 4.

Si m = 1 ou 2, le cavalier ne peut pas atteindre toutes les cases (sauf dans le cas trivial 1 × 1). On peut aussi montrer l'absence de tour fermé dans le cas 4 × n par un argument de coloriage.

Le cavalier doit alterner vert et rouge.

Supposons qu'il existe un tour fermé sur un échiquier 4 × n. Appelons $A_{1}$ l'ensemble des cases noires et $A_{2}$ l'ensemble des cases blanches visitées par le tour, sur un échiquier noir et blanc standard. Regardons la figure de droite. Appelons $B_{1}$ l'ensemble des cases vertes et $B_{2}$ celui des cases rouges. Elles sont en nombre égal. Remarquons que le cavalier passe obligatoirement d'une case de $B_{1}$ à une case de $B_{2}$ . Comme il doit visiter chaque case, il doit aussi passer d'une case de $B_{2}$ à une case de $B_{1}$ (sinon il devrait parcourir deux cases consécutives ou plus de $B_{1}$ ensuite, ce qui est impossible).

L'examen de ce tour hypothétique donne une contradiction :

La première case du tour sera dans $A_{1}$ et $B_{1}$ . Sinon il suffit d'intervertir les définitions de $B_{1}$ et $B_{2}$ .
La seconde case doit être dans $A_{2}$ et $B_{2}$ .
La troisième case doit être dans $A_{1}$ et $B_{1}$ .
La quatrième case doit être dans $A_{2}$ et $B_{2}$ .
Et ainsi de suite.

Il en découle que les ensembles $A_{1}$ et $B_{1}$ sont confondus, tout comme les ensembles $A_{2}$ et $B_{2}$ . C'est absurde, donc aucun tour n'existe dans le cas 4 × n, et ce quel que soit n.

Condition 3[modifier | modifier le code]

On peut prouver la condition 3 au cas par cas. Rechercher un tour fermé dans les cas 3 × 4, 3 × 6, 3 × 8 échoue rapidement. Pour les cas 3 × n, avec n pair et plus grand que 8, on construit les tours fermés par récurrence, en répétant les mouvements.

Autres cas[modifier | modifier le code]

Nous avons prouvé l'inexistence d'un tour fermé dans les trois conditions mentionnées. Prouver l'existence d'un tel tour dans les autres cas est plus compliqué^[23].

Obtention effective d'un parcours du cavalier[modifier | modifier le code]

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Pour réussir un parcours, il suffit de choisir pour chaque nouveau saut une case libre parmi celle offrant le moins de sauts ultérieurs possibles, quitte à annuler les derniers coups en cas d'impasse : c'est un exercice classique de programmation.

Bien que le problème général de recherche d'un circuit hamiltonien dans un graphe soit NP-complet, le cas particulier du tour du cavalier peut être résolu en temps linéaire^[21].

Dénombrement des solutions[modifier | modifier le code]

Il y a 26 534 728 821 064 circuits fermés différents sur un échiquier carré de 64 cases^[24], et il y en a 9 862 sur un échiquier carré de 36 cases^[25].

Le nombre de parcours ouverts pour un échiquier carré est donné par suite A165134 de l'OEIS :

Dimension de l'échiquier :	1	2	3	4	5	6	7	8
Nombre de parcours ouverts :	1	0	0	0	1 728	6 637 920	165 575 218 320	19 591 828 170 979 904

Applications[modifier | modifier le code]

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Cryptographie[modifier | modifier le code]

Cette section est vide, insuffisamment détaillée ou incomplète. Votre aide est la bienvenue ! Comment faire ?

Le problème du cavalier a été proposé pour concevoir des schémas de chiffrement en cryptographie visuelle^[26];
Le problème a aussi été proposé pour la génération de nombres pseudo-aléatoires de qualité cryptographique^[27].

Littérature[modifier | modifier le code]

Rudrata, un poète du Cachemire de la fin du IX^e siècle (vers 825-850), propose un problème d'Euler rédigé en vers : « Les Ornements de la poésie », écrit en sanskrit, qui comporte un ensemble de versets basés sur des séries de syllabes en relation avec le parcours cavalier.
Mikhaïl W. Ramseier, dans son roman Nigrida, propose une intrigue qui tourne autour d'un cryptogramme basé sur un chiffre de Vigenère dissimulé au sein d'un problème du cavalier d'Euler.
Au XX^e siècle, le groupe d'écrivains Oulipo utilise ce problème. L'exemple le plus remarquable est le tour 10 × 10 qui détermine l'ordre des chapitres dans le livre de Georges Perec : La Vie mode d'emploi. Le même auteur a également utilisé un 9 × 9 dans Deux cent quarante-trois cartes postales en couleurs véritables.

Notes et références[modifier | modifier le code]

Notes[modifier | modifier le code]

↑ Le théorème de Schwenk (voir infra) permet en fait d'affirmer que les seuls échiquiers de largeur 3 pour lesquels il n'existe pas de circuit fermé ont pour longueur 2, 4, 6, 8 ou un nombre impair.
↑ La somme obtenue vaut alors un huitième de la somme totale des 64 numéros : ${\frac {64\times 65}{2}}\times {\frac {1}{8}}=260$ .
↑ D'autres sources mentionnent d'autres découvertes entre 1888 et 1970, il semble que ce soit Jeux et Stratégie qui a été mal informée
↑ Certains parcours peuvent être numérotés depuis plusieurs cases de départ, en prenant cela en compte il y a 140 parcours au total, aux symétries près.

Références[modifier | modifier le code]

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Knight's tour » (voir la liste des auteurs).

↑ La longueur maximale d'un parcours ouvert est donné par la suite A003192 de l'OEIS, et celle d'un parcours fermé par la suite A157416 de l'OEIS.
↑ C. Rajendran, "Caturanga movements described in Rudrata's Kavyalankara", dans Working-Papers "Indian Views", Förderkreis Scach-Geschichtsforschung e.V., novembre 2001.
↑ ^{a et b} Sesiano 2015, p. 163
↑ Sesiano 2015, p. 162
↑ ^{a et b} Sesiano 2015, p. 161
↑ ^{a et b} (en) « History of Magic Knight's Tour », sur mayhematics, 2004
↑ Sesiano 2015, p. 157
↑ Sesiano 2015, p. 159
↑ Sesiano 2015, p. 160
↑ Sesiano 2015, p. 165-167
↑ Sesiano 2015, p. 168
↑ Sesiano 2015, p. 169
↑ ^{a b c et d} Euler, Solution d'une question curieuse qui ne paraît soumise à aucune analyse, Mémoires de l'Académie Royale des Sciences et Belles Lettres, Année 1759, vol.15, pp.310-337, Berlin 1766
↑ Sesiano 2015
↑ ^{a b et c} Jean-Paul Delahaye, « Du flou et du faux en mathématiques », Pour la Science, n^o 516,‎ octobre 2020.
↑ ^{a et b} Pierre Berloquin, « Manœuvre de cavalerie », Jeux et Stratégie, n^o 18,‎ novembre-décembre 1982, p. 24-26.
↑ (en) Eric W. Weisstein, « There Are No Magic Knight's Tours on the Chessboard », sur MathWorld, 6 août 2003.
↑ ^{a et b} (en) [vidéo] Numberphile, Magic Chess Tours (with Knights and Kings) sur YouTube, 1^er avril 2024.
↑ (en) 12 by 12 Magic Knight's Tours.
↑ (en) P. Cull et J. De Curtins, « Knight's Tour Revisited », Fibonacci Quarterly, vol. 16,‎ 1978, p. 276–285 (lire en ligne)
↑ ^{a et b} (en) A. Conrad, T. Hindrichs, H. Morsy et I. Wegener, « Solution of the Knight's Hamiltonian Path Problem on Chessboards », Discrete Applied Mathematics, vol. 50, n^o 2,‎ 1994, p. 125–134 (DOI 10.1016/0166-218X(92)00170-Q)
↑ (en) Allen J. Schwenk, « Which Rectangular Chessboards Have a Knight’s Tour? », Mathematics Magazine,‎ 1991, p. 325–332
↑ (en) John J. Watkins, Across the Board : the Mathematics of Chessboard Problems, Princeton University Press, 2004, 257 p. (ISBN 978-0-691-11503-0, lire en ligne)
↑ (en) Brendan McKay, « Knight's Tours on an 8 × 8 Chessboard », Technical Report TR-CS-97-03, Department of Computer Science, Australian National University,‎ 1997 (lire en ligne)
↑ (en) Eric W. Weisstein, « Knight's Tour », sur MathWorld
↑ (en) Manpreet Singha, Ajay Kakkarb et Manjinder Singhc, « Image Encryption Scheme Based on Knight’s Tour Problem », Procedia Computer Science,‎ 2015 (lire en ligne).
↑ (en) Ali Shakir Mahmood et Mohd Shafry Mohd Rahim, « Generating and Expanding of an Encryption Key Based on the Knight's Tour Problem », Journal of Theoretical and Applied Information Technology, vol. 95, n^o 7,‎ 15 avril 2017 (lire en ligne).

Bibliographie[modifier | modifier le code]

[Sesiano15] Jacques Sesiano, Euler et le parcours du cavalier : Avec une annexe sur le théorème des polyèdres, Lausanne, Presses polytechniques et universitaires romandes, 2015, 272 p. (ISBN 978-2-88074-857-9, présentation en ligne, lire en ligne).

Articles connexes[modifier | modifier le code]

Twixt

Liens externes[modifier | modifier le code]

Sur les autres projets Wikimedia :

Problème du cavalier, sur Wikimedia Commons

(en) George Jelliss, « Knight's Tour Notes », sur mayhematics.com, 2000 - 2017 (consulté le 3 novembre 2017) : compilation de parcours de différentes époques, avec différentes règles et différentes formes de plateau.
La description du problème et quelques références par Georges Perec extrait de la revue l'Arc, n°78.
Une application en Flash pour jouer au problème du cavalier, sur procrastin.fr
(en) Programme pour résoudre le problème du cavalier, sur le blog de Dmitry Brant

[16] Le théorème de Schwenk (voir infra) permet en fait d'affirmer que les seuls échiquiers de largeur 3 pour lesquels il n'existe pas de circuit fermé ont pour longueur 2, 4, 6, 8 ou un nombre impair.

[17] La somme obtenue vaut alors un huitième de la somme totale des 64 numéros : ${\frac {64\times 65}{2}}\times {\frac {1}{8}}=260$ .

[19] D'autres sources mentionnent d'autres découvertes entre 1888 et 1970, il semble que ce soit Jeux et Stratégie qui a été mal informée

[21] Certains parcours peuvent être numérotés depuis plusieurs cases de départ, en prenant cela en compte il y a 140 parcours au total, aux symétries près.

[1] La longueur maximale d'un parcours ouvert est donné par la suite A003192 de l'OEIS, et celle d'un parcours fermé par la suite A157416 de l'OEIS.

[2] C. Rajendran, "Caturanga movements described in Rudrata's Kavyalankara", dans Working-Papers "Indian Views", Förderkreis Scach-Geschichtsforschung e.V., novembre 2001.

[Sesiano_p163-3] {a et b} Sesiano 2015, p. 163

[4] Sesiano 2015, p. 162

[Sesiano_p161-5] {a et b} Sesiano 2015, p. 161

[mayhematics-6] {a et b} (en) « History of Magic Knight's Tour », sur mayhematics, 2004

[7] Sesiano 2015, p. 157

[8] Sesiano 2015, p. 159

[9] Sesiano 2015, p. 160

[10] Sesiano 2015, p. 165-167

[11] Sesiano 2015, p. 168

[12] Sesiano 2015, p. 169

[Euler-13] {a b c et d} Euler, Solution d'une question curieuse qui ne paraît soumise à aucune analyse, Mémoires de l'Académie Royale des Sciences et Belles Lettres, Année 1759, vol.15, pp.310-337, Berlin 1766

[14] Sesiano 2015

[delahaye-15] {a b et c} Jean-Paul Delahaye, « Du flou et du faux en mathématiques », Pour la Science, n^o 516,‎ octobre 2020.

[jessie18-18] {a et b} Pierre Berloquin, « Manœuvre de cavalerie », Jeux et Stratégie, n^o 18,‎ novembre-décembre 1982, p. 24-26.

[20] (en) Eric W. Weisstein, « There Are No Magic Knight's Tours on the Chessboard », sur MathWorld, 6 août 2003.

[numberphile-22] {a et b} (en) [vidéo] Numberphile, Magic Chess Tours (with Knights and Kings) sur YouTube, 1^er avril 2024.

[23] (en) 12 by 12 Magic Knight's Tours.

[Cull1978-24] (en) P. Cull et J. De Curtins, « Knight's Tour Revisited », Fibonacci Quarterly, vol. 16,‎ 1978, p. 276–285 (lire en ligne)

[Conrad1994-25] {a et b} (en) A. Conrad, T. Hindrichs, H. Morsy et I. Wegener, « Solution of the Knight's Hamiltonian Path Problem on Chessboards », Discrete Applied Mathematics, vol. 50, n^o 2,‎ 1994, p. 125–134 (DOI 10.1016/0166-218X(92)00170-Q)

[26] (en) Allen J. Schwenk, « Which Rectangular Chessboards Have a Knight’s Tour? », Mathematics Magazine,‎ 1991, p. 325–332

[27] (en) John J. Watkins, Across the Board : the Mathematics of Chessboard Problems, Princeton University Press, 2004, 257 p. (ISBN 978-0-691-11503-0, lire en ligne)

[28] (en) Brendan McKay, « Knight's Tours on an 8 × 8 Chessboard », Technical Report TR-CS-97-03, Department of Computer Science, Australian National University,‎ 1997 (lire en ligne)

[29] (en) Eric W. Weisstein, « Knight's Tour », sur MathWorld

[30] (en) Manpreet Singha, Ajay Kakkarb et Manjinder Singhc, « Image Encryption Scheme Based on Knight’s Tour Problem », Procedia Computer Science,‎ 2015 (lire en ligne).

[31] (en) Ali Shakir Mahmood et Mohd Shafry Mohd Rahim, « Generating and Expanding of an Encryption Key Based on the Knight's Tour Problem », Journal of Theoretical and Applied Information Technology, vol. 95, n^o 7,‎ 15 avril 2017 (lire en ligne).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[N 1]

[N 2]

[16]

[N 3]

[17]

[N 4]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

Variantes[modifier | modifier le code]

Selon les pièces[modifier | modifier le code]

Selon les formes de plateau[modifier | modifier le code]

Selon les parcours[modifier | modifier le code]

Histoire[modifier | modifier le code]

Inde[modifier | modifier le code]

Monde arabe[modifier | modifier le code]

Circuit fermé[modifier | modifier le code]

Autres règles de parcours[modifier | modifier le code]

Occident[modifier | modifier le code]

Pendant le Moyen Âge et la Renaissance[modifier | modifier le code]

Au début du XVIIIe siècle[modifier | modifier le code]

Les travaux d'Euler[modifier | modifier le code]

Études ultérieures[modifier | modifier le code]

Analyse mathématique[modifier | modifier le code]

Lien avec la théorie des graphes[modifier | modifier le code]

Existence d'un parcours ouvert sur un échiquier rectangulaire[modifier | modifier le code]

Existence d'un circuit fermé sur un échiquier rectangulaire[modifier | modifier le code]

Condition 1[modifier | modifier le code]

Condition 2[modifier | modifier le code]

Condition 3[modifier | modifier le code]

Autres cas[modifier | modifier le code]

Obtention effective d'un parcours du cavalier[modifier | modifier le code]

Dénombrement des solutions[modifier | modifier le code]

Applications[modifier | modifier le code]

Cryptographie[modifier | modifier le code]

Littérature[modifier | modifier le code]

Notes et références[modifier | modifier le code]

Notes[modifier | modifier le code]

Références[modifier | modifier le code]

Bibliographie[modifier | modifier le code]

Articles connexes[modifier | modifier le code]

Liens externes[modifier | modifier le code]

Au début du XVIII^e siècle[modifier | modifier le code]