Nombre constructible

Si ce bandeau n'est plus pertinent, retirez-le. Cliquez ici pour en savoir plus.

Certaines informations figurant dans cet article ou cette section devraient être mieux reliées aux sources mentionnées dans les sections « Bibliographie », « Sources » ou « Liens externes » (avril 2017).

Vous pouvez améliorer la vérifiabilité en associant ces informations à des références à l'aide d'appels de notes.

Représentation des nombres irrationnels selon la répartition des réels en nombres rationnels, constructibles, algébriques et transcendants. Cliquez sur un des nombres du schéma pour plus d'informations concernant l'élément choisi. (Image source) v · d · m

Un nombre constructible (sous-entendu à la règle et au compas) est la mesure d'une longueur associée à deux points constructibles à la règle (non graduée) et au compas. Ainsi, √2 est un nombre constructible, mais ni ³√2 ni $π$ ne le sont.

C'est effectivement en termes de longueurs que pensaient les mathématiciens grecs et ceux qui, à leur suite, ont cherché à déterminer quels étaient les points et les nombres constructibles de cette façon.

Du temps de la mathématique grecque, on distinguait les problèmes dont les solutions ne faisaient intervenir que des droites et des cercles dans le plan, de ceux faisant intervenir d'autres procédés (utilisation de courbes dites « mécaniques » telles la spirale d'Archimède ou les conchoïdes, utilisation de coniques pour les problèmes dits solides…). Cette distinction est à la source de problèmes célèbres comme la quadrature du cercle, la trisection de l'angle et la duplication du cube.

Les mathématiciens, jusqu'au XVII^e siècle, n'accordaient aucune réalité concrète aux nombres négatifs. Il est cependant commode d'appliquer la définition, non seulement à des longueurs, mais également à des coordonnées de points constructibles.

Définition d'un nombre constructible[modifier | modifier le code]

On donne ici une définition mathématique précise de la notion de point constructible (sous-entendu, à la règle et au compas).

Points constructibles[modifier | modifier le code]

Points constructibles en une étape[modifier | modifier le code]

Soit E un sous-ensemble du plan euclidien, qu'on assimile ici à ℝ ². On dit qu'un point P = (x, y) est constructible en une étape à partir de E si P est un point de E ou si P est dans l'intersection de deux objets distincts parmi :

l'ensemble des droites qui passent par deux éléments distincts de E ;
l'ensemble des cercles centrés en un point de E et dont le rayon est la distance de deux quelconques points de E.

On note C₁(E) l'ensemble des points constructibles en une étape à partir de E.

On peut remarquer que si E est fini, alors, C₁(E) l'est aussi.

Points constructibles en n étapes[modifier | modifier le code]

Partant des mêmes données, on définit, naturellement et par récurrence, l'ensemble C_n(E) des points constructibles en $n$ étapes à partir de E. Pour $n$ = 1, c'est la construction précédente. Sinon, on pose :

C_{n+1}(E)=C_{1}\left(C_{n}(E)\right).

Points constructibles[modifier | modifier le code]

Enfin, l'ensemble des points constructibles à partir de E, qu'on note C(E), est la réunion (croissante) des C_n(E), c'est-à-dire : un point P est dit constructible à partir de E s'il existe $n$ tel que P soit constructible en $n$ étapes.

C(E)=\bigcup _{n=1}^{\infty }C_{n}(E).

Nombres constructibles[modifier | modifier le code]

On se place dans le même cadre, c'est-à-dire le plan euclidien assimilé à ℝ² ; on se donne E un sous-ensemble de ℝ².

Un nombre réel est dit constructible à partir de E s'il est l'abscisse d'un point constructible à partir de E.

Un nombre constructible est un nombre qui est constructible à partir de l'ensemble { (0,0), (0,1) }^[1].

Rappel sur quelques constructions possibles[modifier | modifier le code]

Article détaillé : Construction à la règle et au compas.

À l'aide d'une règle et d'un compas, on peut construire des cercles et des droites, bien sûr, mais aussi des parallèles et des perpendiculaires :

Parallèle à une droite (AB) passant par un point C.

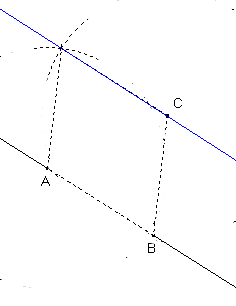
On construit le quatrième point X du parallélogramme ABCX en :

traçant un arc de cercle de centre C et de rayon BA ;
et un arc de cercle de centre A et de rayon BC ;

Perpendiculaire à une droite (AB) passant par un point C extérieur à cette droite ; symétrique d'un point C par rapport à une droite (AB).

On utilise les propriétés des symétries axiales en traçant :

le cercle de centre A passant par C ;
le cercle de centre B passant par C.

Ces cercles (si C n'appartient pas à la droite (AB)), ont deux points d'intersection : C et un autre point C' tel que la droite (CC') est perpendiculaire à (AB). On peut remarquer que C' est le symétrique du point C par rapport à la droite (AB).

Symétrique d'un point C par rapport à un point A.

Le cercle de centre A passant par C et la droite (AC) ont deux points d'intersection : C et C', tel que C' est le symétrique de C par rapport à A.

Construction d'une parallèle
Construction d'une perpendiculaire

Opération sur les nombres constructibles[modifier | modifier le code]

Addition et soustraction[modifier | modifier le code]

L'addition et la soustraction ne nécessitent que deux opérations : tracer un segment de droite de longueur x puis un segment de longueur y, aligné au premier ; en le traçant dans le même sens, on obtient un segment de longueur x + y, et dans le sens opposé, à condition que x > y, cela donne un segment de longueur x – y.

Somme
Différence

Multiplication[modifier | modifier le code]

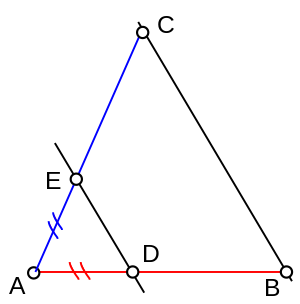
À partir d'un point A, on trace une droite passant par A et on y place E tel que AE = 1, et B tel que AB = b. Sur une droite passant par E non confondue avec la première, on place C tel que CE = a et on trace la droite AC. On trace enfin la parallèle à EC passant par B, qui croise AC en D. Alors BD = a×b.

En effet, une simple utilisation du théorème de Thalès permet de montrer que BD est égal au produit des distances AB et CE.

Division[modifier | modifier le code]

C'est l'opération réciproque de la précédente, s'appuyant également sur le théorème de Thalès.

Ces observations permettent de dire que l'ensemble des nombres constructibles (si on accepte les distances négatives) est un corps commutatif. Les Grecs ont ainsi pu établir que tous les nombres rationnels positifs étaient constructibles. Mais leur première surprise est venue de la dernière opération.

Extraction de racine carrée[modifier | modifier le code]

On peut utiliser le théorème de la moyenne géométrique qui établit que, dans un triangle AFD rectangle en F, si B est le pied de la hauteur issue de F, on a

BD×BA = FB²

C'est une conséquence immédiate du fait que les triangles ABF et FBD sont semblables.

Pour construire la racine carrée d'un nombre $p$ , on trace donc un segment [AD] dont la longueur est égale à $p + 1$ , puis un demi-cercle de diamètre AD, ensuite le point B sur [AD] tel que DB soit égal à 1, enfin la perpendiculaire à (AD) menée par B, qui rencontre le demi-cercle en un point F. D'après le théorème de Thalès sur le cercle, le triangle AFD est rectangle en F. On en déduit l'égalité $FB 2 = 1\times p$ , qui assure que BF= $\sqrt p$ .

Les racines carrées sont donc constructibles.

Exemples vidéos[modifier | modifier le code]

Addition de a et b
Différence de a et b
Produit de a et b
Division de a par b
Racine carrée de p

Ensemble des nombres constructibles[modifier | modifier le code]

Les opérations précédentes permettent donc de dire que tout rationnel est constructible, mais aussi que la racine carrée d'un rationnel positif est constructible et même que l'on peut construire un nombre comme

5+{\sqrt {23-{\frac {3/2+{\sqrt {17}}}{{\sqrt {3}}-{\sqrt {\sqrt {2}}}}}}}.

L'intuition semble dire que les seuls nombres constructibles sont ceux pouvant s'écrire uniquement à l'aide des 5 opérations précédentes. Il faut attendre les travaux de Pierre-Laurent Wantzel qui, grâce à ceux de Gauss sur les polygones constructibles, peut énoncer son théorème et affirmer que les seuls nombres constructibles sont ceux de cette forme (plus exactement sont dans une extension quadratique d'une extension quadratique… d'une extension quadratique de ℚ). Une telle construction s'appelle une tour d'extensions quadratiques.

On peut exprimer ce résultat différemment : l'ensemble des nombres constructibles (à la règle et au compas) est le plus petit sous-corps de ℝ stable par racine carrée, ou encore le plus petit corps euclidien.

Grâce à ce théorème, tombent deux des problèmes de l'Antiquité : la trisection de l'angle et la duplication du cube, qui reviennent à résoudre une équation de degré 3 (donc extension impaire). L'ensemble des nombres constructibles ne regroupe donc qu'une petite partie de l'ensemble des nombres algébriques. L'article « Tour d'extensions quadratiques » propose une démonstration rigoureuse de ces résultats.

Le problème de la quadrature du cercle tombera un peu plus tard, quand Ferdinand von Lindemann aura prouvé en 1882 que $π$ n'est pas algébrique, c’est-à-dire n'est solution d'aucune équation de degré n à coefficients dans ℚ. le nombre $π$ ne peut donc pas se trouver dans une extension quadratique d'une extension quadratique… d'une extension quadratique de ℚ.

Exemples de nombres non constructibles[modifier | modifier le code]

Tous les nombres transcendants.
Pour tout entier d > 0 qui n'est pas une puissance de 2, tous les nombres algébriques de degré d. On en construit facilement à l'aide :
- du critère d'Eisenstein : par exemple ${\sqrt[{d}]{4n+2}}$ ;
- du théorème de Gauss-Wantzel : par exemple cos(2π/n) si 2d est de plus l'indicatrice d'Euler d'un entier n, comme cos(2π/7), cos(2π/9), cos(π/7) et cos(π/9) pour d = 3, ou cos(2π/11) et cos(π/11) pour d = 5, etc. ;
Pour d égal à une puissance de 2, certains nombres^[2] algébriques de degré d, comme les racines du polynôme X^d – X – 1^[3].

Variantes de constructibilités et liens avec la constructibilité à la règle et au compas[modifier | modifier le code]

On obtient des variantes de nombres constructibles :

soit en affaiblissant les outils utilisés (utilisation de la règle seule, utilisation du compas seul, utilisation de la règle et du compas dont l'ouverture est bloquée, utilisation de la règle et du compas à pointes sèches permettant seulement de reporter des longueurs, utilisation de la règle et de l'empan permettant seulement de reporter des segments de longueur unité). On obtient des sous-ensembles des nombres constructibles, qui peuvent parfois être égaux à l'ensemble des nombres constructibles.
soit en renforçant les outils utilisés (utilisation du compas et de la règle graduée, utilisation de coniques ou d'autres courbes auxiliaires). On obtient une extension des nombres constructibles.
soit en utilisant d'autres procédés de construction (origami par exemple, ou miroir semi-réfléchissant^[4]). L'ensemble de nombres constructibles par origami dépend des règles que l'on s'autorise à employer.

Constructibilité uniquement à la règle[modifier | modifier le code]

Article détaillé : Construction à la règle seule.

Des points de bases étant donnés, un point est constructible à la règle s'il est point d'intersection de deux droites, chacune de ces deux droites passant par deux points qui sont des points de base ou des points déjà construits.

Les propriétés d'une figure constructible sont conservées par projection centrale. Ce n'est pas le cas pour les milieux, les parallèles ou les symétries.

Il est démontré qu'il est impossible avec uniquement une règle de construire le milieu d'un segment, ou de mener par un point une parallèle à une droite.

Cependant, le théorème de Poncelet-Steiner énonce que, si on se donne un cercle et son centre, alors il est possible avec la règle seule de construire tout point constructible à la règle et au compas. Il en est de même si on se donne deux cercles sécants sans leur centre, ou bien trois cercles non sécants. Ainsi, les centres de deux cercles sécants peuvent être déterminés avec la règle seule.

Constructibilité à la règle et à l'empan[modifier | modifier le code]

L'empan permet uniquement de reporter des segments de longueur unité sur une droite. Au moyen de la règle et de l'empan, on est capable de mener une parallèle à une droite donnée, passant par un point P donné, ce qu'on ne peut faire avec la règle seule^[5].

Soit A un point quelconque de la droite, [AB] et [BC] égaux à l'empan sur cette droite. Soit D un point de (AP). On trace (DB) et (PC) qui se coupent en E. On trace (AE) et (DC) qui se coupent en F. (PF) est la parallèle cherchée.

Sachant tracer des parallèles, on sait également compléter un parallèlogramme à partir de trois de ces points et donc reporter un segment de longueur quelconque sur une droite parallèle. Plus généralement, on sait reporter un segment de longueur donnée sur une droite quelconque donnée.

Soit le segment [AB] à reporter sur la droite (AC). On trace D et E tels que AD et AE soient égaux à l'empan. On trace la droite (DE) puis la parallèle (BC) à (DE) passant par B. Le segment [AC] est le report cherché.

Il en résulte que les constructions à la règle et à l'empan sont équivalentes aux constructions à la règle et au compas à pointes sèches, traitées dans le paragraphe suivant.

Constructibilité à la règle et au compas à pointes sèches[modifier | modifier le code]

Le compas à pointes sèches est un instrument permettant de reporter des longueurs sur des droites, mais non de tracer des cercles. L'ensemble des nombres constructibles à la règle et au compas à pointes sèches est strictement inclus dans l'ensemble des nombres constructibles à la règle et au compas^[6]. Il s'agit du plus petit corps contenant les rationnels et stable par la fonction $\scriptstyle x\to {\sqrt {1+x^{2}}}$ . Ses éléments sont les nombres constructibles à la règle et au compas qui sont totalement réels^[7]. Les nombres √2 et $\scriptstyle {\sqrt {2+{\sqrt {2}}}}$ sont constructibles à la règle et au compas à pointes sèches, mais $\scriptstyle {\sqrt {1+{\sqrt {2}}}}$ ne l'est pas, alors qu'il est constructible à la règle et au compas. Il en résulte que, si on peut construire avec la règle et le compas à pointes sèches un triangle rectangle dont on donne les longueurs des deux côtés de l'angle droit, on ne sait pas nécessairement construire un triangle rectangle dont on connaît la longueur d'un côté et de l'hypoténuse. Autrement dit, la règle et le compas à pointes sèches permettent de construire la racine carrée de la somme de deux carrés, mais pas la racine carrée de la différence de deux carrés.

Les polygones réguliers constructibles à la règle et au compas le sont également à la règle et au compas à pointes sèches.

Les nombres constructibles à la règle et au compas à pointes sèches sont également ceux que l'on peut construire avec une règle et un bissecteur d'angle (y compris de l'angle plat), ou encore en utilisant les axiomes 1), 2), 3) et 4) des origamis.

Voici quelques exemples de constructions.

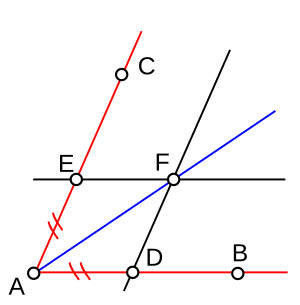
Construction d'une bissectrice avec la règle et l'empan

Soit à tracer une bissectrice de (AB) et (AC). On porte les points D et E tels que AD = AE. On trace les parallèles à (AB) et (AC) passant par D et E (ce qu'on sait faire). L'intersection de ces deux parallèles donne un point F tel que (AF) est bissectrice.

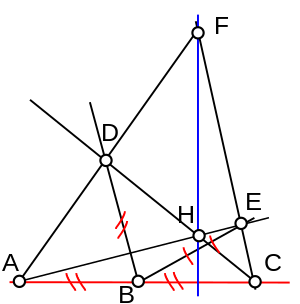
Construction d'une perpendiculaire avec la règle et l'empan

Soit à construire une perpendiculaire à une droite donnée. On prend A, B et C sur cette droite de façon que AB = BC. On trace également deux segments [BD] et [BE] de longueur égale à AB. Soit F l'intersection de (AD) et (CE). ADC est rectangle en D, et AEC en E, de sorte que (AE) et (CD) sont deux hauteurs du triangle ACF. Si H est l'intersection de (AE) et (CD), il suffit de tracer (FH) pour avoir la troisième hauteur. On peut alors, quitte à tracer une parallèle à la perpendiculaire précédemment construite, tracer la perpendiculaire à la droite passant par un point donné.

Constructibilité uniquement au compas[modifier | modifier le code]

Le théorème de Mohr-Mascheroni, montré par Georg Mohr, puis par Lorenzo Mascheroni en 1797, affirme que si une construction géométrique est possible à la règle et au compas, alors elle est possible au compas seul.

Voir aussi le problème de Napoléon qui consiste à construire au compas seul le centre d'un cercle donné, ainsi que la construction du carré au compas seul.

Constructibilité par origami[modifier | modifier le code]

Article détaillé : Mathématiques des origamis.

Les constructions par origami sont les constructions géométriques par pliages de papier. Dans leur développement le plus complet, ces constructions permettent de construire tous les nombres constructibles à la règle et au compas, mais également de trisecter un angle ou de dupliquer un cube. Les constructions par origami sont équivalentes aux constructions utilisant la règle et les coniques de foyer, de directrice et d'excentricité constructibles.^{[réf. nécessaire]}

Constructibilité à la règle graduée et au compas[modifier | modifier le code]

Article détaillé : Neusis.

La règle graduée est une règle munie de deux graduations dont l'écart figure l'unité de longueur. Jointe au compas, la règle graduée est plus puissante que les méthodes utilisant les intersections de coniques utilisées par les Grecs anciens pour résoudre les problèmes dits solides. Les deux instruments permettent de construire tous les points du plan complexe obtenus à partir des rationnels en itérant résolution d'équation du deuxième ou du troisième degré, et de résoudre certains problèmes faisant intervenir des équations du cinquième ou du sixième degré. Ils résolvent en particulier les problèmes de la trisection de l'angle et de la duplication du cube et permettent par exemple la construction de l'heptagone régulier, de l'ennéagone régulier et des polygones réguliers de 11^[8], 13, 19 ou 27 côtés. Ils ne permettent pas de construire les polygones réguliers de 23, 29, 43 ou 47 côtés. La question reste ouverte pour les polygones réguliers de 25, 31, 41 ou 61 côtés^[9].

Voici par exemple comment on construit la racine cubique d'un nombre d inférieur à 1.

Soit OA = d, OF = 3d. On construit le triangle rectangle OAG de façon que AG soit égale à l'unité, longueur séparant les deux graduations de la règle. On trace la parallèle (AH) à (FG) passant par A. Toutes ces constructions se font à la règle et au compas. On utilise alors la règle graduée en la faisant passer par G, l'une des graduations devant être sur (AH), l'autre graduation sur (OA). Une fois cette disposition atteinte, AB est égal à 2d^1/3.

La règle graduée permet des constructions par ajustement (ou neusis). On peut la faire passer par un point pendant qu'une des graduations parcourt une courbe (droite ou cercle) donnée, jusqu'à ce que l'autre graduation atteigne une autre courbe donnée. Cette deuxième graduation parcourt alors une conchoide de la première courbe, et l'utilisation de la règle graduée revient à accepter comme constructibles les intersections de conchoïde et de cercle, ou de conchoïde et de droite. Cependant, il n'y a pas de possibilité de tracer la conchoïde et la règle graduée ne permet pas de construire l'intersection de deux conchoïdes.

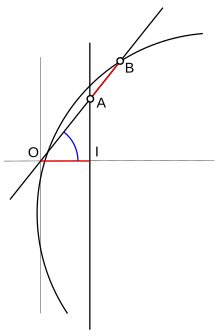
Voici par exemple comment on peut construire un angle de 2 $π$ /7. On construit à la règle et au compas le cercle de centre (18/5, –2√7/5) et de rayon √337/5. On dispose la règle de façon qu'elle passe par l'origine O, que la première graduation A soit sur la droite x = 1 et la seconde B sur le cercle. La règle forme alors un angle de 2 $π$ /7 avec (OI)^[10].

Rajouter de nouvelles graduations à la règle par rapport aux deux existantes n'apporte aucun bénéfice.

Constructibilité avec des allumettes[modifier | modifier le code]

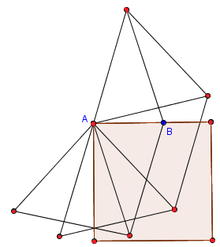
Construction d'un carré donné par un sommet A et un point B d'un côté adjacent à A à l'aide d'allumettes de même longueur^[11].

Les nombres constructibles avec des allumettes, c'est-à-dire des segments ayant tous la même longueur $l$ ^[a], sont exactement ceux qui sont constructibles à la règle et au compas^[12].

Notes et références[modifier | modifier le code]

Notes[modifier | modifier le code]

↑
Les opérations élémentaires sont au nombre de trois :
- Poser une allumette passant par deux points A et B séparés par une distance inférieure à $l$ ;
- Poser une allumette dont les extrémités sont un point A donné et un point sur une droite dont la distance à A est inférieur à $l$ ;
- Construire un triangle isocèle donné par sa base de longueur inférieure à $c=2l$ dont la longueur des côtés égaux vaut $l$ .

Références[modifier | modifier le code]

↑ A. Bouvier, M. Georges et F. Le Lyonnais, Dictionnaire des mathématiques, PUF, 4^e éd., 1993, p. 190.
↑ Voir Théorème d'Abel (algèbre)#Contre-exemples en tout degré supérieur ou égal à 5.
↑ Voir Théorie de Galois inverse#Quelques résultats.
↑ (en) John W. Emert, Kay I. Meeks et Roger B. Nelson, « Reflections on a mira », Amer. Math. Monthly, vol. 101, n^o 6,‎ juin-juillet 1994, p. 544-549 (DOI 10.2307/2975320).
↑ David Hilbert, Les fondements de la géométrie, rééd. Gabay (1995), p. 159-167.
↑ (en) Roger C. Alperin (de), « Trisections and totally real origamis », Amer. Math. Monthly,, vol. 112, n^o 3,‎ mars 2005, p. 200-211 (arXiv math/0408159).
↑ (en) David Auckly et John Cleveland, « Totally real origami and impossible paper folding », Amer. Math. Monthly, vol. 102, n^o 3,‎ mars 1995, p. 215-226 (arXiv math/0407174).
↑ (en) B. Elliot et C. Snyder, Mathematical Proceedings of the Cambridge Philosophical Society, 156.3 (mai 2014): 409-424. (exposé en ligne).
↑ (en) Arthur Baragar, « Constructions using a compass and twice-notched straightedge », Amer. Math. Monthly, vol. 109, n^o 2,‎ février 2002, p. 151-164 (lire en ligne).
↑ Gérard Lavau, « L'heptagone régulier », Feuille de Vigne, IREM de Dijon, vol. 86,‎ octobre 2002, p. 19-25.
↑ [vidéo] Deux (deux ?) minutes pour la quadrature du cercle. sur YouTube : construction animée d'un carré en allumettes à partir de 17'51.
↑ (en) T. R. Dawson, « 'Match-Stick' Geometry », The Mathematical Gazette, vol. 23, n^o 254,‎ mai 1939 (lire en ligne).

Ouvrages[modifier | modifier le code]

Jean-Claude Carrega, Théorie des corps - La règle et le compas [détail de l’édition]
David Hilbert, Les fondements de la géométrie, rééd. Dunod (1971) ou Gabay (1997)

[12] Les opérations élémentaires sont au nombre de trois :
Poser une allumette passant par deux points A et B séparés par une distance inférieure à $l$ ;

Poser une allumette dont les extrémités sont un point A donné et un point sur une droite dont la distance à A est inférieur à $l$ ;

Construire un triangle isocèle donné par sa base de longueur inférieure à $c=2l$ dont la longueur des côtés égaux vaut $l$ .

[2] Poser une allumette passant par deux points A et B séparés par une distance inférieure à $l$ ;

[3] Poser une allumette dont les extrémités sont un point A donné et un point sur une droite dont la distance à A est inférieur à $l$ ;

[4] Construire un triangle isocèle donné par sa base de longueur inférieure à $c=2l$ dont la longueur des côtés égaux vaut $l$ .

[1] A. Bouvier, M. Georges et F. Le Lyonnais, Dictionnaire des mathématiques, PUF, 4^e éd., 1993, p. 190.

[2] Voir Théorème d'Abel (algèbre)#Contre-exemples en tout degré supérieur ou égal à 5.

[3] Voir Théorie de Galois inverse#Quelques résultats.

[4] (en) John W. Emert, Kay I. Meeks et Roger B. Nelson, « Reflections on a mira », Amer. Math. Monthly, vol. 101, n^o 6,‎ juin-juillet 1994, p. 544-549 (DOI 10.2307/2975320).

[5] David Hilbert, Les fondements de la géométrie, rééd. Gabay (1995), p. 159-167.

[6] (en) Roger C. Alperin (de), « Trisections and totally real origamis », Amer. Math. Monthly,, vol. 112, n^o 3,‎ mars 2005, p. 200-211 (arXiv math/0408159).

[7] (en) David Auckly et John Cleveland, « Totally real origami and impossible paper folding », Amer. Math. Monthly, vol. 102, n^o 3,‎ mars 1995, p. 215-226 (arXiv math/0407174).

[8] (en) B. Elliot et C. Snyder, Mathematical Proceedings of the Cambridge Philosophical Society, 156.3 (mai 2014): 409-424. (exposé en ligne).

[9] (en) Arthur Baragar, « Constructions using a compass and twice-notched straightedge », Amer. Math. Monthly, vol. 109, n^o 2,‎ février 2002, p. 151-164 (lire en ligne).

[10] Gérard Lavau, « L'heptagone régulier », Feuille de Vigne, IREM de Dijon, vol. 86,‎ octobre 2002, p. 19-25.

[11] [vidéo] Deux (deux ?) minutes pour la quadrature du cercle. sur YouTube : construction animée d'un carré en allumettes à partir de 17'51.

[13] (en) T. R. Dawson, « 'Match-Stick' Geometry », The Mathematical Gazette, vol. 23, n^o 254,‎ mai 1939 (lire en ligne).

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[a]

[12]

v · m Notion de nombre
Ensembles usuels	Entier naturel ( $\scriptstyle \mathbb {N}$ ) Entier relatif ( $\scriptstyle \mathbb {Z}$ ) Nombre décimal ( $\scriptstyle \mathbb {D}$ ) Nombre rationnel ( $\scriptstyle \mathbb {Q}$ ) Nombre réel ( $\scriptstyle \mathbb {R}$ ) Nombre complexe ( $\scriptstyle \mathbb {C}$ )
Extensions	Quaternion ( $\scriptstyle \mathbb {H}$ ) Octonion ( $\scriptstyle \mathbb {O}$ ) Sédénion ( $\scriptstyle \mathbb {S}$ ) Nombre complexe déployé Tessarine Nombre bicomplexe ( $\scriptstyle \mathbb {C} _{2}$ ) Nombre multicomplexe ( $\scriptstyle \mathbb {C} _{n}$ $\scriptstyle {\mathcal {M}}\mathbb {C} _{n}$ ) Biquaternion Coquaternion Quaternion hyperbolique Octonion déployé Nombre hypercomplexe Nombre p-adique ( $\scriptstyle \mathbb {Q} _{p}$ ) Nombre hyperréel Nombre superréel Nombre dual Droite réelle achevée Nombre cardinal Nombre ordinal Nombre surréel Nombre pseudo-réel
Propriétés particulières	Parité Nombre premier Nombre composé Nombre figuré Nombre parfait Nombre positif Nombre négatif Fraction dyadique Nombre irrationnel Nombre algébrique Nombre transcendant Nombre imaginaire pur Nombre de Liouville Période Nombre normal Nombre univers Nombre constructible Nombre réel calculable Nombre transfini Infiniment petit
Exemples	Pi ( $π$ ) Racine carrée de deux ( $\scriptstyle {\sqrt {2}}$ ) Nombre d’or (φ) Zéro (0) Unité imaginaire ( $i$ ) Constante de Neper ( $e$ ) Aleph-zéro (ℵ₀) Table de constantes mathématiques
Articles liés	Chiffre Numération Fraction Opération Calcul Algèbre Arithmétique Suite d'entiers Infini ( $\infty$ ) Chiffre significatif