Effet dynamo
En astrophysique, la théorie de l'effet dynamo traite des cas dans lesquels un objet conducteur, un corps céleste ou une planète, engendre un champ magnétique lorsqu'il est parcouru par un courant électrique. La théorie physique sous-jacente est analogue à celle qui décrit l'effet dynamo en électrotechnique.
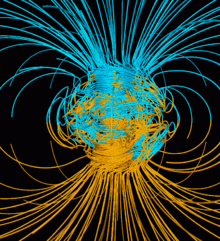
Ces phénomènes inductifs permettent d'expliquer la formation d'un champ magnétique autour d'un astre, tels que celui de la Terre, par effet dynamo terrestre, celui du Soleil, par dynamo solaire, ou ceux autour d'autres planètes ou étoiles.
Des progrès dans ce domaine pourraient permettre de mieux comprendre certains problèmes de magnétohydrodynamique et expliquer certaines propriétés du Soleil et des magnétars (un certain type d'étoiles à neutrons).
Historique[modifier | modifier le code]
Dans de Magnete (en) publié en 1600, William Gilbert conclut que la Terre possède un magnétisme permanent, comme celui de la magnétite. L'observation du dipôle magnétique terrestre, qui comprend une grande partie du champ magnétique de la Terre et qui, selon les observations de l'époque, semblait fixe avec une déviation d'environ 11 degrés par rapport à l'axe de rotation terrestre, entretenait cette idée.
En 1919, Joseph Larmor suggère qu'une dynamo puisse engendrer le champ[1],[2]. Cependant, il tente d'expliquer ce dernier en relation avec le champ magnétique du Soleil. Larmor ne convainc pas ses pairs. L'application des théories de Carl Friedrich Gauss aux observations magnétiques montre que le champ magnétique de la Terre est interne plutôt qu'externe.
D'autres scientifiques proposent des explications alternatives. Einstein suppose qu'il pourrait y avoir une asymétrie entre les charges de l'électron et du proton qui, à l'échelle de la Terre entière, produirait son champ magnétique. Patrick Blackett, quant à lui, tente une série d'expérimentations pour trouver une relation fondamentale entre le moment angulaire et le moment magnétique, mais n'aboutit à rien[3],[4].
Walter M. Elsasser, considéré comme le « père » de la présente théorie sur l'effet dynamo terrestre, soutient que le magnétisme est engendré par les courants électriques induits dans le noyau liquide externe de la Terre. Il est l'un des premiers à effectuer l'étude de l'orientation magnétique des minéraux dans les roches, quantifiant ainsi la variation du champ magnétique terrestre en fonction du temps.
Afin d'entretenir le champ magnétique contre la dissipation ohmique (qui se produirait pour le champ dipolaire dans 20 000 ans), le noyau externe doit subir des mouvements de convection.
Jusqu'ici, la modélisation numérique du champ magnétique terrestre n'a pas encore été démontrée avec succès, mais elle semble réalisable. Les premiers modèles sont axés sur la génération du champ dû aux mouvements de convection dans le noyau liquide de la planète. Il a été possible de démontrer la génération d'un champ aussi puissant que celui de la Terre lorsque le modèle a présumé une température uniforme à la surface du noyau et une viscosité exceptionnellement élevée du magma fluide. Les calculs qui incluent des paramètres plus réalistes donnent des valeurs du champ magnétique qui sont inférieures à celui mesuré, mais ouvrent aussi la voie au raffinement des modèles actuels qui pourraient finalement conduire à un seul modèle analytique précis. Ainsi, de très petites variations dans la température de la surface du noyau terrestre, d'ordre de quelques millikelvins, provoquent d'importantes augmentation du flux de convection et produit un champ magnétique plus réaliste[5],[6].
Définition formelle[modifier | modifier le code]
La théorie de l'effet dynamo décrit le processus par lequel une rotation avec un mouvement de convection dans un fluide conductible agit pour maintenir un champ magnétique. Cette théorie est utilisée pour expliquer la présence de champs magnétiques à long terme dans les corps astronomiques. Dans le cas terrestre, le fluide conducteur est le fer liquide situé dans le noyau externe. Dans le cas de la dynamo solaire, il s'agit d'un gaz ionisé à la tachocline. La théorie de la dynamo de corps astrophysiques utilise des équations de magnétohydrodynamique pour étudier comment le fluide peut régénérer en permanence le champ magnétique.
Il y a trois conditions requises à une dynamo pour fonctionner:
- Un milieu composé d'un fluide conducteur électrique,
- De l'énergie cinétique fournie par la rotation,
- Une source d'énergie interne pour conduire les mouvements convectifs au sein du fluide[7].
Dans le cas de la Terre, le champ magnétique est induit et constamment mis à jour par la convection du fer liquide dans le noyau externe. La rotation différentielle dans le noyau externe est fournie par la force de Coriolis due à la rotation de la Terre. La force de Coriolis tend ainsi à entraîner le mouvement des fluides et des courants électriques dans des colonnes (en) alignés avec l'axe de rotation.
Le champ magnétique (B) dépend de la vitesse (u), du temps (t), de la perméabilité magnétique () et de la diffusivité magnétique () selon l'équation d'induction :
Le rapport entre le second terme du côté droit et le premier terme correspond au nombre de Reynolds magnétique.
Réchauffement par effet de marée[modifier | modifier le code]
Les forces de marée entre les corps célestes en orbite provoquent une friction qui réchauffe l'intérieur de ces corps et contribue à réunir les facteurs de l'effet dynamo, à condition que cet intérieur soit conducteur. Par exemple, les forces de marées subies par les satellites Encelade de Saturne et Io de Jupiter sont suffisantes pour liquéfier l'intérieur de ces astres, même s'ils ne sont pas nécessairement suffisamment conducteurs[8],[9]. Malgré sa petite taille, Mercure a un champ magnétique, car elle possède un noyau liquide conducteur tandis qu'un frottement suffisant résulte de son orbite très elliptique[10]. Une théorie, appuyée par des roches lunaires aimantées, avance que la Lune avait autrefois un champ magnétique[11].
Dynamo cinématique[modifier | modifier le code]


Dans la théorie de la dynamo cinématique, plutôt que d'être une variable dynamique, le champ de vitesse est déterminé. Elle est établie en utilisant les équations de Maxwell conjuguées à la loi d'Ohm.
La caractéristique la plus intéressante de la théorie de la dynamo cinématique est qu'elle peut être utilisée pour tester si un champ de vitesse est ou n'est pas capable de créer un effet dynamo.
Dynamo non linéaire[modifier | modifier le code]
L'approximation cinématique devient invalide lorsque le champ magnétique devient assez fort pour influer sur les mouvements fluides. Dans ce cas, le champ de vitesse est affecté par la force de Lorentz et l'équation d'induction n'est plus linéaire. Dans cette situation, des modèles numériques sont utilisés pour simuler des dynamos entièrement non linéaires.
Notes et références[modifier | modifier le code]
- (en) J. Larmor, « How could a rotating body such as the Sun become a magnet? », Reports of the British Association, vol. 87, , p. 159-160
- (en) J. Larmor, « Possible rotational origin of magnetic fields of sun and earth », Electrical Review, vol. 85, , p. 412ff
- (en) Mary Jo Nye, « Temptations of theory, strategies of evidence: P. M. S. Blackett and the earth's magnetism, 1947–52 », The British Journal for the History of Science, vol. 32, no 1, , p. 69–92 (DOI 10.1017/S0007087498003495)
- Merrill, McElhinny et McFadden 1996, p. 17.
- (en) Ataru Sakuraba et Paul H. Roberts, « Generation of a strong magnetic field using uniform heat flux at the surface of the core », Nature Geoscience, Nature Publishing Group, vol. 2, , p. 802–805 (DOI 10.1038/ngeo643, Bibcode 2009NatGe...2..802S, résumé)
- (en) Bruce Buffett, « Geodynamo: A matter of boundaries », Nature Geoscience, Nature Publishing Group, vol. 2, , p. 741–742 (DOI 10.1038/ngeo673, Bibcode 2009NatGe...2..741B, résumé)
- (en) E. Pallé, The Earth as a Distant Planet : A Rosetta Stone for the Search of Earth-Like Worlds (Astronomy and Astrophysics Library), Berlin, Springer, , 422 p. (ISBN 978-1-4419-1683-9 et 1-4419-1683-0, lire en ligne)
- (en) Bill Steigerwald, « Saturn's Icy Moon May Keep Oceans Liquid with Wobble », NASA,
- (en) Nikki Cassis, « Geologic map of Jupiter’s moon Io details an otherworldly volcanic surface », Astrogeology Science Center,
- (en) « Mercury’s Surprising Core and Landscape Curiosities », MESSENGER, Carnegie Institution for Science,
- (en) Tim Stevens, « Ancient lunar dynamo may explain magnetized moon rocks », University of California, 0 novembre 2011
Bibliographie[modifier | modifier le code]
- (en) Ronald T. Merrill, Michael W. McElhinny et Phillip L. McFadden, The Magnetic Field of the Earth : Paleomagnetism, the Core, and the Deep Mantle, Academic Press, , 531 p. (ISBN 978-0-12-491246-5, lire en ligne)



