Algorithme du lièvre et de la tortue

L'algorithme du lièvre et de la tortue, également connu sous le nom d'algorithme de détection de cycle de Floyd, est un algorithme pour détecter un cycle dans une suite récurrente engendrée par une certaine fonction f définie d'un ensemble fini S dans lui-même. Alors qu'un algorithme naïf consisterait à stocker chaque élément de la suite et, à chaque étape, de vérifier si le nouvel élément fait partie des éléments déjà rencontrés, l'algorithme de Floyd, lui, utilise un espace constant. L'algorithme a un bon comportement quand la fonction f a un comportement pseudo-aléatoire, et celui-ci peut être analysé par le paradoxe des anniversaires.

L'algorithme est sommairement décrit en 1969 par Donald Knuth dans un exercice du volume 2 de The Art of Computer Programming^[1] et attribué à Robert Floyd sans autre précision. Il est aussi décrit dans la note 3.8 de^[2] et est aussi attribué à Robert W. Floyd. Contrairement à ce que l'on trouve parfois, il n'est pas décrit dans un article de 1967^[3] de ce dernier^[4].

L'algorithme rho de Pollard pour la décomposition en nombres premiers de même que celui pour le calcul du logarithme discret utilisent tous deux l'algorithme de détection de cycle de Floyd, pour des suites pseudo-aléatoires particulières.

Suite ultimement périodique[modifier | modifier le code]

La suite dessinée ressemble à la lettre grecque rho.

Soit $f\colon S\rightarrow S$ une fonction, et S un ensemble fini de cardinal n. On considère la suite $(a_{i})$ définie par $a_{0}\in S$ et $a_{i+1}=f(a_{i})$ . Cette suite possède un cycle, car le nombre de ses valeurs possibles est majoré par n. Knuth dit que la suite est ultimement périodique^[1] , cela signifie que les valeurs

a₀, a₁, … a_λ, … a_λ+μ-1

sont distinctes et a_n+μ = a_n pour tout n ≥ λ (μ est la longueur du cycle et λ le nombre d'éléments à l'extérieur du cycle).

La suite dessinée ressemble à la lettre grecque ρ, comme montré sur la figure ci-contre. Si l'on parvient à trouver deux indices i < j avec $a_{i}=a_{j}$ alors j-i est un multiple de la longueur du cycle^[2].

Principe[modifier | modifier le code]

L'algorithme de Floyd de détection de cycle repose sur la propriété suivante : si la suite admet un cycle, alors il existe un indice m avec $a_{m}=a_{2m}$ et λ ≤ m ≤ λ+μ. Ainsi, l'algorithme consiste à parcourir la séquence simultanément à deux vitesses différentes : à vitesse 1 pour la tortue et à vitesse 2 pour le lièvre. Autrement dit, l'algorithme inspecte les couples^[2] :

(a₁, a₂), (a₂, a₄), (a₃, a₆), (a₄, a₈), etc.

L'algorithme trouve le premier indice m tel que $a_{m}=a_{2m}$ . Dès lors, $2m-m=m$ est un multiple de la longueur du cycle μ.

Pour déterminer la valeur exacte de μ, il suffit de refaire tourner l'algorithme à partir de m+1, jusqu'à trouver un autre nombre $m_{1}$ tel que $a_{m_{1}}=a_{2{m_{1}}}$ . Dès lors on a d'une part $m_{1}\leq m+\mu$ (car on retombe alors sur $a_{m}$ ) et d'autre part μ qui divise $m_{1}-m$ (car il divise $m$ et $m_{1}$ ), donc $\mu =m_{1}-m$ .

Exemple[modifier | modifier le code]

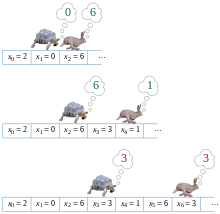
La séquence démarre en bas, monte et emprunte le cycle dans le sens des aiguilles d'une montre (voir figure). Suivant l'algorithme de Floyd, les deux parcours se rencontrent en $a_{6}$ après 6 itérations. Un deuxième tour de l'algorithme amène les deux parcours à se rencontrer après 6 nouvelles itérations, d'où la valeur $\mu =6$ .

Parcours	$t_{1}$	$t_{2}$	$t_{3}$	$t_{4}$	$t_{5}$	$t_{6}$	$t_{7}$	$t_{8}$	$t_{9}$	$t_{10}$	$t_{11}$	$t_{12}$
Lent (tortue)	$a_{1}$	$a_{2}$	$a_{3}$	$a_{4}$	$a_{5}$	$a_{6}$	$a_{7}$	$a_{2}$	$a_{3}$	$a_{4}$	$a_{5}$	$a_{6}$
Rapide (lièvre)	$a_{2}$	$a_{4}$	$a_{6}$	$a_{2}$	$a_{4}$	$a_{6}$	$a_{2}$	$a_{4}$	$a_{6}$	$a_{2}$	$a_{4}$	$a_{6}$

Complexité[modifier | modifier le code]

La complexité en temps peut-être mesurée par le nombre de comparaisons. L'algorithme effectue au minimum λ comparaisons, étant donné que le parcours lent de la séquence doit au moins atteindre le cycle pour rencontrer le parcours rapide. Le nombre maximum de comparaisons est $\lambda +\mu$ , étant donné que le parcours lent ne peut effectuer plus d'un tour du cycle avant d'être rattrapé par le parcours rapide. L'algorithme utilise un espace O(1).

Pseudo-code[modifier | modifier le code]

Trouver l'indice m[modifier | modifier le code]

entrée : une fonction f, une valeur initiale  $a_{0}$ 
sortie : indice m avec a_m = a_2m
détection-cycle-floyd(f,  $a_{0}$ )
          m = 1
          tortue = f( $a_{0}$ )
          lièvre = f(f( $a_{0}$ ))

          tant que tortue != lièvre faire
                m = m + 1
                tortue = f(tortue)
                lièvre = f(f(lièvre))

          renvoyer m

Calcul de la longueur du cycle[modifier | modifier le code]

Si on souhaite obtenir la valeur de $\mu$ , il suffit d'ajouter à la suite le code suivant :

 mu = 0
 répéter
       mu = mu+1
       tortue = f(tortue)
       lièvre = f(f(lièvre))
 tant que tortue != lièvre

Améliorations[modifier | modifier le code]

Brent a amélioré l'algorithme du lièvre et de la tortue^[5]. Il prétend qu'il est 36% plus rapide que l'algorithme du lièvre et de la tortue classique. Il améliore l'algorithme rho de Pollard de 24%.

entrée : une fonction f, valeur initiale a0
sortie : la longueur du cycle, et le nombre d'éléments avant d'atteindre le cycle
brent(f, a0)

    puissance = lam = 1
    tortue = a0
    lièvre = f(a0)
    while tortue != lièvre:
        if puissance == lam:  # on passe à la puissance de deux suivante
            tortue = lièvre
            puissance *= 2
            lam = 0
        lièvre = f(lièvre)
        lam += 1

    # on trouve ici l'indice de la première répétition de longueur λ
    tortue = lièvre = a0
    pour i = 0 à lam-1
            lièvre = f(lièvre)
    # la distance entre le lièvre et la tortue est λ.

    # Maintenant, le lièvre et la tortue bougent à la même vitesse jusqu'à être d'accord
    mu = 0
    tant que tortue != lièvre:
        tortue = f(tortue)
        lièvre = f(lièvre)
        mu += 1
 
    renvoyer lam, mu

Références[modifier | modifier le code]

↑ ^{a et b} Donald E. Knuth, The Art of Computer Programming, vol. II: Seminumerical Algorithms, Addison-Wesley, 1969, p. 7, exercises 6 and 7
↑ ^{a b et c} Handbook of Applied Cryptography, by Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone, p. 125, describes this algorithm and others
↑ (en) R.W. Floyd, « Non-deterministic Algorithms », sur J. ACM, octobre 1967, pp. 636-644
↑ The Hash Function BLAKE, Jean-Philippe Aumasson, Willi Meier, Raphael C.-W. Phan, Luca Henzen (2015), p. 21, footnote 8.
↑ (en) Antoine Joux, Algorithmic Cryptanalysis, CRC Press, 2009, 520 p. (ISBN 978-1-4200-7003-3)

(en) Cet article est partiellement ou en totalité issu de l’article de Wikipédia en anglais intitulé « Floyd's cycle-finding algorithm » (voir la liste des auteurs).

Bibliographie[modifier | modifier le code]

(en) Antoine Joux, Algorithmic Cryptanalysis, CRC Press, 2009, 520 p. (ISBN 978-1-4200-7003-3, présentation en ligne), p. 223-242.

Portail de l'informatique théorique

[knuth-1] {a et b} Donald E. Knuth, The Art of Computer Programming, vol. II: Seminumerical Algorithms, Addison-Wesley, 1969, p. 7, exercises 6 and 7

[:0-2] {a b et c} Handbook of Applied Cryptography, by Alfred J. Menezes, Paul C. van Oorschot, Scott A. Vanstone, p. 125, describes this algorithm and others

[3] (en) R.W. Floyd, « Non-deterministic Algorithms », sur J. ACM, octobre 1967, pp. 636-644

[4] The Hash Function BLAKE, Jean-Philippe Aumasson, Willi Meier, Raphael C.-W. Phan, Luca Henzen (2015), p. 21, footnote 8.

[5] (en) Antoine Joux, Algorithmic Cryptanalysis, CRC Press, 2009, 520 p. (ISBN 978-1-4200-7003-3)

[1]

[2]

[3]

[4]

[5]