Absorbance
L'absorbance mesure la capacité d'un milieu à absorber la lumière qui le traverse. On utilise aussi les termes densité optique, opacité ou extinction selon les domaines avec des expressions mathématiques qui diffèrent légèrement.
En photographie, l'opacité O désigne, dans le cas d'une observation par transmission, l'inverse du coefficient de transmission T[1], alors également nommé transparence, ou, dans le cas d'une observation par réflexion, l'inverse de la réflectance ρ.
En spectrophotométrie, notamment dans le domaine des mesures de concentrations chimiques, l'absorbance A est le logarithme décimal du rapport entre l'intensité énergétique I0 à une longueur d'onde donnée, avant traversée du milieu, et l'intensité énergétique transmise I[2] :
L'absorbance diffère selon la nature de la substance étudiée, selon la longueur d'onde sous laquelle elle est analysée, et selon la concentration de cette substance dans le milieu traversé. Ce milieu peut être solide, liquide ou gazeux, pour autant qu'il soit transparent. Elle est couramment mesurée par un spectrophotomètre. Elle prend théoriquement une valeur entre 0 et l'infini, mais techniquement il n'est pas aisé de mesurer un rapport supérieur à mille. Les spectrophotomètres usuels ne donnent donc pas de valeur d'absorbance supérieure à 3. Pour étudier une substance fortement absorbante, il faut en diminuer l'épaisseur ou la concentration.
En photographie, la densité optique D est équivalente à l'absorbance en spectrométrie, mais toujours mesurée dans le domaine de sensibilité des surfaces sensibles.
Elle est utilisée pour caractériser les filtres colorés, correcteurs de température de couleur ou à densité neutre mais aussi la transparence d'une pellicule photographique développée.
Grandeurs caractéristiques d'atténuation[modifier | modifier le code]
En radiométrie, on définit les quantités suivantes pour un milieu de longueur l et d'indice réfraction n traversé par une lumière d'intensité incidente I0 et d'intensité transmise I.
| Quantité | Expression |
|---|---|
| Chemin optique (m) | |
| Transmittance ou facteur de transmission ou transparence[1] | |
| Opacité[1] | |
| Absorbance[2] | |
| Coefficient d'absorption, absorptivité[3] (m−1) | ou |
| Coefficient d'absorption molaire ou absorptivité molaire[4] (m2⋅mol−1) | ou |
| Densité optique[1] | |
| Épaisseur optique | |
| Atténuation (dB) | |
| Atténuation linéique (dB⋅m−1)[réf. nécessaire] |
Lorsqu'on s'intéresse à la lumière réfléchie par un objet, et non à la lumière qu'il transmet, les définitions ci-dessus s'appliquent toujours en remplaçant la transmittance T par la réflectance ρ.
Par exemple, pour :
- la neige, ρ = 93 % et D = 0,03 ;
- le gris de référence, ρ = 18 % et D = 0,744 ;
- le velours noir, ρ = 0,4 % et D = 2,40.
Opacité et densité optique en photographie[modifier | modifier le code]
Photométrie et prise de vue[modifier | modifier le code]

Dans le domaine de la photographie, les fabricants de filtres renseignent leur documentations techniques :
- avec les transmittances spectrales ou les densités spectrales pour les filtres colorées ;
- avec la densité globale pour les filtres à densité neutre ;
- avec le nombre de diaphragmes qu'il faut ouvrir pour compenser la perte de luminosité de la scène : ce nombre est alors noté stop-value.
| Transmittance T | Opacité O | Densité optique D | Stop-value ΔI |
|---|---|---|---|
| 79 % | 1,3 | 0,1 | 1/3 stop |
| 63 % | 1,6 | 0,2 | 2/3 stop |
| 50 % | 2 | 0,3 | 1 stop |
| 25 % | 4 | 0,6 | 2 stops |
| 12,5 % | 8 | 0,9 | 3 stops |
Dans le dernier cas, le filtre ne laisse passer qu'un huitième de la lumière : le photographe devra, pour maintenir la même exposition lumineuse, soit ouvrir de trois « diaph », soit multiplier par 8 le temps de pose. En photographie numérique, il est aussi possible de multiplier par 8 la sensibilité ISO. En vidéo, on peut ajouter trois fois un gain de 6 dB, soit 18 dB.
Sensitométrie argentique[modifier | modifier le code]
La densité optique est le plus souvent définie à partir de la transmittance[5],[1] :
Dans le cas fréquent d'un négatif ou interpositif destiné à la reproduction, la densité se mesure dans le domaine de sensibilité de la pellicule qui doit reproduire. En noir et blanc, ces surfaces destinées à la reproduction sont la plupart du temps non chromatisées, sensibles uniquement au bleu. En couleurs, on mesure normalement avec des filtres correspondant aux trois couleurs primaires.
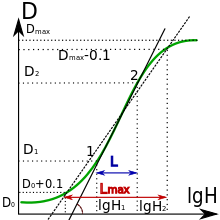
Pour les pellicules photographiques la densité optique après développement dépend du logarithme de l'exposition lumineuse et la relation est représentée sur la courbe caractéristique. La pente de la partie droite de la courbe est d'autant plus élevée que le film est contrasté. Cette pente est appelée le gamma de la pellicule. Il en va de même pour le tirage sur papier photographique.
Lois de l'absorption de la lumière[modifier | modifier le code]
Soit un faisceau de lumière monochromatique qui traverse une couche de matière transparente (comme un morceau de glace par exemple). Une part de l'énergie rayonnante passera à travers cette substance (énergie transmise), mais une partie sera réfléchie et une autre absorbée. La conservation de l'énergie incidente se traduit par la relation : où
- Ii est l'intensité énergétique incidente ;
- Ia est l'intensité énergétique absorbée ;
- Ir est l'intensité énergétique réfléchie ;
- It est l'intensité énergétique transmise.
L'énergie perdue par la réflexion est minimisée en effectuant des mesures en incidence normale (angle pour lequel la réflexion partielle est faible). Elle est prise en compte en comparant l'énergie transmise à celle passant dans un système équivalent (même matériau, même géométrie) mais ne contenant pas la substance à analyser (par exemple une cellule de référence en spectroscopie usuelle). On s'intéressera alors à la relation entre énergie incidente et énergie transmise. Cette relation a été formulée par Pierre Bouguer en 1729. La loi de Bouguer (connue aussi comme la loi de Lambert) consiste en deux parties : la première définit la transmittance, la seconde la variation de l'absorbance en fonction de l'épaisseur de la couche de substance traversée par la lumière.
Loi de Bouguer[modifier | modifier le code]

Comme convenu précédemment, l'énergie transmise par un milieu homogène est proportionnelle à l'énergie appliquée sur celui-ci. Ainsi, l'énergie transmise par celui-ci sera toujours une partie de l'énergie totale appliquée. Ce rapport est défini comme la transmittance T, qui s'exprime donc comme . Pour une substance donnée, avec une épaisseur et une longueur d'onde définies, T est une constante.
Supposons qu'une substance, d'un centimètre d'épaisseur permet à 50 % de l'énergie reçue de la traverser. Autrement dit, sa transmittance vaut 0,5. Si cette lumière obtenue passe par une deuxième couche de même épaisseur, une nouvelle fois seuls 50 % de celle-ci réussiront à passer à travers. Au passage successif par les deux couches, seulement 25 % de l'énergie de la lumière incidente ont été transmis par 2 cm de cette substance (0,5 x 0,5 = 0,52 = 0,25). De même, 3 cm transmettront 12,5 % du total reçu (0,5 x 0,5 x 0,5 = 0,53 = 0,125). Il s'agit donc là d'une progression géométrique : la transmittance ne diminue donc pas d'une manière linéaire quand l'épaisseur augmente, mais exponentielle (voir figure). En conséquence, le logarithme de T (log T) diminue linéairement en fonction de l'épaisseur[a].
Le changement subi par l'énergie rayonnante en fonction de la longueur du trajet optique traversé , est défini par la relation :,où est une constante de proportionnalité.
En intégrant cette équation, on obtient : ,d'où :.
Pour les chimistes, on remplace le logarithme népérien par le logarithme décimal en divisant le facteur par ln 10 ≈ 2,303 et en incorporant le résultat dans une nouvelle constante notée :,donc :.
On définit maintenant l'absorbance par :,où est le coefficient d'absorption ou l'absorptivité du milieu, exprimé en m−1 ou cm−1.
Dans une solution, on peut diviser le coefficient d'absorption par la concentration molaire des entités contenues dans le volume traversé par un faisceau lumineux : , où
- ε est le coefficient d'absorption molaire ou l'absorptivité molaire de l'entité en solution, exprimée en L⋅mol−1⋅cm−1 ;
- c est la concentration molaire, exprimée en mol⋅L−1 ou en mol⋅m−3.
Le coefficient d'absorption molaire dépend de la nature du corps absorbant, de la longueur d'onde choisie et de la température.
Loi de Beer-Lambert[modifier | modifier le code]
Pour plus de détails, voir l'article Loi de Beer-Lambert
Utilisant le même raisonnement que celui de la loi de Bouguer, August Beer propose en 1852 une équation reliant l'absorbance et la transmittance à la concentration d'une substance en solution. La loi est énoncée de la manière suivante : .
L'absorptivité a peut être remplacée dans l'équation par le coefficient d'extinction molaire ε comme défini précédemment. Alors, par la combinaison des deux équations, on obtient la loi de Beer–Bouguer mieux connue comme la loi de Beer–Lambert : .
La mesure de l'absorbance se fait grâce à un spectrophotomètre. l est la longueur du chemin optique traversé par la lumière dans la solution en cm. En pratique, cette longueur correspond à l'épaisseur de la cuve de mesure (généralement prise de 1 cm).
Cette loi permet aux chimistes de déterminer la concentration inconnue d'un ou plusieurs éléments dans une solution donnée. Toutefois, cette proportionnalité entre la concentration et l'absorbance ne serait plus applicable pour c > 0,01 mol⋅L−1 (car le phénomène de réflexion n'est plus négligeable).
Colorimétrie[modifier | modifier le code]
Si un élément n'absorbe pas assez la lumière pour effectuer des mesures correctes, on le fait réagir avec un autre élément pour que le produit de la réaction affiche une couleur bien visible. L'intensité de la coloration obtenue est proportionnelle à la concentration réelle.
Turbidimétrie[modifier | modifier le code]
La turbidimétrie se base sur un système de détection optique qui mesure la turbidité, c'est-à-dire la concentration de très petites particules en suspension dans une solution (mg⋅L−1). La lumière transmise à travers un milieu turbide dépend de la concentration en objets diffusants et de leurs sections efficaces d’extinction, donc de leurs tailles, leurs formes, leurs indices de réfraction, et de la longueur d’onde considérée. Pour de faibles concentrations, l'intensité transmise peut être déterminée par la loi de Beer–Lambert. La mesure de l'intensité transmise permet ainsi, de remonter à la distribution de taille et à la concentration des particules absorbantes.
Notes et références[modifier | modifier le code]
Bibliographie[modifier | modifier le code]
- (en) Mahmoud M. Abdel-Monem et James G. Henkel (ill. Richard D. Heaney), Essentials of drug product quality : concepts and methodology, Saint Louis, The Mosby Company, , 274 p. (ISBN 978-0-801-60031-9, OCLC 3542228), p. 30-133.
- IUPAC, Compendium of Chemical Terminology : The Gold Book, , 2e éd. (ISBN 0-86542-684-8, lire en ligne)
- René Bouillot, Cours de photographie : Technique et pratique, Paris, Dunod, (ISBN 2-10-000325-9), p. 89
- José-Philippe Pérez, Optique : Fondements et applications, Paris, Dunod, coll. « Enseignement de la physique », , 7e éd. (ISBN 2-10-048497-4)
Références[modifier | modifier le code]
- En pratique les astronomes mesurent durant une nuit d'observation une même étoile à différentes distances zénithales définies par l'angle θ. Les magnitudes portées en fonction de l'épaisseur d'atmosphère traversée, proportionnelle à (1/cosθ), s'alignent sur une droite, en tolérant les écarts dus aux erreurs de mesure et aux variations d'absorption atmosphérique au fil des heures. Cette droite s'appelle la droite de Bouguer. L'ordonnée à l'origine de cette droite (pour un cosinus virtuellement infini, dont l'inverse vaut zéro) donne la valeur de la magnitude hors atmosphère.
- Bouillot 1991, p. 89.
- IUPAC 1997, p. 9.
- IUPAC 1997, p. 13.
- IUPAC 1997, p. 947.
- Pérez 2004, p. 183.
- Cet article est partiellement ou en totalité issu de l'article intitulé « Opacité » (voir la liste des auteurs).
- Cet article est partiellement ou en totalité issu de l'article intitulé « Densité optique » (voir la liste des auteurs).




























